Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 144849 by Dwaipayan Shikari last updated on 29/Jun/21

$${\int }_0^2\frac{1}{e^{{\left\{x\right\}}^2}+1}dx\left\{x\right\}isfractionalpartofx$$

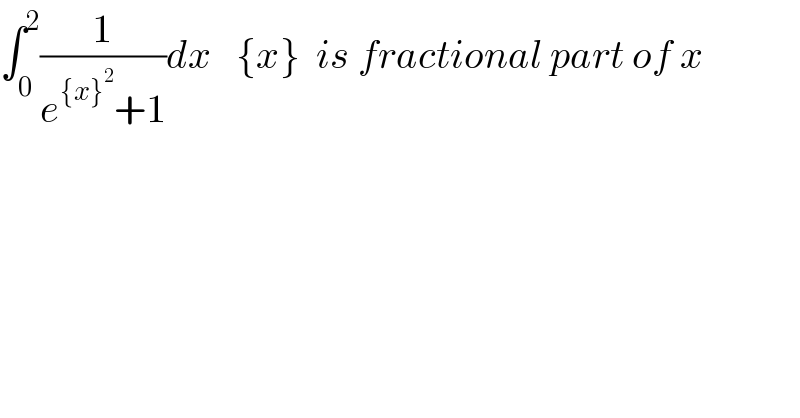
Answered by mathmax by abdo last updated on 29/Jun/21

$$\mathrm{\Phi }={\int }_0^2\frac{\mathrm{dx}}{{\mathrm{e}}^{{\left\{\mathrm{x}\right\}}^2}+1}\mathrm{we}\mathrm{have}\mathrm{x}=\left[\mathrm{x}\right]+\left\{\mathrm{x}\right\}\Rightarrow \left\{\mathrm{x}\right\}=\mathrm{x}-\left[\mathrm{x}\right]\Rightarrow$$$$\mathrm{\Phi }={\int }_0^1\frac{\mathrm{dx}}{{\mathrm{e}}^{{(\mathrm{x}-\left[\mathrm{x}\right])}^2}+1}+{\int }_1^2\frac{\mathrm{dx}}{{\mathrm{e}}^{{(\mathrm{x}-\left[\mathrm{x}\right])}^2}+1}$$$$={\int }_0^1\frac{\mathrm{dx}}{1+{\mathrm{e}}^{{\mathrm{x}}^2}}+{\int }_1^2\frac{\mathrm{dx}}{1+{\mathrm{e}}^{{(\mathrm{x}-1)}^2}}(\to \mathrm{x}-1=\mathrm{t})$$$$={\int }_0^1\frac{\mathrm{dx}}{1+{\mathrm{e}}^{{\mathrm{x}}^2}}+{\int }_0^1\frac{\mathrm{dt}}{1+{\mathrm{e}}^{{\mathrm{t}}^2}}=2{\int }_0^1\frac{\mathrm{dx}}{1+{\mathrm{e}}^{{\mathrm{x}}^2}}$$$${\int }_0^1\frac{\mathrm{dx}}{1+{\mathrm{e}}^{{\mathrm{x}}^2}}={\int }_0^1\frac{{\mathrm{e}}^{-{\mathrm{x}}^2}}{1+{\mathrm{e}}^{-{\mathrm{x}}^2}}\mathrm{dx}={\int }_0^1{\mathrm{e}}^{-{\mathrm{x}}^2}\sum _{\mathrm{n}=0}^{\mathrm{\infty }}{\mathrm{e}}^{-{\mathrm{nx}}^2}\mathrm{dx}$$$$=\sum _{\mathrm{n}=0}^{\mathrm{\infty }}{\int }_0^1{\mathrm{e}}^{-(\mathrm{n}+1){\mathrm{x}}^2}\mathrm{dx}{=}_{\sqrt{\mathrm{n}+1}\mathrm{x}=\mathrm{z}}\sum _{\mathrm{n}=0}^{\mathrm{\infty }}{\int }_0^{\sqrt{\mathrm{n}+1}}{\mathrm{e}}^{-{\mathrm{z}}^2}\frac{\mathrm{dz}}{\mathrm{n}+1}$$$$\mathrm{\Phi }=\sum _{\mathrm{n}=0}^{\mathrm{\infty }}\frac{1}{\mathrm{n}+1}{\int }_0^{\sqrt{\mathrm{n}+1}}{\mathrm{e}}^{-{\mathrm{z}}^2}\mathrm{dz}$$

Commented by mathmax by abdo last updated on 29/Jun/21

$$\mathrm{\Phi }=\sum _{\mathrm{n}=0}^{\mathrm{\infty }}\frac{2}{\mathrm{n}+1}{\int }_0^{\sqrt{\mathrm{n}+1}}{\mathrm{e}}^{-{\mathrm{z}}^2}\mathrm{dz}$$

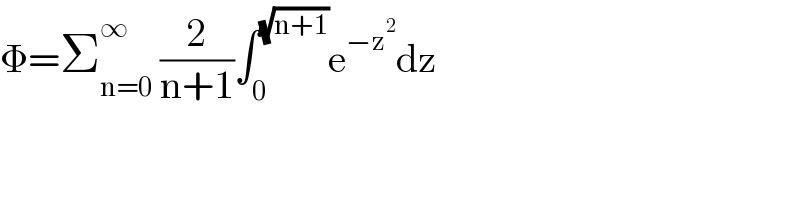
Commented by Dwaipayan Shikari last updated on 29/Jun/21

$$Thankssir$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com