
Question and Answers Forum
Question Number 11436 by @ANTARES_VY last updated on 26/Mar/17
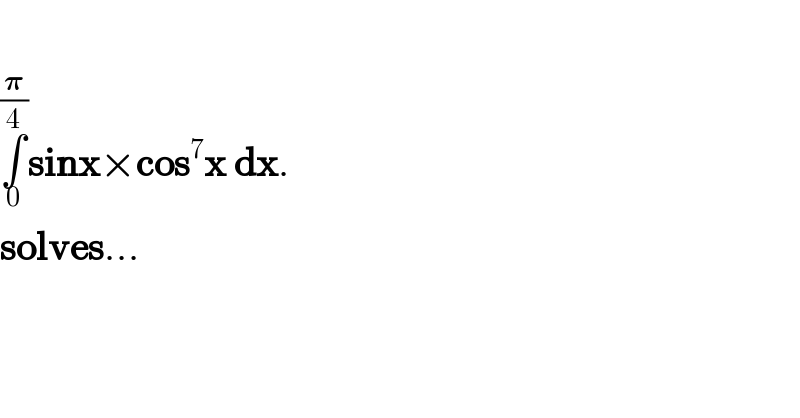
Commented by FilupS last updated on 26/Mar/17
![let u=cos(x) ∴ du=−sin(x)dx ∴∫_0 ^( π/4) sin(x)cos^7 (x)dx=−∫_(x=0) ^( x=π/4) u^7 du −∫_(x=0) ^( x=π/4) u^7 du=−[(1/8)u^8 ]_(x=0) ^(x=π/4) =−(1/8)[cos^8 (x)]_(x=0) ^(x=π/4) =−(1/8)(cos^8 ((π/4))−cos^8 (0)) =−(1/8)(((1/(√2)))^8 −1) =−(1/8)(2^(−(1/2)×8) −1) =−(1/8)(2^(−4) −1) =−(1/2^3 )((1/2^4 )−1) =−((1/2^7 )−(1/2^3 )) =−((1/2^7 )−(2^4 /2^7 )) =−(((1−2^4 )/2^7 )) =((2^4 −1)/2^7 ) =((15)/(128))](Q11442.png)
| ||
Question and Answers Forum | ||
Question Number 11436 by @ANTARES_VY last updated on 26/Mar/17 | ||
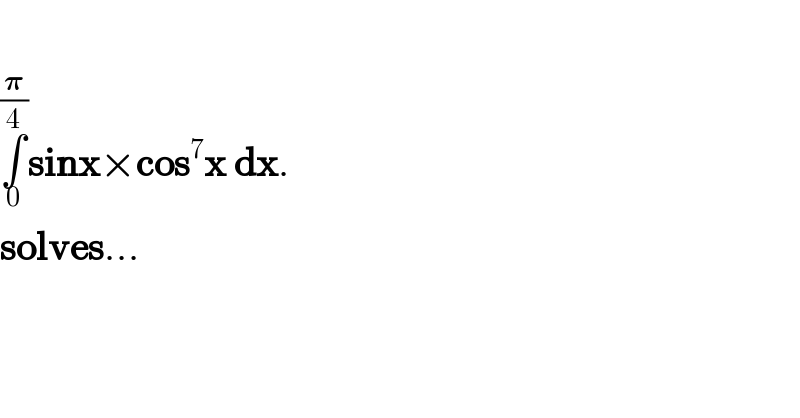 | ||
Commented by FilupS last updated on 26/Mar/17 | ||
![let u=cos(x) ∴ du=−sin(x)dx ∴∫_0 ^( π/4) sin(x)cos^7 (x)dx=−∫_(x=0) ^( x=π/4) u^7 du −∫_(x=0) ^( x=π/4) u^7 du=−[(1/8)u^8 ]_(x=0) ^(x=π/4) =−(1/8)[cos^8 (x)]_(x=0) ^(x=π/4) =−(1/8)(cos^8 ((π/4))−cos^8 (0)) =−(1/8)(((1/(√2)))^8 −1) =−(1/8)(2^(−(1/2)×8) −1) =−(1/8)(2^(−4) −1) =−(1/2^3 )((1/2^4 )−1) =−((1/2^7 )−(1/2^3 )) =−((1/2^7 )−(2^4 /2^7 )) =−(((1−2^4 )/2^7 )) =((2^4 −1)/2^7 ) =((15)/(128))](Q11442.png) | ||