
Question and Answers Forum
Question Number 85346 by naka3546 last updated on 21/Mar/20
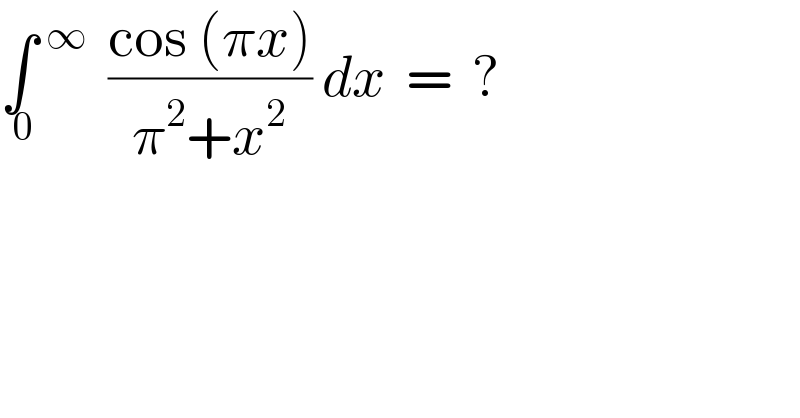
Commented by abdomathmax last updated on 21/Mar/20
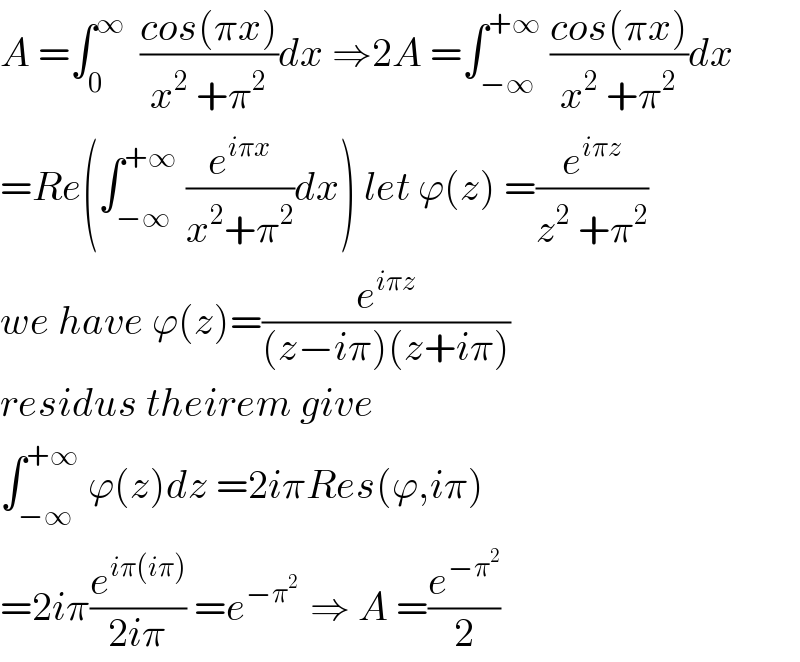
Answered by M±th+et£s last updated on 21/Mar/20
![f(p)=∫_0 ^∞ ((cos(pπx))/(π^2 +x^2 )) dx⇒⇒⇒⌊(f(p))=∫_0 ^∞ ∫_0 ^∞ ((cos(pπx))/(π^2 +x^2 )) dx dp =∫_0 ^∞ (1/(π^2 +x^2 ))∫_0 ^∞ e^(−ps) cos(pπx) dx dp =∫_0 ^∞ (1/((π^2 +x^2 )))((s/(s^2 +π^2 x^2 )))dx =(s/(s−π^4 ))∫_0 ^∞ ((s^2 +π^2 x^2 −π^4 −π^2 x^2 )/((π^2 +x^2 )(s^2 +π^2 x^2 ))) dx (s/(s^2 −π^4 ))∫((1/(π^2 +x^2 ))−(π^2 /(s^2 +π^2 x^2 )))dx (s/(s^2 −π^4 ))[(1/π)tan^(−1) (x/π) −(π/s)tan^(−1) ((πx)/s)]_0 ^∞ (s/(s^2 −π^4 ))[(1/2)−(π^2 /(2s))] (s/(s^2 −π^4 ))(((s−π^2 )/(2s)))=(1/(2(s+π^2 ))) f(p)=⌊^(−1) ((1/(s+π^2 ))) =(1/2)e^(−π^2 )](Q85419.png)
| ||
Question and Answers Forum | ||
Question Number 85346 by naka3546 last updated on 21/Mar/20 | ||
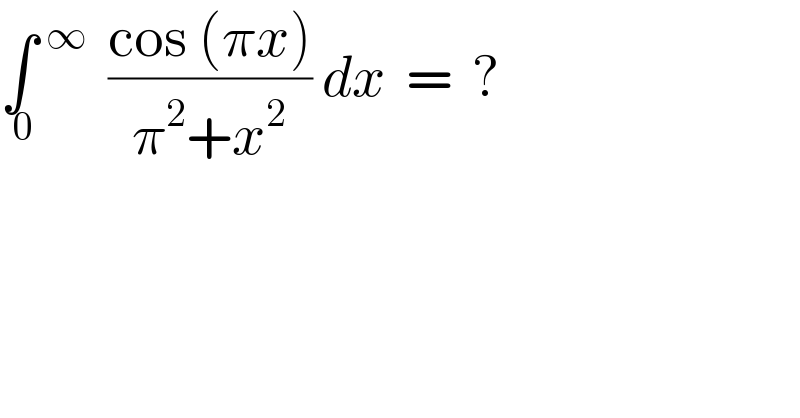 | ||
Commented by abdomathmax last updated on 21/Mar/20 | ||
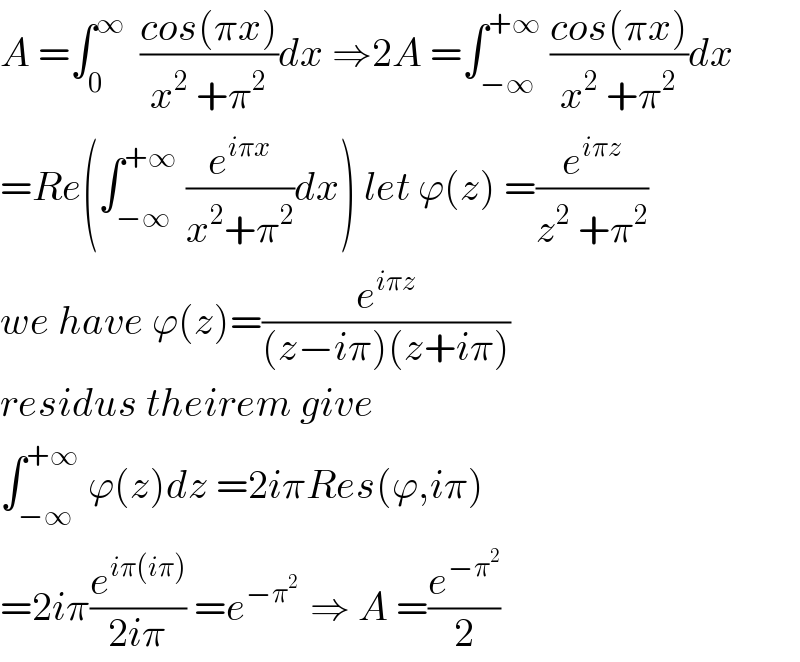 | ||
Answered by M±th+et£s last updated on 21/Mar/20 | ||
![f(p)=∫_0 ^∞ ((cos(pπx))/(π^2 +x^2 )) dx⇒⇒⇒⌊(f(p))=∫_0 ^∞ ∫_0 ^∞ ((cos(pπx))/(π^2 +x^2 )) dx dp =∫_0 ^∞ (1/(π^2 +x^2 ))∫_0 ^∞ e^(−ps) cos(pπx) dx dp =∫_0 ^∞ (1/((π^2 +x^2 )))((s/(s^2 +π^2 x^2 )))dx =(s/(s−π^4 ))∫_0 ^∞ ((s^2 +π^2 x^2 −π^4 −π^2 x^2 )/((π^2 +x^2 )(s^2 +π^2 x^2 ))) dx (s/(s^2 −π^4 ))∫((1/(π^2 +x^2 ))−(π^2 /(s^2 +π^2 x^2 )))dx (s/(s^2 −π^4 ))[(1/π)tan^(−1) (x/π) −(π/s)tan^(−1) ((πx)/s)]_0 ^∞ (s/(s^2 −π^4 ))[(1/2)−(π^2 /(2s))] (s/(s^2 −π^4 ))(((s−π^2 )/(2s)))=(1/(2(s+π^2 ))) f(p)=⌊^(−1) ((1/(s+π^2 ))) =(1/2)e^(−π^2 )](Q85419.png) | ||
| ||