∫_( 0) ^(π/2) (1/(1+tan x)) dx =


Question and Answers Forum

All Questions Topic List
UNKNOWN Questions
Previous in All Question Next in All Question
Previous in UNKNOWN Next in UNKNOWN
Question Number 64333 by Chi Mes Try last updated on 16/Jul/19

$\underset{0}{\int^{π / 2}} \frac{1}{1 + \tan x} d x =$
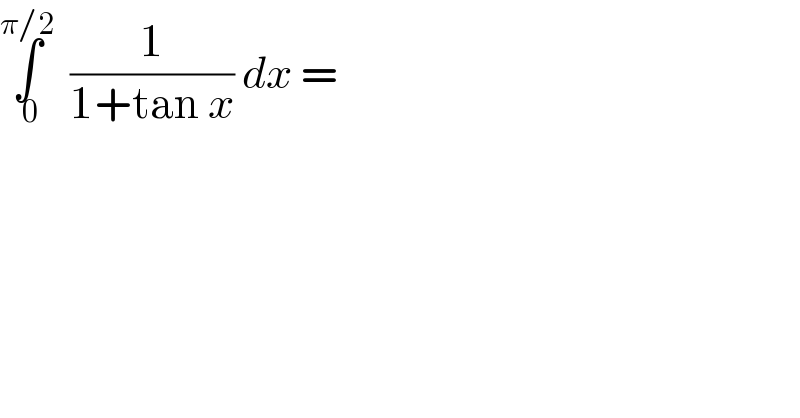
Commented by mathmax by abdo last updated on 16/Jul/19

$l e t I = \int_{0}^{\frac{π}{2}} \frac{d x}{1 + t a n x} c h a n g e m e n t t a n x = t g i v e$ $I = \int_{0}^{+ \infty} \frac{d t}{(1 + t^{2}) (1 + t)} l e t d e c o m p o s e F (t) = \frac{1}{(t + 1) (t^{2} + 1)}$ $F (t) = \frac{a}{t + 1} + \frac{b t + c}{t^{2} + 1}$ $a = {l i m}_{t \to - 1} (t + 1) F (t) = \frac{1}{2}$ ${l i m}_{t \to + \infty} t F (t) = 0 = a + b \Rightarrow b = - \frac{1}{2} \Rightarrow F (t) = \frac{1}{2 (t + 1)} + \frac{- \frac{1}{2} t + c}{t^{2} + 1}$ $F (0) = 1 = \frac{1}{2} + c \Rightarrow c = \frac{1}{2} \Rightarrow F (t) = \frac{1}{2 (t + 1)} - \frac{1}{2} \frac{t - 1}{t^{2} + 1} \Rightarrow$ $I = \int_{0}^{\infty} (\frac{1}{2 (t + 1)} - \frac{1}{4} \frac{2 t}{t^{2} + 1}) d t + \frac{1}{2} \int_{0}^{\infty} \frac{d t}{t^{2} + 1}$ $= \frac{1}{2} {[l n ∣ t + 1 ∣ - \frac{1}{2} l n (t^{2} + 1)]}_{0}^{+ \infty} + \frac{π}{4}$ $= \frac{1}{2} {[l n ∣ \frac{t + 1}{\sqrt{t^{2} + 1}} ∣]}_{0}^{+ \infty} + \frac{π}{4} = 0 + \frac{π}{4} \Rightarrow I = \frac{π}{4} .$
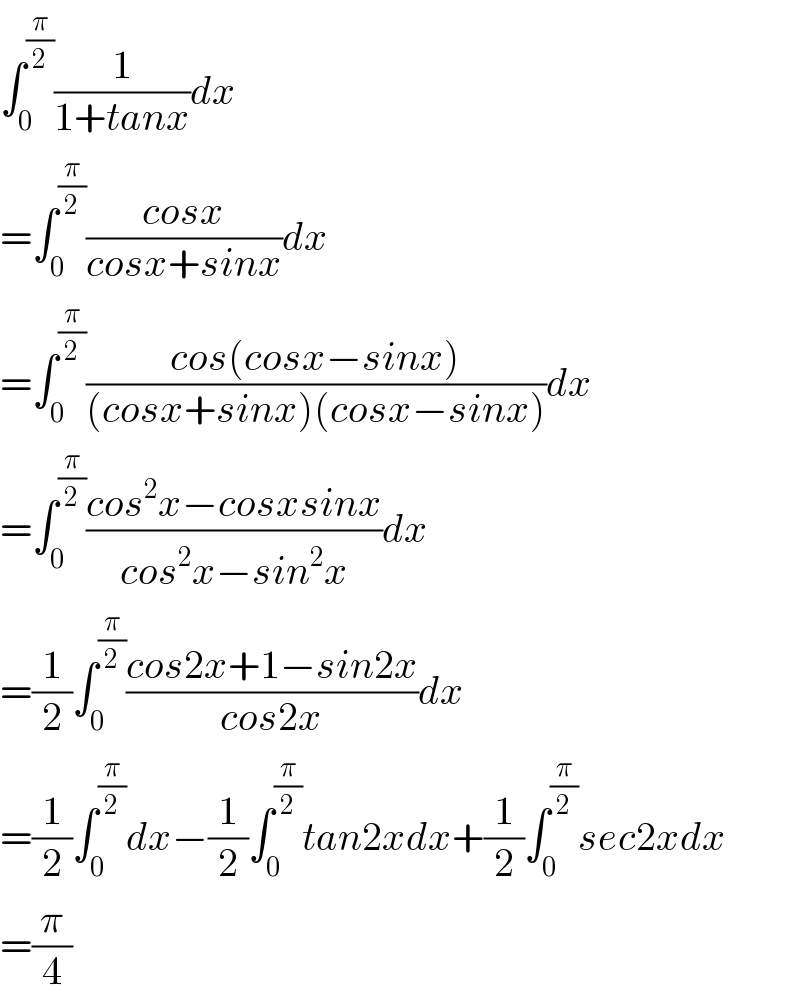
Commented by Tony Lin last updated on 17/Jul/19

$\int_{0}^{\frac{π}{2}} \frac{1}{1 + t a n x} d x$ $= \int_{0}^{\frac{π}{2}} \frac{c o s x}{c o s x + s i n x} d x$ $= \int_{0}^{\frac{π}{2}} \frac{c o s (c o s x - s i n x)}{(c o s x + s i n x) (c o s x - s i n x)} d x$ $= \int_{0}^{\frac{π}{2}} \frac{{c o s}^{2} x - c o s x s i n x}{{c o s}^{2} x - {s i n}^{2} x} d x$ $= \frac{1}{2} \int_{0}^{\frac{π}{2}} \frac{c o s 2 x + 1 - s i n 2 x}{c o s 2 x} d x$ $= \frac{1}{2} \int_{0}^{\frac{π}{2}} d x - \frac{1}{2} \int_{0}^{\frac{π}{2}} t a n 2 x d x + \frac{1}{2} \int_{0}^{\frac{π}{2}} s e c 2 x d x$ $= \frac{π}{4}$
	Answered by Rio Michael last updated on 16/Jul/19

	$b e g i n w i t h$ $\int \frac{1}{1 + t a n x} d x$ $I = \int \frac{1}{1 + t a n x} d x u s e t h e s u b s t i t u t i o n u = t a n x$ $I = \int \frac{1}{(1 + u^{2}) (1 + u)} d u$ $I = \frac{1}{2} \int (\frac{1}{1 + u^{2}} + \frac{1}{1 + u}) d u$ $I = \frac{1}{2} \int (\frac{1}{1 + u^{2}} - \frac{1}{2} \frac{2 u}{1 + u^{2}} + \frac{1}{1 + u}) d u$ $I = \frac{1}{2} (a r c t a n u - \frac{1}{2} l n (1 + u^{2}) + l n (1 + u))$ $I = ⌈ \frac{1}{2} (x - l n (s e c x) + l n (1 + t a n x)) ⌉_{0}^{\frac{π}{2}}$ $I = \frac{1}{2} (\frac{π}{2} + l n (s i n \frac{π}{2} + c o s \frac{π}{2})) = \frac{π}{4}$
	Answered by Tanmay chaudhury last updated on 17/Jul/19

	$I = \int_{0}^{\frac{π}{2}} \frac{c o s x}{c o s x + s i n x} d x$ $= \int_{0}^{\frac{π}{2}} \frac{c o s (\frac{π}{2} - x)}{c o s (\frac{π}{2} - x) + s i n (\frac{π}{2} - x)} d x$ $= \int_{0}^{\frac{π}{2}} \frac{s i n x}{s i n x + c o x} d x$ $2 I = \int_{0}^{\frac{π}{2}} \frac{c o s x}{s i n x + c o s x} + \frac{s i n x}{c o s x + s i n x} d x$ $2 I = \int_{0}^{\frac{π}{2}} d x$ $I = \frac{π}{4}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum