
Question and Answers Forum
Question Number 144530 by EDWIN88 last updated on 26/Jun/21
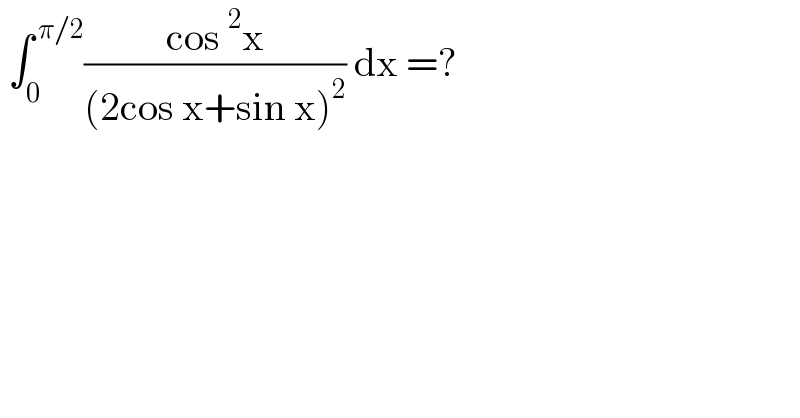
Answered by mathmax by abdo last updated on 26/Jun/21

Answered by Ar Brandon last updated on 26/Jun/21
![I=∫_0 ^(π/2) ((cos^2 x)/((2cosx+sinx)^2 ))dx=∫_0 ^(π/2) (dx/((2+tanx)^2 )) =∫_0 ^∞ ((2dt)/((2+t)^2 (1+t^2 )))=2∫_0 ^∞ (dt/((t+2)^2 (t^2 +1))) =2∫_0 ^∞ ((4/(25))∙(1/(t+2))+(1/5)∙(1/((t+2)^2 ))−(1/(25))∙((4t−3)/(t^2 +1)))dt =2[(4/(25))ln(t+2)−(1/5)∙(1/(t+2))−(2/(25))ln(t^2 +1)+(3/(25))arctan(t)]_0 ^∞ =[(4/(25))ln(((t^2 +2t+2)/(t^2 +1)))−(2/(5(t+2)))+(6/(25))arctan(t)]_0 ^∞ =−(4/(25))ln(2)+(1/5)+((3π)/(25))=(4/(25))ln((1/2))+(1/5)+((3π)/(25))](Q144604.png)
Commented by Ar Brandon last updated on 26/Jun/21
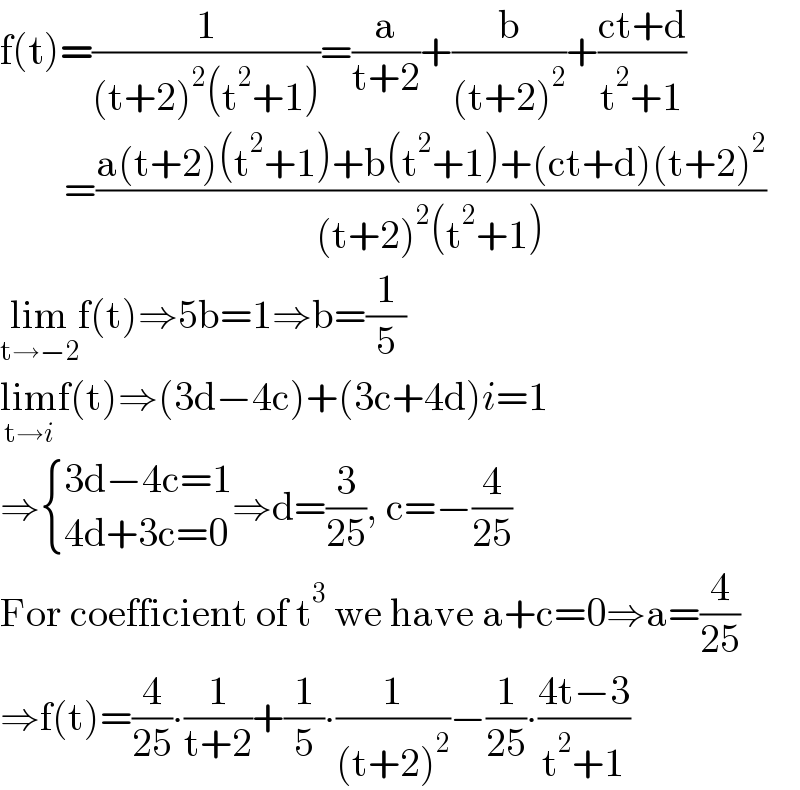
| ||
Question and Answers Forum | ||
Question Number 144530 by EDWIN88 last updated on 26/Jun/21 | ||
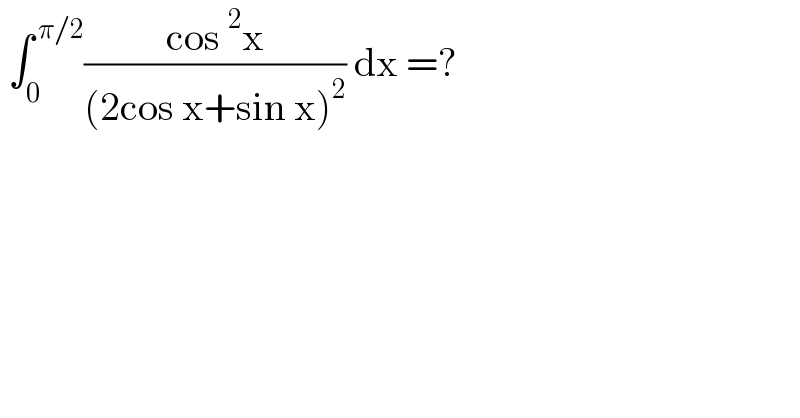 | ||
Answered by mathmax by abdo last updated on 26/Jun/21 | ||
 | ||
| ||
Answered by Ar Brandon last updated on 26/Jun/21 | ||
![I=∫_0 ^(π/2) ((cos^2 x)/((2cosx+sinx)^2 ))dx=∫_0 ^(π/2) (dx/((2+tanx)^2 )) =∫_0 ^∞ ((2dt)/((2+t)^2 (1+t^2 )))=2∫_0 ^∞ (dt/((t+2)^2 (t^2 +1))) =2∫_0 ^∞ ((4/(25))∙(1/(t+2))+(1/5)∙(1/((t+2)^2 ))−(1/(25))∙((4t−3)/(t^2 +1)))dt =2[(4/(25))ln(t+2)−(1/5)∙(1/(t+2))−(2/(25))ln(t^2 +1)+(3/(25))arctan(t)]_0 ^∞ =[(4/(25))ln(((t^2 +2t+2)/(t^2 +1)))−(2/(5(t+2)))+(6/(25))arctan(t)]_0 ^∞ =−(4/(25))ln(2)+(1/5)+((3π)/(25))=(4/(25))ln((1/2))+(1/5)+((3π)/(25))](Q144604.png) | ||
| ||
Commented by Ar Brandon last updated on 26/Jun/21 | ||
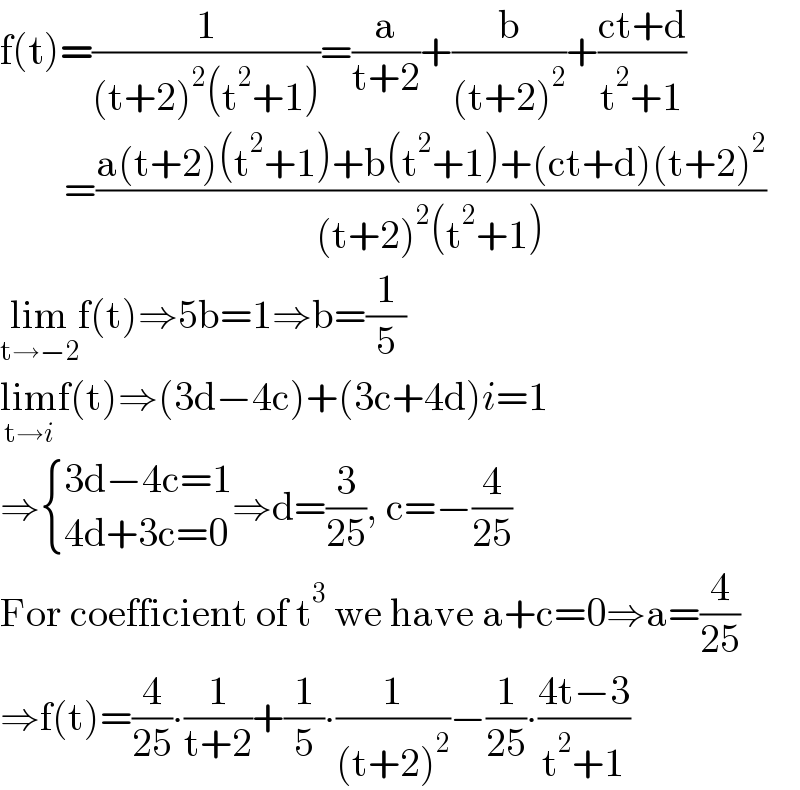 | ||