Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 113821 by 675480065 last updated on 15/Sep/20

$${\int }_0^{\frac{\pi }{2}}\ln (2-\mathrm{sinx})\mathrm{dx}$$

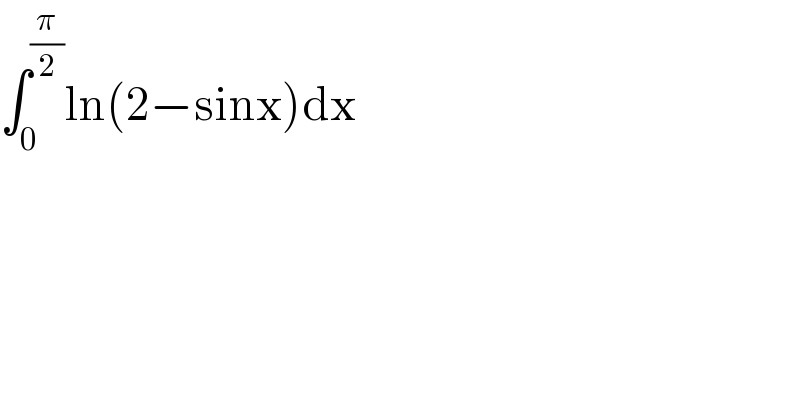
Commented by Dwaipayan Shikari last updated on 15/Sep/20

$$I\left(a\right)={\int }_0^{\frac{\pi }{2}}log(2+asinx)dx$$$$I^{\prime }\left(a\right)={\int }_0^{\frac{\pi }{2}}\frac{sinx}{2+asinx}dx$$$$I^{\prime }\left(a\right)=\frac{1}{a}{\int }_0^{\frac{\pi }{2}}1-\frac{2}{2+asinx}$$$$I^{\prime }\left(a\right)=\frac{\pi }{2a}-2{\int }_0^{\frac{\pi }{2}}\frac{1}{2+asinx}dx$$$$I^{\prime }\left(a\right)=\frac{\pi }{2a}-4{\int }_0^{\frac{\pi }{2}}\frac{1}{2+\frac{2at}{1+t^2}}.\frac{1}{1+t^2}dt(tan\frac{x}{2}=t)$$$$I^{\prime }\left(a\right)=\frac{\pi }{2a}-4{\int }_0^1\frac{1}{2+2t^2+2at}dt$$$$I^{\prime }\left(a\right)=\frac{\pi }{2a}-2{\int }_0^1\frac{1}{{(t+\frac{a}{2})}^2+1-\frac{a^2}{4}}dt$$$$I^{\prime }\left(a\right)=\frac{\pi }{2a}-2\frac{1}{\sqrt{1-\frac{a^2}{4}}}.{\left[{tan}^{-1}\frac{2t+a}{\sqrt{4-a^2}}\right]}_0^1$$$$I\left(a\right)=\frac{\pi }{2}log\left(a\right)-\int \frac{4}{\sqrt{4-a^2}}({tan}^{-1}\sqrt{\frac{2+a}{2-a}}-{tan}^{-1}\frac{a}{\sqrt{4-a^2}})....$$$$.....$$

Answered by mathdave last updated on 15/Sep/20

$$solution$$$$let$$$$A={\int }_0^{\frac{\pi }{2}}\ln \left[2(1-\frac{1}{2}\sin x)\right]dx=\ln 2{\int }^{\frac{\pi }{2}}dx+{\int }^{\frac{\pi }{2}}(1-\frac{1}{2}\sin x)dx$$$$A=\frac{\pi }{2}\ln 2+{\int }_0^{\frac{\pi }{2}}(1-\frac{1}{2}\sin x)dx$$$$letI={\int }_0^{\frac{\pi }{2}}(1-\frac{1}{2}\sin x)dx.........\left(1\right)$$

Commented by mathdave last updated on 15/Sep/20

Commented by mathdave last updated on 15/Sep/20

Commented by mathdave last updated on 15/Sep/20

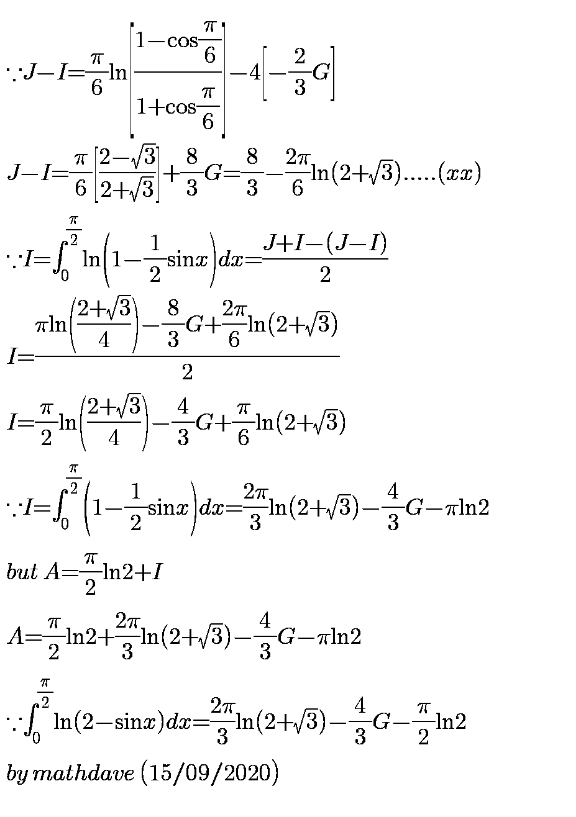
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\mathrm{sir}$$

Answered by Olaf last updated on 15/Sep/20

$$\mathrm{I}={\int }_0^{\frac{\pi }{2}}\ln (2-\sin x)dx$$$$\frac{1}{1-\frac{1}{2}\sin x}=\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{{\sin }^{n}x}{2^n}$$$$\frac{-\frac{1}{2}\cos x}{1-\frac{1}{2}\sin x}=-\frac{1}{2}\underset{n=0}{\sum ^{\mathrm{\infty }}}\cos x\frac{{\sin }^{n}x}{2^n}$$$$\ln (1-\frac{1}{2}\sin x)=-\frac{1}{2}\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{{\sin }^{n+1}x}{2^n(n+1)}$$$$\mathrm{I}=\frac{\pi }{2}\ln 2+{\int }_0^{\frac{\pi }{2}}\ln (1-\frac{1}{2}\sin x)dx$$$$\mathrm{I}=\frac{\pi }{2}\ln 2-{\int }_0^{\frac{\pi }{2}}\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{{\sin }^{n+1}x}{2^{n+1}(n+1)}dx$$$$\mathrm{I}=\frac{\pi }{2}\ln 2-{\int }_0^{\frac{\pi }{2}}\underset{n=1}{\sum ^{\mathrm{\infty }}}\frac{{\sin }^{n}x}{n{2}^n}dx$$$$\mathrm{I}=\frac{\pi }{2}\ln 2-\underset{n=1}{\sum ^{\mathrm{\infty }}}\frac{1}{n{2}^n}{\int }_0^{\frac{\pi }{2}}{\sin }^{n}xdx$$$${\mathrm{W}}_n={\int }_0^{\frac{\pi }{2}}{\sin }^{n}xdx\left(\mathrm{Wallis}\right)$$$$\mathrm{I}=\frac{\pi }{2}\ln 2-\underset{n=1}{\sum ^{\mathrm{\infty }}}\frac{{\mathrm{W}}_n}{n{2}^n}...$$

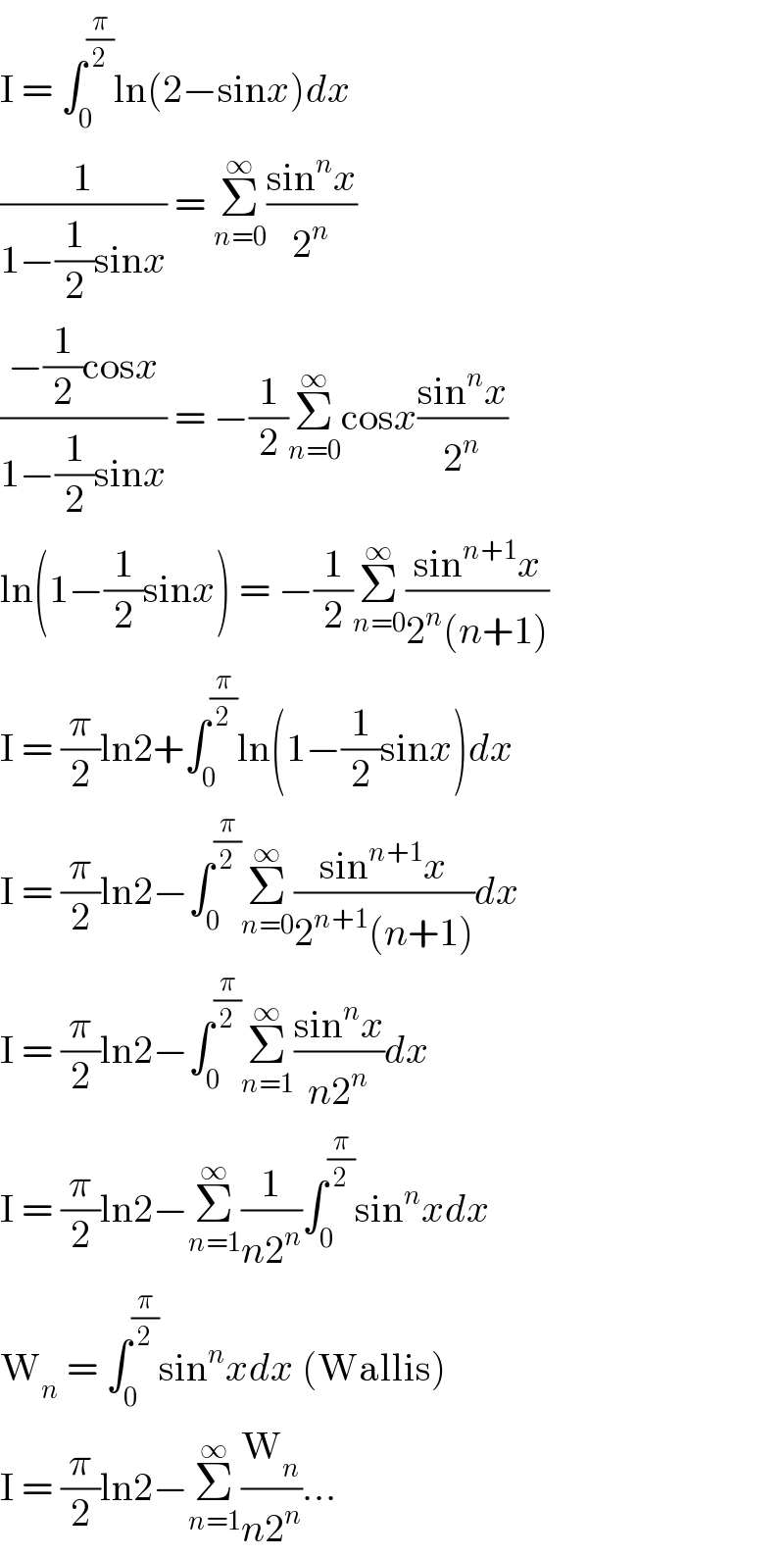
Answered by mathmax by abdo last updated on 15/Sep/20

$$\mathrm{let}\mathrm{I}={\int }_0^{\frac{\pi }{2}}\ln (2-\mathrm{sinx})\mathrm{dx}\Rightarrow \mathrm{I}={\int }_0^{\frac{\pi }{2}}\ln \left(2\right)+\ln (1-\frac{1}{2}\mathrm{sinx})\mathrm{dx}$$$$=\frac{\pi }{2}\ln \left(2\right)+{\int }_0^{\frac{\pi }{2}}\ln (1-\frac{1}{2}\mathrm{sinx})\mathrm{dx}\mathrm{let}\mathrm{f}\left(\mathrm{a}\right)={\int }_0^{\frac{\pi }{2}}\ln (1-\mathrm{asinx})\mathrm{dx}$$$$\mathrm{with}0<\mathrm{a}<1$$$${\mathrm{f}}^{{}^{\prime }}\left(\mathrm{a}\right)={\int }_0^{\frac{\pi }{2}}\frac{-\mathrm{sinx}}{1-\mathrm{asinx}}\mathrm{dx}{=}_{\tan \left(\frac{\mathrm{x}}{2}\right)=\mathrm{t}}-{\int }_0^1\frac{\frac{2\mathrm{t}}{1+{\mathrm{t}}^2}}{1-\mathrm{a}\frac{2\mathrm{t}}{1+{\mathrm{t}}^2}}\times \frac{2\mathrm{dt}}{1+{\mathrm{t}}^2}$$$$=-{\int }_0^1\frac{4\mathrm{t}}{(1+{\mathrm{t}}^2)(1+{\mathrm{t}}^2-2\mathrm{at})}\mathrm{dt}=-4{\int }_0^1\frac{\mathrm{tdt}}{({\mathrm{t}}^2+1)({\mathrm{t}}^2-2\mathrm{at}+1)}$$$$\mathrm{let}\mathrm{decomoose}\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{t}}{({\mathrm{t}}^2-2\mathrm{at}+1)({\mathrm{t}}^2+1)}$$$${\mathrm{t}}^2-2\mathrm{at}+1=0\to {\mathrm{\Delta }}^{{}^{\prime }}={\mathrm{a}}^2-1<0\Rightarrow \mathrm{F}\left(\mathrm{t}\right)=\frac{\alpha \mathrm{t}+\beta }{{\mathrm{t}}^2-2\mathrm{at}+1}+\frac{\mathrm{mt}+\mathrm{n}}{{\mathrm{t}}^2+1}$$$$\Rightarrow (\alpha \mathrm{t}+\beta )({\mathrm{t}}^2+1)+(\mathrm{mt}+\mathrm{n})({\mathrm{t}}^2-2\mathrm{at}+1)=\mathrm{t}\Rightarrow$$$$\alpha {\mathrm{t}}^3+\alpha \mathrm{t}+\beta {\mathrm{t}}^2+\beta +{\mathrm{mt}}^3-{2\mathrm{amt}}^2+\mathrm{mt}+{\mathrm{nt}}^2-2\mathrm{ant}+\mathrm{n}=\mathrm{t}\Rightarrow$$$$(\alpha +\mathrm{m}){\mathrm{t}}^3+(\beta -2\mathrm{am}+\mathrm{n}){\mathrm{t}}^2+(\alpha +\mathrm{m}-2\mathrm{an})\mathrm{t}+\beta +\mathrm{n}=\mathrm{t}\Rightarrow$$$$\{\begin{array}{l}\alpha +\mathrm{m}=0\\ \beta -2\mathrm{am}+\mathrm{n}=0\mathrm{and}\{\begin{array}{l}\alpha +\mathrm{m}-2\mathrm{an}=1\\ \beta +\mathrm{n}=0\Rightarrow \end{array}\end{array}$$$$\{\begin{array}{l}\mathrm{m}=-\alpha \mathrm{and}\{\begin{array}{l}-2\mathrm{an}=1\\ \beta =-\mathrm{n}\Rightarrow \mathrm{n}=-\frac{1}{2\mathrm{a}}\end{array}\\ -2\mathrm{a}\alpha =0\end{array}$$$$\mathrm{and}\alpha =0\Rightarrow \mathrm{m}=0\Rightarrow \mathrm{F}\left(\mathrm{t}\right)=\frac{\frac{1}{2\mathrm{a}}}{{\mathrm{t}}^2-2\mathrm{at}+1}+\frac{-\frac{1}{2\mathrm{a}}}{{\mathrm{t}}^2+1}$$$$=\frac{1}{2\mathrm{a}}\{\frac{1}{{\mathrm{t}}^2-2\mathrm{at}+1}-\frac{1}{{\mathrm{t}}^2+1}\}\Rightarrow$$$${\mathrm{f}}^{{}^{\prime }}\left(\mathrm{a}\right)=-\frac{2}{\mathrm{a}}{\int }_0^1\frac{\mathrm{dt}}{{\mathrm{t}}^2-2\mathrm{at}+1}+\frac{2}{\mathrm{a}}{\int }_0^1\frac{\mathrm{dt}}{{\mathrm{t}}^2+1}$$$$=\frac{2}{\mathrm{a}}\times \frac{\pi }{4}-\frac{2}{\mathrm{a}}{\int }_0^1\frac{\mathrm{dt}}{{\mathrm{t}}^2-2\mathrm{at}+1}=\frac{\pi }{2\mathrm{a}}-\frac{2}{\mathrm{a}}{\int }_0^1\frac{\mathrm{dt}}{{\mathrm{t}}^2-2\mathrm{at}+1}$$$$\mathrm{but}{\int }_0^1\frac{\mathrm{dt}}{{\mathrm{t}}^2-2\mathrm{at}+1}={\int }_0^1\frac{\mathrm{dt}}{{\mathrm{t}}^2-2\mathrm{at}+{\mathrm{a}}^2+1-{\mathrm{a}}^2}={\int }_0^1\frac{\mathrm{dt}}{{(\mathrm{t}-\mathrm{a})}^2+1-{\mathrm{a}}^2}$$$${=}_{\mathrm{t}-\mathrm{a}=\sqrt{1-{\mathrm{a}}^2}\mathrm{u}}{\int }_{\frac{-\mathrm{a}}{\sqrt{1-{\mathrm{a}}^2}}}^{\frac{1-\mathrm{a}}{\sqrt{1-{\mathrm{a}}^2}}}\frac{\sqrt{1-{\mathrm{a}}^2}}{(1-{\mathrm{a}}^2)(1+{\mathrm{u}}^2)}\mathrm{du}$$$$=\frac{1}{\sqrt{1-{\mathrm{a}}^2}}\{\arctan \left(\frac{1-\mathrm{a}}{\sqrt{1-{\mathrm{a}}^2}}\right)+\arctan \left(\frac{\mathrm{a}}{\sqrt{1-{\mathrm{a}}^2}}\right)\}\Rightarrow$$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\pi }{2}\mathrm{lna}-2\int \frac{1}{\mathrm{a}\sqrt{1-{\mathrm{a}}^2}}\arctan \left(\frac{1-\mathrm{a}}{\sqrt{1-{\mathrm{a}}^2}}\right)\mathrm{da}-2\int \frac{1}{\mathrm{a}\sqrt{1-{\mathrm{a}}^2}}\arctan \left(\frac{\mathrm{a}}{\sqrt{1-{\mathrm{a}}^2}}\right)\mathrm{da}$$$$....\mathrm{be}\mathrm{continued}....$$

Commented by mathmax by abdo last updated on 16/Sep/20

$$\mathrm{we}\mathrm{have}\int \frac{1}{\mathrm{a}\sqrt{1-{\mathrm{a}}^2}}\arctan \left(\frac{1-\mathrm{a}}{\sqrt{1-{\mathrm{a}}^2}}\right)\mathrm{da}$$$${=}_{\mathrm{a}=\mathrm{cost}}\int \frac{1}{\mathrm{cost}\mathrm{sint}}\arctan \left(\frac{1-\mathrm{cost}}{\mathrm{sint}}\right)(-\mathrm{sint})\mathrm{dt}$$$$=-\int \frac{1}{\mathrm{cost}}\arctan \left(\frac{{2\sin }^2\left(\frac{\mathrm{t}}{2}\right)}{2\sin \left(\frac{\mathrm{t}}{2}\right)\cos \left(\frac{\mathrm{t}}{2}\right)}\right)\mathrm{dt}$$$$=-\int \frac{1}{\mathrm{cost}}\arctan (\tan \left(\frac{\mathrm{t}}{2}\right)\mathrm{dt}=-\frac{1}{2}\int \frac{\mathrm{t}}{\mathrm{cost}}\mathrm{dt}$$$${=}_{\tan \left(\frac{\mathrm{t}}{2}\right)=\mathrm{z}}-\frac{1}{2}\int \frac{2\arctan \left(\mathrm{z}\right)}{\frac{1-{\mathrm{z}}^2}{1+{\mathrm{z}}^2}}\frac{2\mathrm{dz}}{1+{\mathrm{z}}^2}$$$$=-2\int \frac{\arctan \left(\mathrm{z}\right)}{1-{\mathrm{z}}^2}\mathrm{dz}.....\mathrm{be}\mathrm{continued}...$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com