∫_0 ^(π/2) ln(tan(x)−α)dx=... α∈C


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 138799 by TheSupreme last updated on 18/Apr/21

$\int_{0}^{\frac{π}{2}} \ln (\tan (x) - α) d x = . . .$ $α \in C$
	Answered by mathmax by abdo last updated on 19/Apr/21

	$Φ = \int_{0}^{\frac{π}{2}} \ln (tanx - α) dx \Rightarrow Φ =_{tanx = t} \int_{0}^{\infty} \ln (t - α) \frac{dt}{1 + t^{2}}$ $= \int_{0}^{\infty} \frac{\ln (t - α)}{1 + t^{2}} dt let α = x + iy \Rightarrow t - α = t - x - iy = \sqrt{{(t - x)}^{2} + y^{2}} e^{iarctan (- \frac{y}{t - x})}$ $\Rightarrow Φ = \int_{0}^{\infty} \frac{\ln (\sqrt{{(t - x)}^{2} + y^{2}}) - iarctan (\frac{y}{t - x})}{t^{2} + 1} dt$ $= \frac{1}{2} \int_{0}^{\infty} \frac{\ln ({(t - x)}^{2} + y^{2})}{t^{2} + 1} dt - i \int_{0}^{\infty} \frac{\arctan (\frac{y}{t - x})}{t^{2} + 1} dt we have$ $\int_{0}^{\infty} \frac{\log ({(t - x)}^{2} + y^{2})}{t^{2} + 1} dt = \int_{0}^{\infty} \frac{\log (t^{2} - 2 xt + x^{2} + y^{2})}{t^{2} + 1} dt$ $φ (x) = \int_{0}^{\infty} \frac{\log (t^{2} - 2 xt + x^{2} + y^{2})}{t^{2} + 1} dt \Rightarrow$ $φ^{^{'}} (x) = \int_{0}^{\infty} \frac{- 2 t + 2 x}{(t^{2} - 2 xt + x^{2} + y^{2}) (t^{2} + 1)} dt we must decompose$ $F (t) = \frac{- 2 t + 2 x}{(t^{2} - 2 xt + x^{2} + y^{2}) (t^{2} + 1)} . . . .$ $\int_{0}^{\infty} \frac{\arctan (\frac{y}{t - x})}{t^{2} + 1} dt = \int_{0}^{\infty} \frac{\bar{+} \frac{π}{2} - \arctan (\frac{t - x}{y})}{t^{2} + 1} dt$ $= \bar{+} \frac{π^{2}}{4} - \int_{0}^{\infty} \frac{\arctan (t - x)}{t^{2} + 1} dt + \frac{π}{2} arctany$ $Ψ (x) = \int_{0}^{\infty} \frac{\arctan (t - x)}{t^{2} + 1} dt \Rightarrow Ψ^{^{'}} (x) = \int_{0}^{\infty} \frac{- 1}{(1 + {(t - x)}^{2}) (t^{2} + 1)} dt$ $= - \int_{0}^{\infty} \frac{dt}{(t^{2} - 2 xt + x^{2} + 1) (t^{2} + 1)} rest decomposition . . . be continued . . .$
	Commented by mathmax by abdo last updated on 19/Apr/21

	$sorry \int_{0}^{\infty} \frac{\bar{+} \frac{π}{2} - \arctan (\frac{t - x}{y})}{t^{2} + 1} dt$ $= \bar{+} \frac{π^{2}}{4} - \int_{0}^{\infty} \frac{\arctan (\frac{t}{y} - \frac{x}{y})}{t^{2} + 1} dt so we considere$ $Ψ (x) = \int_{0}^{\infty} \frac{\arctan (\frac{t}{y} - \frac{x}{y})}{t^{2} + 1} dt \Rightarrow$ $Ψ^{^{'}} (y) = \int_{0}^{\infty} \frac{- 1}{y (1 + {(\frac{t}{y} - \frac{x}{y})}^{2}) (t^{2} + 1)} dt = . . . . .$
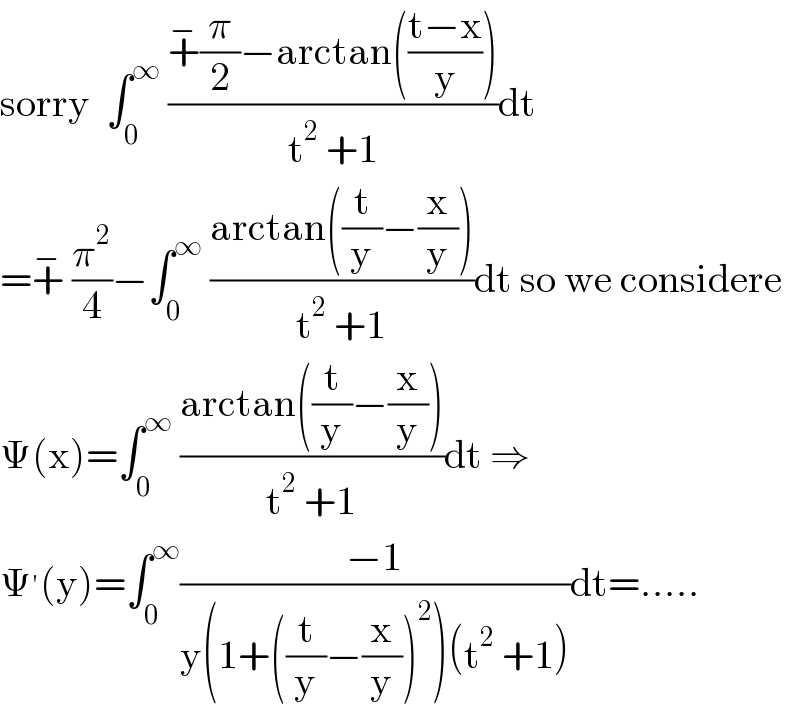
	Commented by mathmax by abdo last updated on 19/Apr/21

	$let try another way Φ = \int_{0}^{\infty} \frac{\log (t - α)}{1 + t^{2}} dt = Ψ (α) \Rightarrow$ $Ψ^{^{'}} (α) = \int_{0}^{\infty} \frac{- 1}{(t - α) (t^{2} + 1)} dt let decompose$ $F (t) = \frac{1}{(t - α) (t^{2} + 1)} \Rightarrow F (t) = \frac{a}{t - α} + \frac{bt + c}{t^{2} + 1}$ $a = \frac{1}{α^{2} + 1}, \lim_{t \to + \infty} tF (t) = 0 = a + b \Rightarrow b = - \frac{1}{α^{2} + 1}$ $F (0) = - \frac{1}{α} = - \frac{a}{α} + c \Rightarrow 1 = a - α c \Rightarrow α c = a - 1 \Rightarrow c = \frac{a - 1}{α}$ $= \frac{\frac{1}{α^{2} + 1} - 1}{α} = - \frac{α^{2}}{α (α^{2} + 1)} = - \frac{α}{α^{2} + 1} \Rightarrow F (t) = \frac{1}{(α^{2} + 1) (t - α)}$ $+ \frac{- \frac{1}{α^{2} + 1} t - \frac{α}{α^{2} + 1}}{t^{2} + 1} \Rightarrow \int_{0}^{\infty} F (t) dt$ $= \frac{1}{α^{2} + 1} \int_{0}^{\infty} \frac{dt}{t - α} - \frac{1}{2 (α^{2} + 1)} \int_{0}^{\infty} \frac{2 t}{t^{2} + 1} dt - \frac{α}{α^{2} + 1} \times \frac{π}{2}$ $= \frac{1}{α^{2} + 1} {[\log (\frac{t - α}{\sqrt{t^{2} + 1}})]}_{0}^{\infty} - \frac{π α}{α^{2} + 1}$ $= \frac{1}{α^{2} + 1} (- \log (- α)) - \frac{π α}{2 (α^{2} + 1)} \Rightarrow Ψ (α) = - \int \frac{\log (- α)}{α^{2} + 1} d α$ $- \frac{π}{4} \log (1 + α^{2}) + C . . . . be continued . . .$
	Answered by phanphuoc last updated on 18/Apr/21

	$u = t g x - > d u / 1 + u^{2} = d x$ $I = \int_{0}^{\infty} l n (u + α) / u^{2} + 1 d u$ $I = 2 π i R e s (f (u), i) = π l n (i + α)$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum