
Question and Answers Forum
Question Number 157096 by amin96 last updated on 19/Oct/21
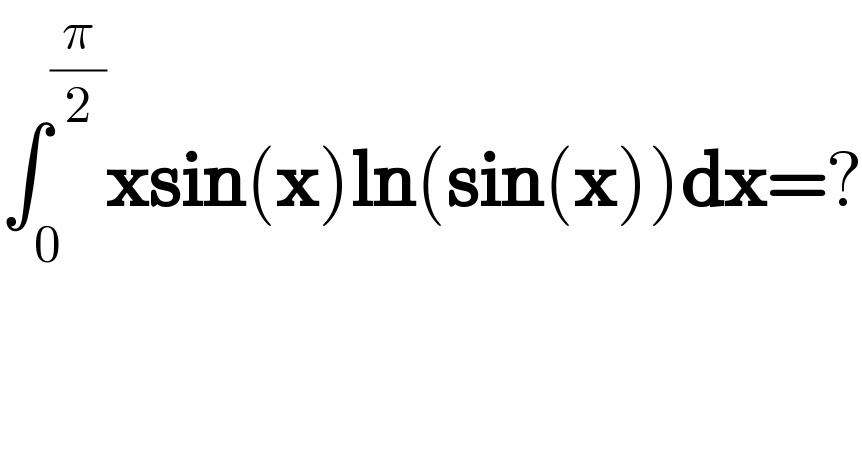
Answered by mindispower last updated on 19/Oct/21
![(−xcos(x)+sin(x))ln(sin(x))]_0 ^(π/2) +∫_0 ^(π/2) ((xcos^2 (x))/(sin(x)))−cosx dx =∫_0 ^(π/2) ((x(1−sin^2 (x)))/(sin(x)))dx−1 =∫_0 ^(π/2) (x/(sin(x)))dx−∫_0 ^(π/2) xsin(x)dx−1 =∫_0 ^(π/2) (x/(sin(x)))dx+[xcos(x)−sin(x)]_0 ^(π/2) −1 =∫_0 ^(π/2) (x/(sin(x)))dx−2,tg((x/2))=u =∫_0 ^1 ((2arctan(u))/u)du=2∫_0 ^1 Σ_(k≥0) (((−1)^k )/(2k+1))u^(2k) −2 =2Σ_(k≥0) (((−1)^k )/((2k+1)^2 ))−2=2(G−1)](Q157112.png)
| ||
Question and Answers Forum | ||
Question Number 157096 by amin96 last updated on 19/Oct/21 | ||
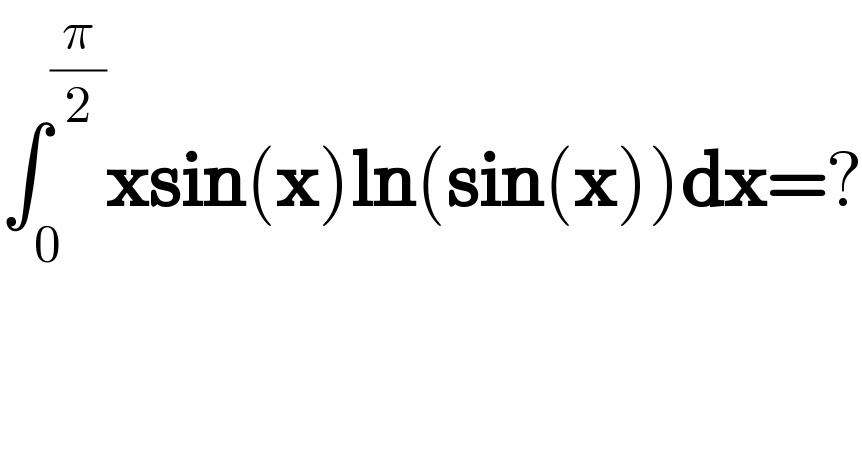 | ||
Answered by mindispower last updated on 19/Oct/21 | ||
![(−xcos(x)+sin(x))ln(sin(x))]_0 ^(π/2) +∫_0 ^(π/2) ((xcos^2 (x))/(sin(x)))−cosx dx =∫_0 ^(π/2) ((x(1−sin^2 (x)))/(sin(x)))dx−1 =∫_0 ^(π/2) (x/(sin(x)))dx−∫_0 ^(π/2) xsin(x)dx−1 =∫_0 ^(π/2) (x/(sin(x)))dx+[xcos(x)−sin(x)]_0 ^(π/2) −1 =∫_0 ^(π/2) (x/(sin(x)))dx−2,tg((x/2))=u =∫_0 ^1 ((2arctan(u))/u)du=2∫_0 ^1 Σ_(k≥0) (((−1)^k )/(2k+1))u^(2k) −2 =2Σ_(k≥0) (((−1)^k )/((2k+1)^2 ))−2=2(G−1)](Q157112.png) | ||
| ||