
Question and Answers Forum
Question Number 182648 by cortano1 last updated on 12/Dec/22
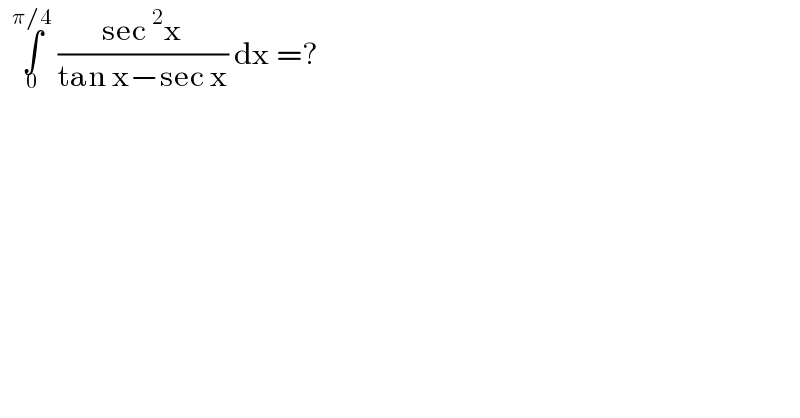
Answered by Acem last updated on 12/Dec/22
![tan x − sec x= t ..... m sec x (sec x− tan x) dx= dt sec x dx= ((−dt)/t) ... i ∗ sec^2 x − tan^2 x= 1 ⇔ (sec x+ tan x) (sec x− tan x)=1 ⇒ sec x + tan x= ((−1)/t) ∗ & sec x − tan x= −t ∗∗^( From m) Sum stars: sec x= −(1/2)((1/t) + t) ...ii i, ii in integ. : I= ∫ ((sec x sec x dx)/(tan x− sec x))= (1/2)∫ ((((1/t) + t))/t^( 2) ) dt I= (1/2) ∫ ((1/t) + (1/t^3 )) dt, from m { ((m=0 : t= −1)),((m= (π/4) : t= 1−(√2) )) :} a= (1/2) ∫_(−1) ^( 1−(√2)) ((1/t) + (1/t^3 )) dt a= (1/2) [ln ∣t∣ − (1/(2 t^2 ))]∣_( −1) ^(1−(√2)) ≈ − 1. 648](Q182665.png)
Answered by FelipeLz last updated on 12/Dec/22
![tan(x) = u → du = sec^2 (x)dx x = 0 → u = 0 x = (π/4) → u = 1 I =∫_0 ^(π/4) ((sec^2 (x))/(tan(x)−sec(x)))dx = ∫_0 ^1 (1/(u−(√(u^2 +1))))du = ∫_0 ^1 (1/(u−(√(u^2 +1))))×((u+(√(u^2 +1)))/(u+(√(u^2 +1))))du = ∫_0 ^1 ((u+(√(u^2 +1)))/(u^2 −u^2 −1))du I = −∫_0 ^1 udu−∫_0 ^1 (√(u^2 +1))du I = −∫_0 ^(π/4) tan(x)sec^2 (x)dx−∫_0 ^(π/4) sec^3 (x)dx ∫tan(x)sec^2 (x)dx = sec^2 (x)−∫tan(x)sec^2 (x)dx 2∫tan(x)sec^2 (x)dx = sec^2 (x) ∫tan(x)sec^2 (x)dx = (1/2)sec^2 (x) ∫sec^3 (x)dx = sec(x)tan(x)−∫sec(x)tan^2 (x)dx ∫sec^3 (x)dx = sec(x)tan(x)−∫sec^3 (x)dx+∫sec(x)dx 2∫sec^3 (x)dx = sec(x)tan(x)+ln∣sec(x)+tan(x)∣ ∫sec^3 (x)dx = (1/2)sec(x)tan(x)+(1/2)ln∣sec(x)+tan(x)∣ I = −(1/2)[sec^2 (x)]_0 ^(π/4) −(1/2)[sec(x)tan(x)+ln∣sec(x)+tan(x)∣]_0 ^(π/4) I = −(1/2)[((√2))^2 −1^2 ]−(1/2)[(√2)×1+ln∣(√2)+1∣−1×0−ln∣1+0∣] I = −(1/2)[1+(√2)+ln(1+(√2))]](Q182670.png)
Answered by MJS_new last updated on 12/Dec/22
![∫((sec^2 x)/(tan x −sec x))dx=∫(dx/(sin 2x −2cos x))= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =2∫((t^2 +1)/((t−1)^3 (t+1)))dt= =(1/2)∫((1/(t−1))−(1/(t+1)))dt+∫((t+1)/((t−1)^3 ))dt= =(1/2)ln ((t−1)/(t+1)) −(t/((t−1)^2 ))= =(1/2)(ln ∣tan x −sec x∣ −(tan x + sec x)tan x)+C ⇒ answer is (1/2)ln (−1+(√2)) −((1+(√2))/2)](Q182692.png)
| ||
Question and Answers Forum | ||
Question Number 182648 by cortano1 last updated on 12/Dec/22 | ||
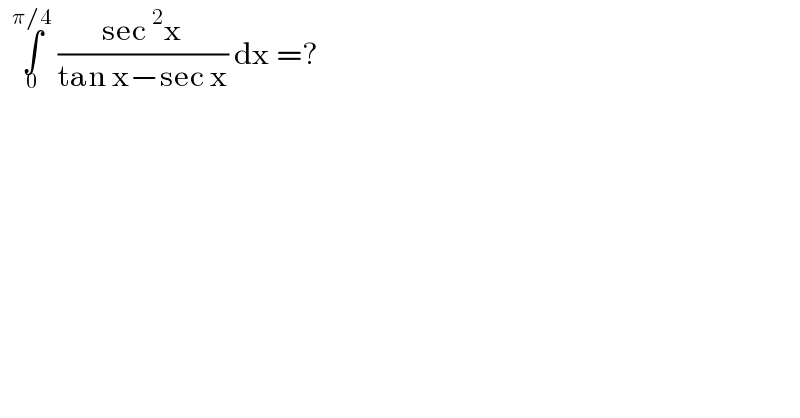 | ||
Answered by Acem last updated on 12/Dec/22 | ||
![tan x − sec x= t ..... m sec x (sec x− tan x) dx= dt sec x dx= ((−dt)/t) ... i ∗ sec^2 x − tan^2 x= 1 ⇔ (sec x+ tan x) (sec x− tan x)=1 ⇒ sec x + tan x= ((−1)/t) ∗ & sec x − tan x= −t ∗∗^( From m) Sum stars: sec x= −(1/2)((1/t) + t) ...ii i, ii in integ. : I= ∫ ((sec x sec x dx)/(tan x− sec x))= (1/2)∫ ((((1/t) + t))/t^( 2) ) dt I= (1/2) ∫ ((1/t) + (1/t^3 )) dt, from m { ((m=0 : t= −1)),((m= (π/4) : t= 1−(√2) )) :} a= (1/2) ∫_(−1) ^( 1−(√2)) ((1/t) + (1/t^3 )) dt a= (1/2) [ln ∣t∣ − (1/(2 t^2 ))]∣_( −1) ^(1−(√2)) ≈ − 1. 648](Q182665.png) | ||
| ||
Answered by FelipeLz last updated on 12/Dec/22 | ||
![tan(x) = u → du = sec^2 (x)dx x = 0 → u = 0 x = (π/4) → u = 1 I =∫_0 ^(π/4) ((sec^2 (x))/(tan(x)−sec(x)))dx = ∫_0 ^1 (1/(u−(√(u^2 +1))))du = ∫_0 ^1 (1/(u−(√(u^2 +1))))×((u+(√(u^2 +1)))/(u+(√(u^2 +1))))du = ∫_0 ^1 ((u+(√(u^2 +1)))/(u^2 −u^2 −1))du I = −∫_0 ^1 udu−∫_0 ^1 (√(u^2 +1))du I = −∫_0 ^(π/4) tan(x)sec^2 (x)dx−∫_0 ^(π/4) sec^3 (x)dx ∫tan(x)sec^2 (x)dx = sec^2 (x)−∫tan(x)sec^2 (x)dx 2∫tan(x)sec^2 (x)dx = sec^2 (x) ∫tan(x)sec^2 (x)dx = (1/2)sec^2 (x) ∫sec^3 (x)dx = sec(x)tan(x)−∫sec(x)tan^2 (x)dx ∫sec^3 (x)dx = sec(x)tan(x)−∫sec^3 (x)dx+∫sec(x)dx 2∫sec^3 (x)dx = sec(x)tan(x)+ln∣sec(x)+tan(x)∣ ∫sec^3 (x)dx = (1/2)sec(x)tan(x)+(1/2)ln∣sec(x)+tan(x)∣ I = −(1/2)[sec^2 (x)]_0 ^(π/4) −(1/2)[sec(x)tan(x)+ln∣sec(x)+tan(x)∣]_0 ^(π/4) I = −(1/2)[((√2))^2 −1^2 ]−(1/2)[(√2)×1+ln∣(√2)+1∣−1×0−ln∣1+0∣] I = −(1/2)[1+(√2)+ln(1+(√2))]](Q182670.png) | ||
| ||
Answered by MJS_new last updated on 12/Dec/22 | ||
![∫((sec^2 x)/(tan x −sec x))dx=∫(dx/(sin 2x −2cos x))= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =2∫((t^2 +1)/((t−1)^3 (t+1)))dt= =(1/2)∫((1/(t−1))−(1/(t+1)))dt+∫((t+1)/((t−1)^3 ))dt= =(1/2)ln ((t−1)/(t+1)) −(t/((t−1)^2 ))= =(1/2)(ln ∣tan x −sec x∣ −(tan x + sec x)tan x)+C ⇒ answer is (1/2)ln (−1+(√2)) −((1+(√2))/2)](Q182692.png) | ||
| ||