
Question and Answers Forum
Question Number 65100 by arcana last updated on 25/Jul/19
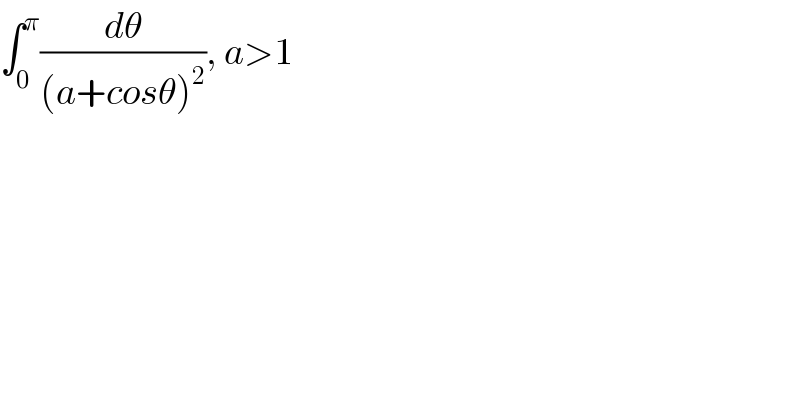
Commented by ~ À ® @ 237 ~ last updated on 25/Jul/19
![let g(a)=∫_0 ^π (dθ/(a+cosθ )) then ∫_0 ^π (dθ/((a+cosθ)^2 ))=−(dg/(da )) so let find g(a) g(a)=∫_0 ^π (dθ/((a−1)+2cos^2 ((θ/2))))=∫_0 ^(π/2) ((2dx)/((a−1)[cos^2 x+sin^2 x]+2cos^2 x))=2∫_0 ^(π/2) (dx/((a+1)cos^2 x +(a−1)sin^2 x)) then ((g(a))/2)= ∫_0 ^(π/2) (((1/(cos^2 x)) dx)/((a+1)+(a−1)tan^2 x)) we have a>1⇒(a+1)+(a−1)tan^2 x=(a+1)[1+((√((a−1)/(a+1)))tanx)^2 ] ((g(a))/2)=(1/(√(a^2 −1)))∫_0 ^(π/2) (((√((a−1)/(a+1))) (1+tan^2 x) dx)/(1+((√(((a−1)/(a+1)) )) tanx)^2 )) So we get g(a)=(2/(√(a^2 −1))) [arctan((√(((a−1)/(a+1)) )) tanx)]_0 ^(π/2) = (π/(√(a^2 −1))) then (dg/da)=π.((((−2a)/(2(√(a^2 −1))))/(a^2 −1)))= ((−πa)/((a^2 −1)^(3/2) )) that leads us to ∫_(0 ) ^π (dθ/((a+cosθ)^2 )) = ((πa)/((a^2 −1)^(3/2) ))](Q65104.png)
Commented by turbo msup by abdo last updated on 25/Jul/19
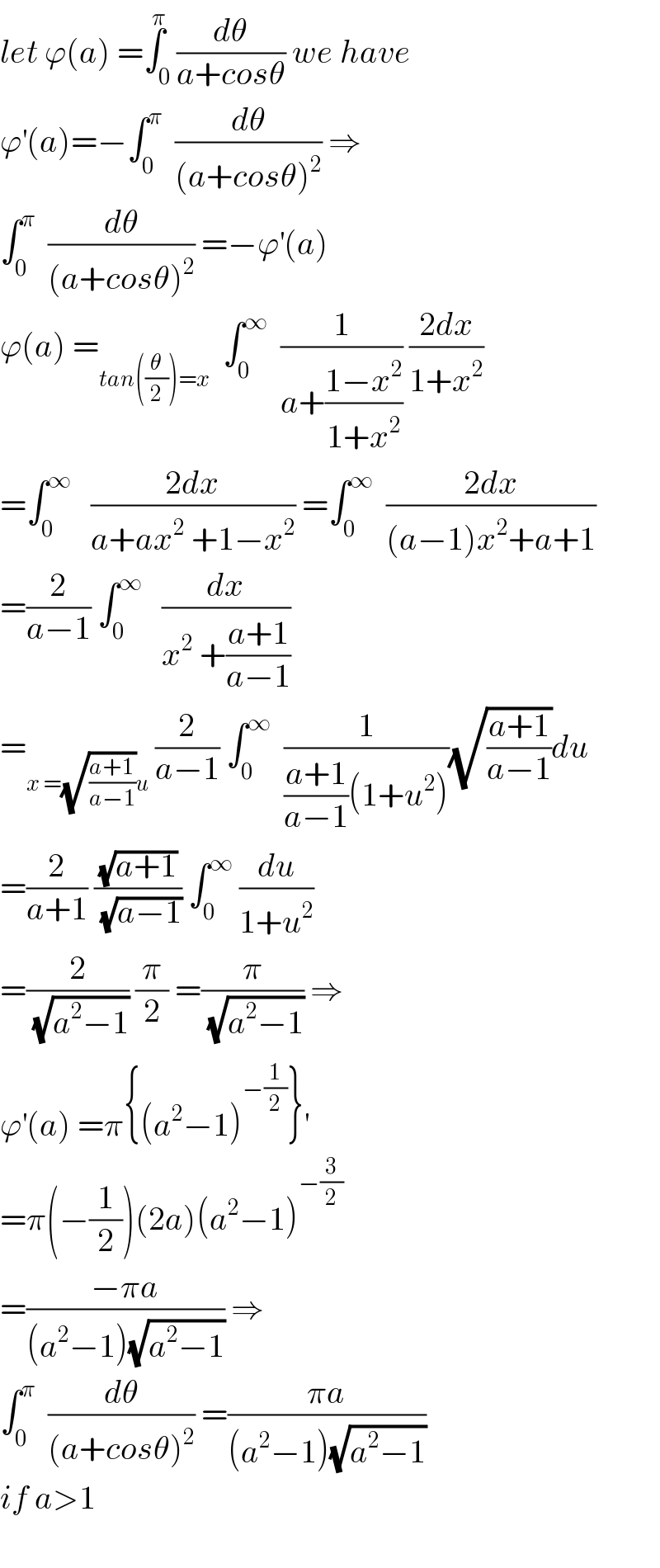
Commented by arcana last updated on 25/Jul/19

Commented by arcana last updated on 25/Jul/19

Commented by turbo msup by abdo last updated on 25/Jul/19

Commented by arcana last updated on 25/Jul/19
Commented by mathmax by abdo last updated on 25/Jul/19
Commented by arcana last updated on 26/Jul/19

