∫_0 ^( π) ((xtan x)/(sec x+tan x))dx = (is it (π^2 /2)−π)?


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 55930 by ajfour last updated on 06/Mar/19

$\int_{0}^{π} \frac{x \tan x}{\sec x + \tan x} d x = (i s i t \frac{π^{2}}{2} - π) ?$
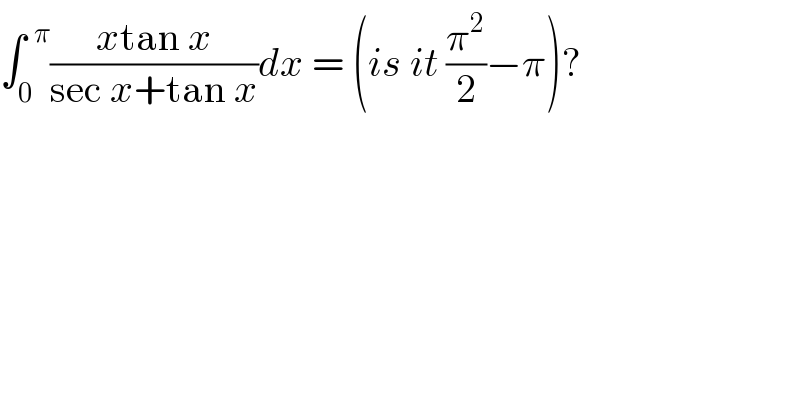
	Answered by tanmay.chaudhury50@gmail.com last updated on 06/Mar/19

	$\int_{0}^{π} \frac{x s i n x}{1 + s i n x} d x$ $I = \int_{0}^{π} \frac{(π - x) s i n (π - x)}{1 + s i n (π - x)} d x$ $= \int_{0}^{π} \frac{(π - x) s i n x}{1 + s i n x} d x$ $2 I = \int_{0}^{π} \frac{π s i n x - x s i n x + x s i n x}{1 + s i n x} d x$ $2 I = π \int_{0}^{π} \frac{s i n x}{1 + s i n x} d x$ $= π \int_{0}^{π} (1 - \frac{1}{1 + s i n x}) d x$ $\frac{2 I}{π} = \int_{0}^{π} d x - \int_{0}^{π} \frac{1 - s i n x}{{c o s}^{2} x} d x$ $\frac{2 I}{π} = \int_{0}^{π} d x - \int_{0}^{π} {s e c}^{2} x d x + \int_{0}^{π} s e c x t a n x d x$ $\frac{2 I}{π} =∣ x - t a n x + s e c x ∣_{0}^{π}$ $\frac{2 I}{π} = (π - 0 - 1) - (0 - 0 + 1)$ $\frac{2 I}{π} = π - 1 - 1$ $2 I = π^{2} - 2 π$ $I = \frac{π^{2}}{2} - π$
	Commented by ajfour last updated on 06/Mar/19

	$T h a n k s S i r, g r e a t!$
	Commented by tanmay.chaudhury50@gmail.com last updated on 06/Mar/19

	$t h a n k y o u s i r . . .$
	Commented by maxmathsup by imad last updated on 09/Mar/19
	$I =∫_0 ^π ((x(1+sinx−1))/(1+sinx))dx =∫_0 ^π xdx −∫_0 ^π (x/(1+sinx)) dx but ∫_0 ^π xdx =[(x^2 /2)]_0 ^π =(π^2 /2) and ∫_0 ^π (x/(1+sinx)) dx =_(tan((x/2))=t) ∫_0 ^∞ ((2arctan(t))/(1+((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) =4 ∫_0 ^∞ ((arctan(t))/(1+t^2 +2t)) dt =4 ∫_0 ^∞ ((arctan(t))/((t+1)^2 )) dt ( and by parts) =4{ [−((arctan(t))/(t+1))]_0 ^∞ +∫_0 ^∞ (1/((t+1)(t^2 +1)))dt} =4 ∫_0 ^∞ (dt/((t+1)(t^2 +1))) dt let decompose F(t) =(1/((t+1)(t^2 +1))) ⇒ F(t) =(a/(t+1)) +((bt +c)/(t^2 +1)) a =lim_(t→−1) (t+1)F(t) = (1/2) lim_(t→+∞) tF(t) = 0 =a+b ⇒b =−a =−(1/2) ⇒F(t)=(1/(2(t+1))) +((−(t/2)+c)/(t^2 +1)) F(0) =1 =(1/2) +c ⇒c=(1/2) ⇒F(t)=(1/(2(t+1))) −(1/2) ((t−1)/(t^2 +1)) ⇒ ∫_0 ^∞ F(t)dt =(1/2)[ln∣t+1∣−(1/2)ln(t^2 +1)]_0 ^(+∞) +(1/2)[arctan(t)]_0 ^(+∞) =(1/2)[ln∣((t+1)/(√(t^2 +1)))∣]_0 ^∞ +(π/4) =(π/4) ⇒ I =(π^2 /2) −4((π/4)) =(π^2 /2)−π .$
	$I = \int_{0}^{π} \frac{x (1 + s i n x - 1)}{1 + s i n x} d x = \int_{0}^{π} x d x - \int_{0}^{π} \frac{x}{1 + s i n x} d x b u t$ $\int_{0}^{π} x d x = {[\frac{x^{2}}{2}]}_{0}^{π} = \frac{π^{2}}{2} a n d \int_{0}^{π} \frac{x}{1 + s i n x} d x =_{t a n (\frac{x}{2}) = t} \int_{0}^{\infty} \frac{2 a r c t a n (t)}{1 + \frac{2 t}{1 + t^{2}}} \frac{2 d t}{1 + t^{2}}$ $= 4 \int_{0}^{\infty} \frac{a r c t a n (t)}{1 + t^{2} + 2 t} d t = 4 \int_{0}^{\infty} \frac{a r c t a n (t)}{{(t + 1)}^{2}} d t (a n d b y p a r t s)$ $= 4 {{[- \frac{a r c t a n (t)}{t + 1}]}_{0}^{\infty} + \int_{0}^{\infty} \frac{1}{(t + 1) (t^{2} + 1)} d t}$ $= 4 \int_{0}^{\infty} \frac{d t}{(t + 1) (t^{2} + 1)} d t l e t d e c o m p o s e F (t) = \frac{1}{(t + 1) (t^{2} + 1)} \Rightarrow$ $F (t) = \frac{a}{t + 1} + \frac{b t + c}{t^{2} + 1}$ $a = {l i m}_{t \to - 1} (t + 1) F (t) = \frac{1}{2}$ ${l i m}_{t \to + \infty} t F (t) = 0 = a + b \Rightarrow b = - a = - \frac{1}{2} \Rightarrow F (t) = \frac{1}{2 (t + 1)} + \frac{- \frac{t}{2} + c}{t^{2} + 1}$ $F (0) = 1 = \frac{1}{2} + c \Rightarrow c = \frac{1}{2} \Rightarrow F (t) = \frac{1}{2 (t + 1)} - \frac{1}{2} \frac{t - 1}{t^{2} + 1} \Rightarrow$ $\int_{0}^{\infty} F (t) d t = \frac{1}{2} {[l n ∣ t + 1 ∣ - \frac{1}{2} l n (t^{2} + 1)]}_{0}^{+ \infty} + \frac{1}{2} {[a r c t a n (t)]}_{0}^{+ \infty}$ $= \frac{1}{2} {[l n ∣ \frac{t + 1}{\sqrt{t^{2} + 1}} ∣]}_{0}^{\infty} + \frac{π}{4} = \frac{π}{4} \Rightarrow$ $I = \frac{π^{2}}{2} - 4 (\frac{π}{4}) = \frac{π^{2}}{2} - π .$
	Answered by MJS last updated on 06/Mar/19

	$\int \frac{x \tan x}{\sec x + \tan x} d x = \int \frac{x \sin x}{1 + \sin x} d x = \int x d x - \int \frac{x}{1 + \sin x} d x =$ $= \frac{x^{2}}{2} - \int \frac{x}{1 + \sin x} d x =$ $\int \frac{x}{1 + \sin x} d x =$ $[\int u^{'} v = u v - \int {u v}^{'}; u^{'} = \frac{1}{1 + \sin x}; v = x$ $u = - \frac{\cos x}{1 + \sin x}; v^{'} = 1]$ $= - \frac{x \cos x}{1 + \sin x} + \int \frac{\cos x}{1 + \sin x} d x =$ $= - \frac{x \cos x}{1 + \sin x} + \ln (1 + \sin x)$ $= \frac{x^{2}}{2} + \frac{x \cos x}{1 + \sin x} - \ln (1 + \sin x) + C$ $\Rightarrow your value is true$
	Commented by ajfour last updated on 06/Mar/19

	$T h a n k s M J S S i r!$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum