
Question and Answers Forum
Question Number 101793 by Dwaipayan Shikari last updated on 04/Jul/20
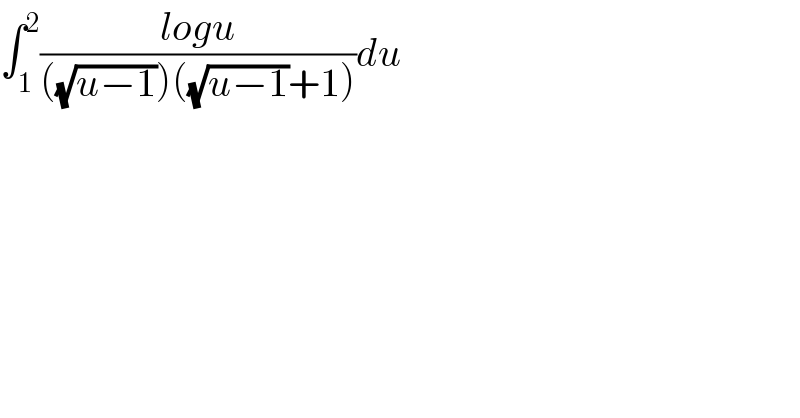
Answered by mathmax by abdo last updated on 05/Jul/20
![I =∫_1 ^(2 ) ((ln(u))/((√(u−1))((√(u−1))+1)))du changement (√(u−1))=x give u−1 =x^2 ⇒ I =∫_0 ^1 ((ln(1+x^2 ))/(x(x+1))) (2x)dx =2 ∫_0 ^1 ((ln(1+x^2 ))/(1+x)) dx =2 ∫_0 ^1 ln(1+x^2 )Σ_(n=0) ^∞ (−1)^n x^n =2 Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^n ln(1+x^2 )dx =2 Σ_(n=0) ^∞ (−1)^n A_n with A_n =∫_0 ^1 x^n ln(1+x^2 )dx by parts we get A_n =[(x^(n+1) /(n+1))ln(1+x^2 )]_0 ^1 −∫_0 ^1 (x^(n+1) /(n+1))×((2x)/(1+x^2 ))dx =((ln(2))/(n+1))−(2/(n+1))∫_0 ^1 (x^(n+2) /(1+x^2 ))dx ∫_0 ^1 (x^(n+2) /(1+x^2 ))dx =∫_0 ^1 (((x^2 +1−1)x^n )/(1+x^2 ))dx =∫_0 ^1 x^n dx−∫_0 ^1 (x^n /(x^2 +1))dx =(1/(n+1))−∫_0 ^(1 ) (x^n /(x^2 +1))dx we have ∫_0 ^1 (x^n /(x^2 +1))dx =∫_0 ^1 x^n (Σ_(k=0) ^∞ (−1)^k x^(2k) ) =Σ_(k=0) ^∞ (−1)^k ∫_0 ^1 x^(n+2k) dx =Σ_(k=0) ^∞ (−1)^k ×(1/(n+2k+1)) ⇒ A_n =((ln2)/(n+1))−(2/(n+1)){(1/(n+1))−Σ_(k=0) ^∞ (((−1)^k )/(2k+n+1))} =((ln2)/(n+1))−(2/((n+1)^2 )) −(2/(n+1)) Σ_(k=0) ^∞ (((−1)^k )/(2k+n+1)) ⇒ I =2ln2 Σ_(n=0) ^∞ (((−1)^n )/(n+1))−4 Σ_(n=0) ^∞ (((−1)^n )/((n+1)^2 )) −4 Σ_(n=0) ^∞ (((−1)^n )/(n+1))(Σ_(k=0) ^∞ (((−1)^k )/(2k+n+1))) Σ_(n=0) ^∞ (((−1)^n )/(n+1)) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) =ln(2) Σ_(n=0) ^∞ (((−1)^n )/((n+1)^2 )) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) =−Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =−{2^(1−2) −1)ξ(2) =−(−(1/2))×(π^2 /6) =(π^2 /(12)) Σ_(n=0) ^∞ (((−1)^n )/(n+1))Σ_(k=0) ^∞ (((−1)^k )/(2k+n+1)) =Σ_(n=0) ^∞ Σ_(k=0) ^∞ (((−1)^(n+k) )/((n+1)(2k+n+1))) ...be continued...](Q101829.png)
Commented by 1549442205 last updated on 06/Jul/20
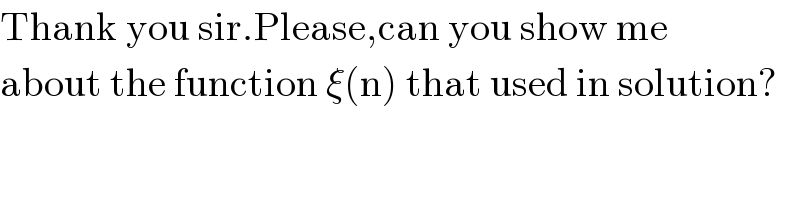
| ||
Question and Answers Forum | ||
Question Number 101793 by Dwaipayan Shikari last updated on 04/Jul/20 | ||
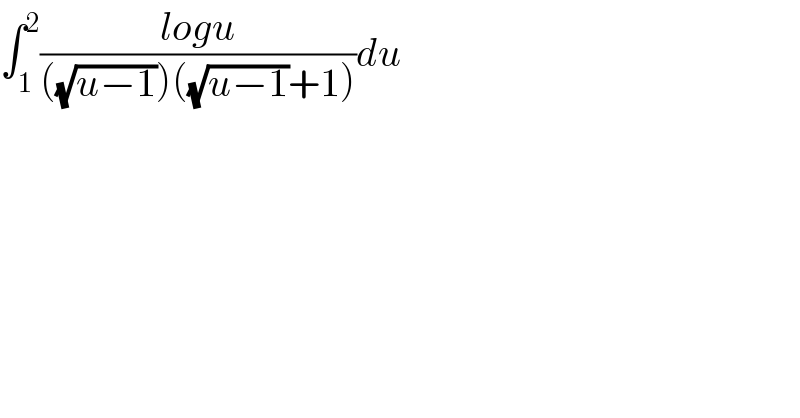 | ||
Answered by mathmax by abdo last updated on 05/Jul/20 | ||
![I =∫_1 ^(2 ) ((ln(u))/((√(u−1))((√(u−1))+1)))du changement (√(u−1))=x give u−1 =x^2 ⇒ I =∫_0 ^1 ((ln(1+x^2 ))/(x(x+1))) (2x)dx =2 ∫_0 ^1 ((ln(1+x^2 ))/(1+x)) dx =2 ∫_0 ^1 ln(1+x^2 )Σ_(n=0) ^∞ (−1)^n x^n =2 Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^n ln(1+x^2 )dx =2 Σ_(n=0) ^∞ (−1)^n A_n with A_n =∫_0 ^1 x^n ln(1+x^2 )dx by parts we get A_n =[(x^(n+1) /(n+1))ln(1+x^2 )]_0 ^1 −∫_0 ^1 (x^(n+1) /(n+1))×((2x)/(1+x^2 ))dx =((ln(2))/(n+1))−(2/(n+1))∫_0 ^1 (x^(n+2) /(1+x^2 ))dx ∫_0 ^1 (x^(n+2) /(1+x^2 ))dx =∫_0 ^1 (((x^2 +1−1)x^n )/(1+x^2 ))dx =∫_0 ^1 x^n dx−∫_0 ^1 (x^n /(x^2 +1))dx =(1/(n+1))−∫_0 ^(1 ) (x^n /(x^2 +1))dx we have ∫_0 ^1 (x^n /(x^2 +1))dx =∫_0 ^1 x^n (Σ_(k=0) ^∞ (−1)^k x^(2k) ) =Σ_(k=0) ^∞ (−1)^k ∫_0 ^1 x^(n+2k) dx =Σ_(k=0) ^∞ (−1)^k ×(1/(n+2k+1)) ⇒ A_n =((ln2)/(n+1))−(2/(n+1)){(1/(n+1))−Σ_(k=0) ^∞ (((−1)^k )/(2k+n+1))} =((ln2)/(n+1))−(2/((n+1)^2 )) −(2/(n+1)) Σ_(k=0) ^∞ (((−1)^k )/(2k+n+1)) ⇒ I =2ln2 Σ_(n=0) ^∞ (((−1)^n )/(n+1))−4 Σ_(n=0) ^∞ (((−1)^n )/((n+1)^2 )) −4 Σ_(n=0) ^∞ (((−1)^n )/(n+1))(Σ_(k=0) ^∞ (((−1)^k )/(2k+n+1))) Σ_(n=0) ^∞ (((−1)^n )/(n+1)) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) =ln(2) Σ_(n=0) ^∞ (((−1)^n )/((n+1)^2 )) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) =−Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =−{2^(1−2) −1)ξ(2) =−(−(1/2))×(π^2 /6) =(π^2 /(12)) Σ_(n=0) ^∞ (((−1)^n )/(n+1))Σ_(k=0) ^∞ (((−1)^k )/(2k+n+1)) =Σ_(n=0) ^∞ Σ_(k=0) ^∞ (((−1)^(n+k) )/((n+1)(2k+n+1))) ...be continued...](Q101829.png) | ||
| ||
Commented by 1549442205 last updated on 06/Jul/20 | ||
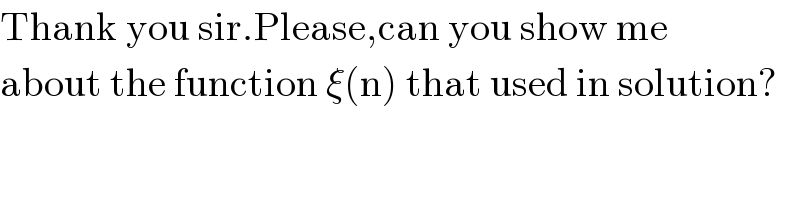 | ||