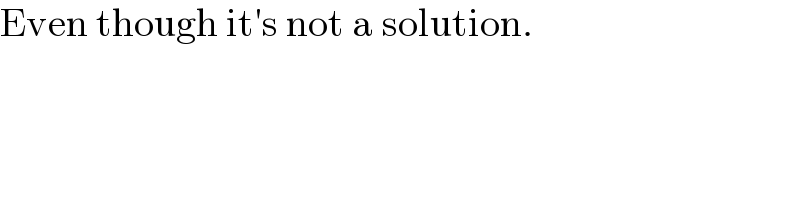Question and Answers Forum
Question Number 214658 by ChantalYah last updated on 15/Dec/24

Answered by a.lgnaoui last updated on 16/Dec/24
![2)∫_2 ^4 ((6x+1)/((2x−3)(3x−2)))dx= ((6x+1)/((2x−3)(3x−2)))=(a/(2x−3))+(b/((3x−2))) =(((3a+2b)x−(2a+3b))/((2x−3)(3x−2))) { ((3a+2b=6 ×2)),((2a+3b=−1 ×−3)) :} −5b=15 ⇒ a=4 b=−3 ∫_2 ^4 ((6x+1)/((2x−3)(3x+2)))= ∫(4/(2x−3))dx−∫(3/(3x−2))dx •2[ln(2x−3)]_2 ^4 −[ln(3x−2) −(ln(3x−2)]_2 ^4 = 2[ln(5)−(ln10)+ln4=ln5+ln2=ln10 •3)((sin 𝛉+sin 2𝛉)/(1+cos 𝛉+cos 2𝛉))=((sin𝛉(1+2cos 𝛉) )/(cos 𝛉(1+2cos 𝛉))) tan 𝛉 •4)if z=cos 𝛉+isin 𝛉 z+(1/z)=cos 𝛉+isin 𝛉+((cos 𝛉−isin 𝛉)/1) =2cos 𝛉 ⇒ z^n +(1/z^n )=2cos n𝛉 32cos 6𝛉=2^5 cos 6𝛉=2^4 ×(2cos 6𝛉) 2^4 [(cos 6𝛉+isin 6𝛉)+(1/(cos 6𝛉+isin 6𝛉)) =2^5 (2cos^2 3𝛉−1) cos 3𝛉=4cos^3 𝛉−3cos 𝛉 cos 6𝛉=2cos^2 3𝛉−1 =2cos^2 𝛉(4cos^2 𝛉−3)^2 −1 =2(16cos^6 𝛉−24cos^4 𝛉+9cos^2 𝛉)−1 soit 32cos^6 𝛉=cos 6𝛉+48cos^4 𝛉−18cos^2 𝛉+1 cos 4𝛉=2(2cos^2 𝛉−1)^2 −1 =2(4cos^4 𝛉+1−4cos^2 𝛉)−1 =8cos^4 𝛉−8cos^2 𝛉+1 ⇒ 48cos^4 𝛉−18cos^2 𝛉 =6cos 4𝛉+30cos^2 𝛉 32cos^6 𝛉=cos 6𝛉+6cos 4𝛉+30cos^2 𝛉 =cos 6𝛉+6cos 4𝛉+15(cos 2𝛉)+10 i](Q214670.png)
Answered by MathematicalUser2357 last updated on 16/Dec/24

Commented by MathematicalUser2357 last updated on 17/Dec/24