
Question and Answers Forum
Question Number 126105 by Mathgreat last updated on 17/Dec/20
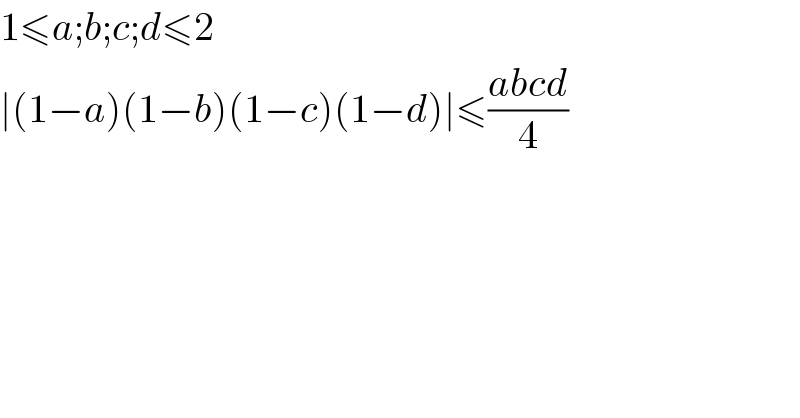
Commented by Mathgreat last updated on 17/Dec/20

Answered by talminator2856791 last updated on 17/Dec/20
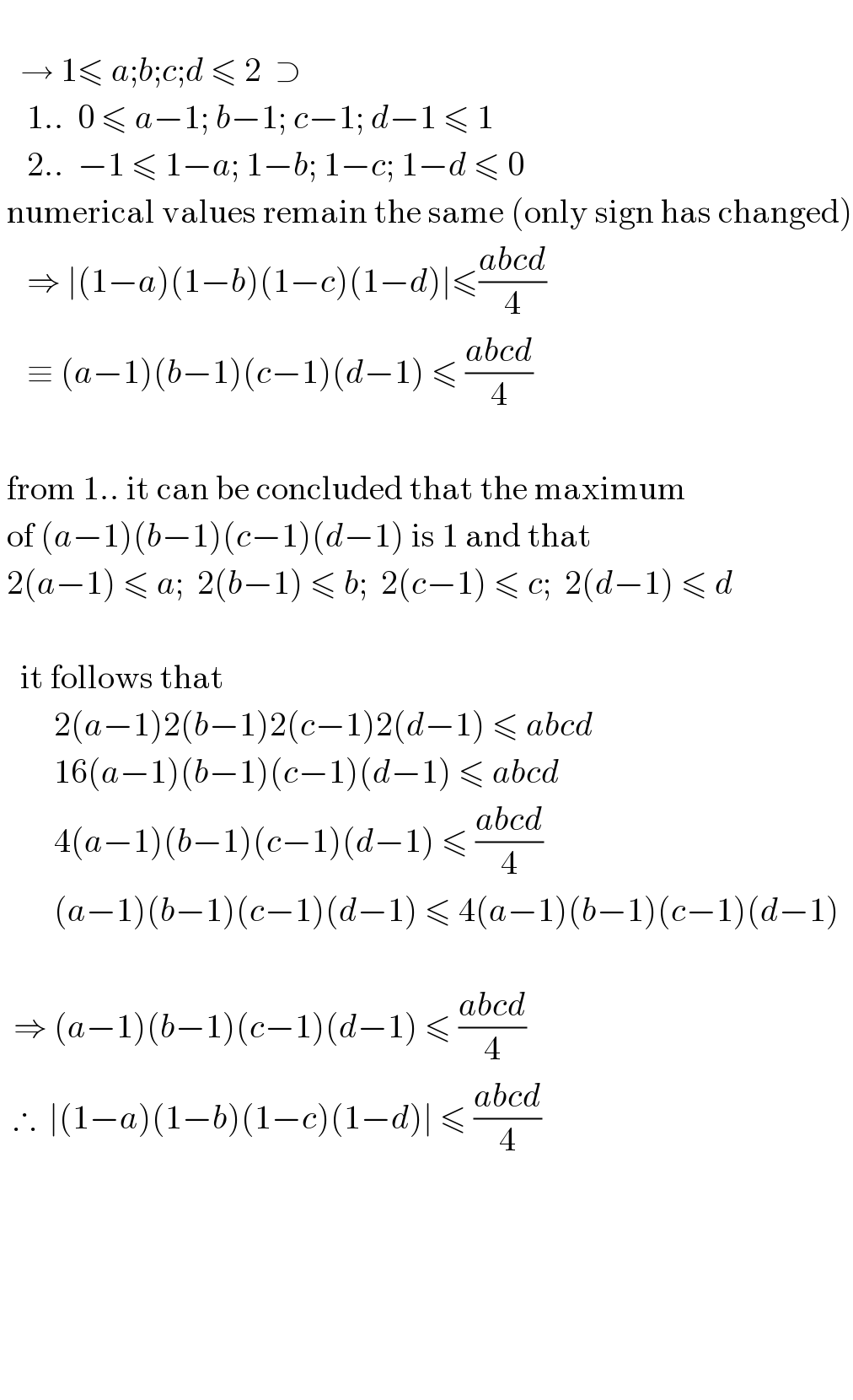
| ||
Question and Answers Forum | ||
Question Number 126105 by Mathgreat last updated on 17/Dec/20 | ||
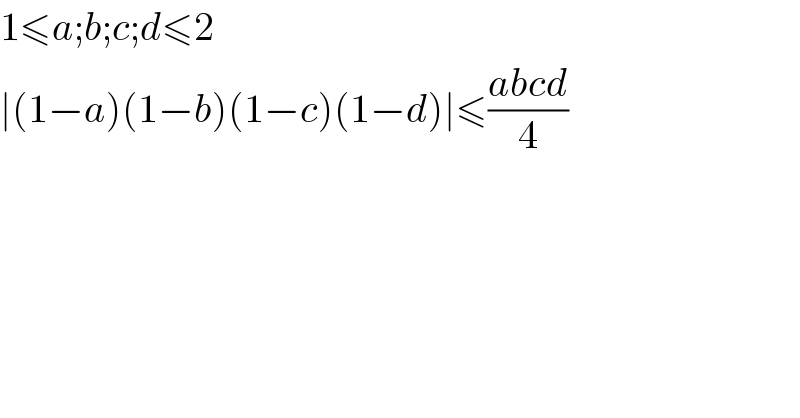 | ||
Commented by Mathgreat last updated on 17/Dec/20 | ||
 | ||
Answered by talminator2856791 last updated on 17/Dec/20 | ||
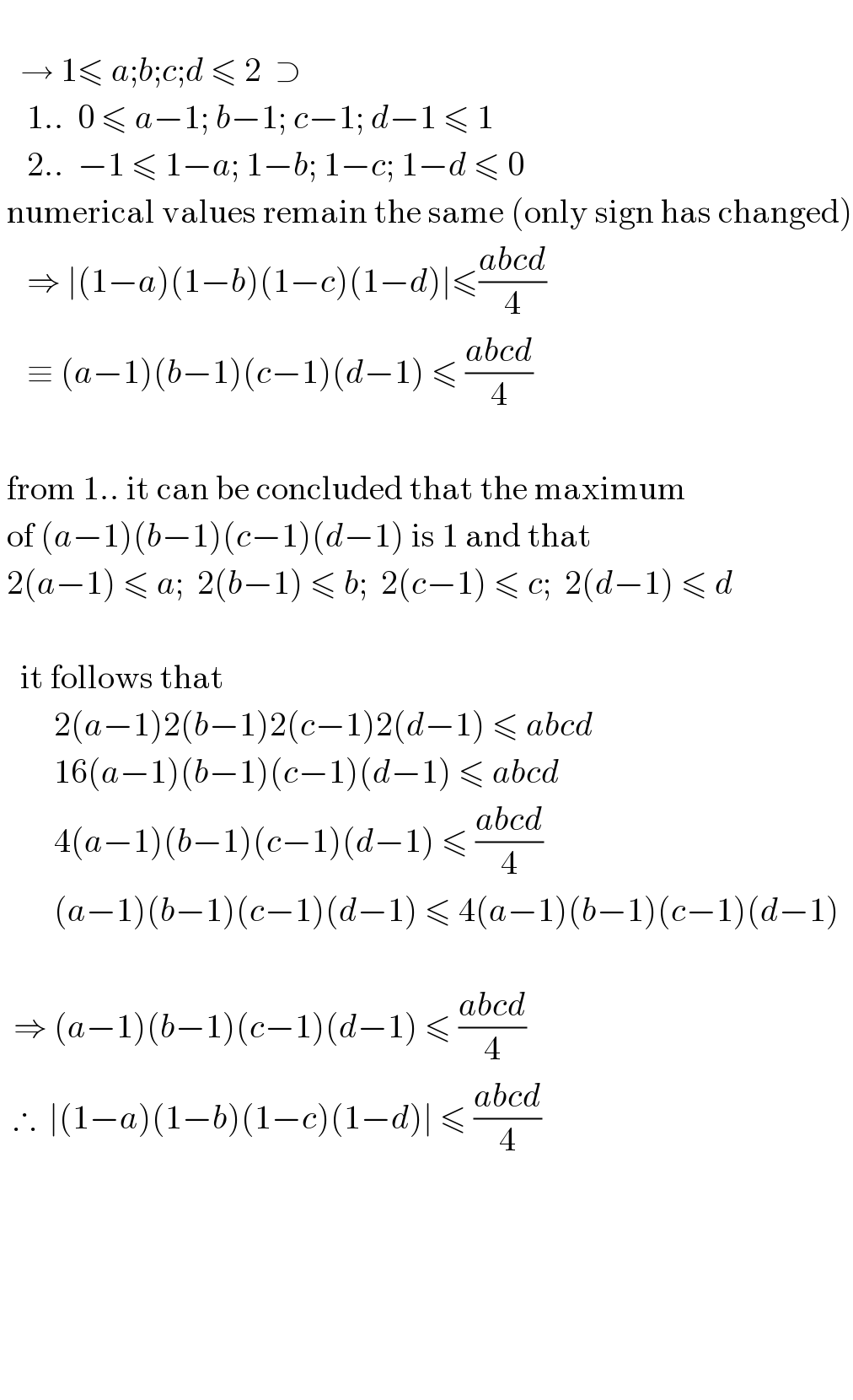 | ||
| ||