
Question and Answers Forum
Question Number 53271 by Abdo msup. last updated on 19/Jan/19
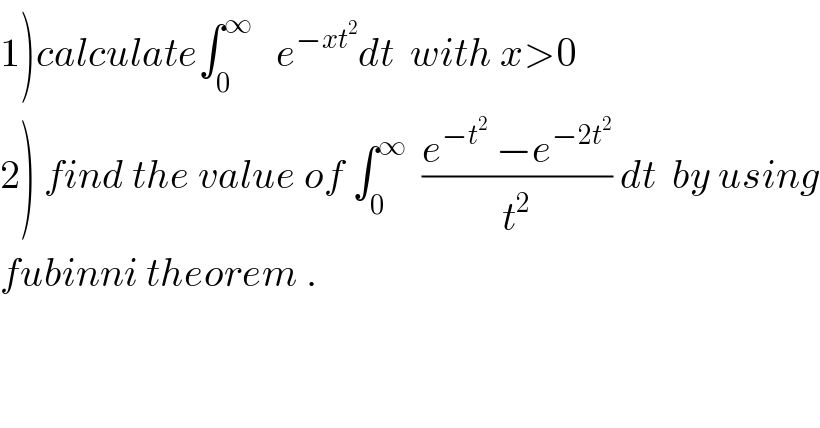
Commented by maxmathsup by imad last updated on 22/Jan/19
![1) we have ∫_0 ^∞ e^(−xt^2 ) dt =_(t(√x)=u) ∫_0 ^∞ e^(−u^2 ) (du/(√x)) =(1/(√x)) ∫_0 ^∞ e^(−u^2 ) du =(1/(√x)) ((√π)/2) =((√π)/(2(√x))) 2) we have ∫_1 ^2 ((√π)/(2(√x))) dx =(√π)[(√x)]_1 ^2 =(√π)((√2)−1) but ∫_1 ^2 ((√π)/(2(√x))) dx =∫_1 ^2 (∫_0 ^∞ e^(−xt^2 ) dt)dx =∫_0 ^∞ ( ∫_1 ^2 e^(−xt^2 ) dx)dt (by fubini) =∫_0 ^∞ ( [−(1/t^2 ) e^(−xt^2 ) ]_(x=1) ^(x=2) )dt =∫_0 ^∞ ((e^(−t^2 ) −e^(−2t^2 ) )/t^2 ) dt ⇒ ∫_0 ^∞ ((e^(−t^2 ) −e^(−2t^2 ) )/t^2 ) dt =(√π)((√2)−1)](Q53457.png)
Commented by maxmathsup by imad last updated on 22/Jan/19

| ||
Question and Answers Forum | ||
Question Number 53271 by Abdo msup. last updated on 19/Jan/19 | ||
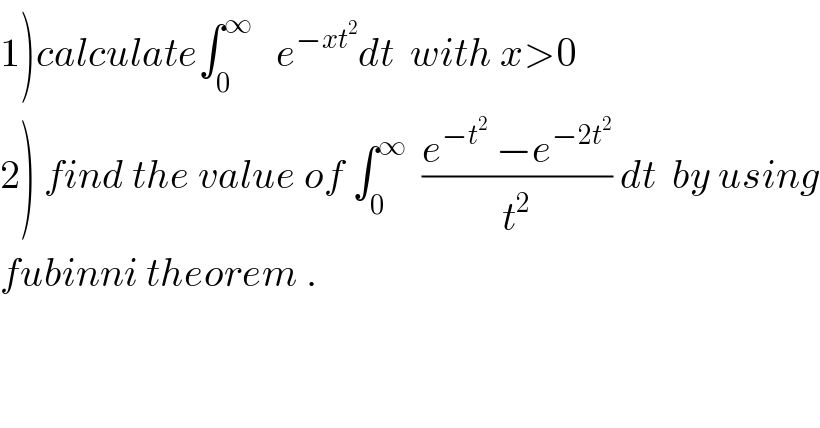 | ||
Commented by maxmathsup by imad last updated on 22/Jan/19 | ||
![1) we have ∫_0 ^∞ e^(−xt^2 ) dt =_(t(√x)=u) ∫_0 ^∞ e^(−u^2 ) (du/(√x)) =(1/(√x)) ∫_0 ^∞ e^(−u^2 ) du =(1/(√x)) ((√π)/2) =((√π)/(2(√x))) 2) we have ∫_1 ^2 ((√π)/(2(√x))) dx =(√π)[(√x)]_1 ^2 =(√π)((√2)−1) but ∫_1 ^2 ((√π)/(2(√x))) dx =∫_1 ^2 (∫_0 ^∞ e^(−xt^2 ) dt)dx =∫_0 ^∞ ( ∫_1 ^2 e^(−xt^2 ) dx)dt (by fubini) =∫_0 ^∞ ( [−(1/t^2 ) e^(−xt^2 ) ]_(x=1) ^(x=2) )dt =∫_0 ^∞ ((e^(−t^2 ) −e^(−2t^2 ) )/t^2 ) dt ⇒ ∫_0 ^∞ ((e^(−t^2 ) −e^(−2t^2 ) )/t^2 ) dt =(√π)((√2)−1)](Q53457.png) | ||
Commented by maxmathsup by imad last updated on 22/Jan/19 | ||
 | ||