
Question and Answers Forum
Question Number 74637 by mathmax by abdo last updated on 28/Nov/19
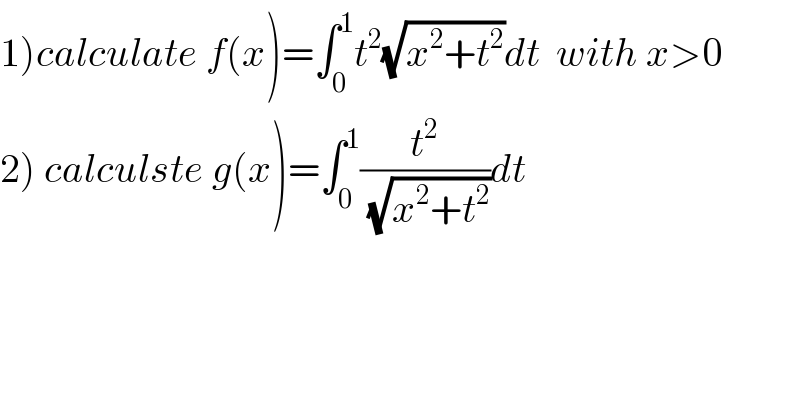
Commented by mathmax by abdo last updated on 28/Nov/19
![1) we have f(x)=∫_0 ^1 t^2 (√(x^2 +t^2 ))dt ⇒f(x)=_(t=x sh(u)) ∫_0 ^(argsh((1/x))) x^2 sh^2 u(xch(u))xch(u)du = x^4 ∫_0 ^(ln((1/x)+(√(1+(1/x^2 ))))) sh^2 (u)ch^2 (u)du =(x^4 /4) ∫_0 ^(ln(((1+(√(x^2 +1)))/x))) sh^2 (2u) du =(x^4 /8) ∫_0 ^(ln(((1+(√(x^2 +1)))/x))) (ch(4u)−1))du =(x^4 /(32))[ sh(4u)]_0 ^(ln(((1+(√(x^2 +1)))/x))) −(x^4 /8)ln(((1+(√(x^2 +1)))/x)) =(x^4 /(64))[e^(4u) −e^(−4u) ]_0 ^(ln(((1+(√(x^2 +1)))/x))) −(x^4 /8)ln(((1+(√(x^2 +1)))/x)) =(x^4 /(64)){(((1+(√(x^2 +1)))/x))^4 −(((1+(√(x^2 +1)))/x))^(−4) }−(x^4 /8)ln(((1+(√(x^2 +1)))/x))](Q74681.png)
Answered by MJS last updated on 28/Nov/19
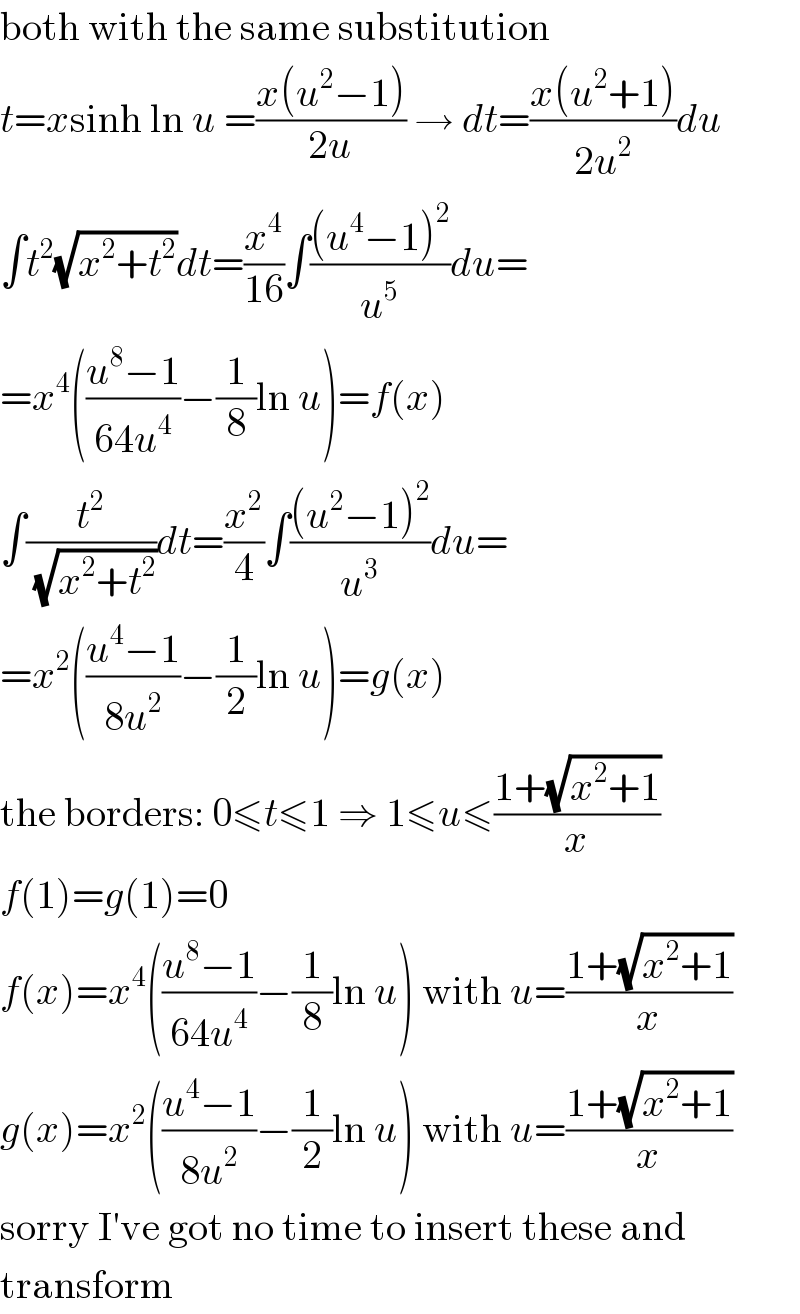
| ||
Question and Answers Forum | ||
Question Number 74637 by mathmax by abdo last updated on 28/Nov/19 | ||
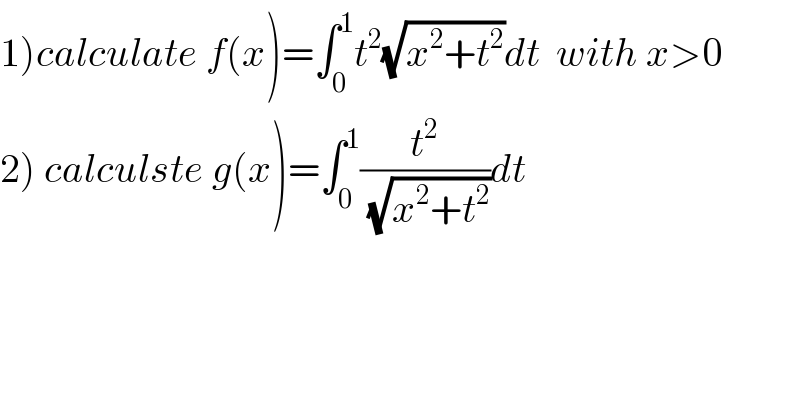 | ||
Commented by mathmax by abdo last updated on 28/Nov/19 | ||
![1) we have f(x)=∫_0 ^1 t^2 (√(x^2 +t^2 ))dt ⇒f(x)=_(t=x sh(u)) ∫_0 ^(argsh((1/x))) x^2 sh^2 u(xch(u))xch(u)du = x^4 ∫_0 ^(ln((1/x)+(√(1+(1/x^2 ))))) sh^2 (u)ch^2 (u)du =(x^4 /4) ∫_0 ^(ln(((1+(√(x^2 +1)))/x))) sh^2 (2u) du =(x^4 /8) ∫_0 ^(ln(((1+(√(x^2 +1)))/x))) (ch(4u)−1))du =(x^4 /(32))[ sh(4u)]_0 ^(ln(((1+(√(x^2 +1)))/x))) −(x^4 /8)ln(((1+(√(x^2 +1)))/x)) =(x^4 /(64))[e^(4u) −e^(−4u) ]_0 ^(ln(((1+(√(x^2 +1)))/x))) −(x^4 /8)ln(((1+(√(x^2 +1)))/x)) =(x^4 /(64)){(((1+(√(x^2 +1)))/x))^4 −(((1+(√(x^2 +1)))/x))^(−4) }−(x^4 /8)ln(((1+(√(x^2 +1)))/x))](Q74681.png) | ||
Answered by MJS last updated on 28/Nov/19 | ||
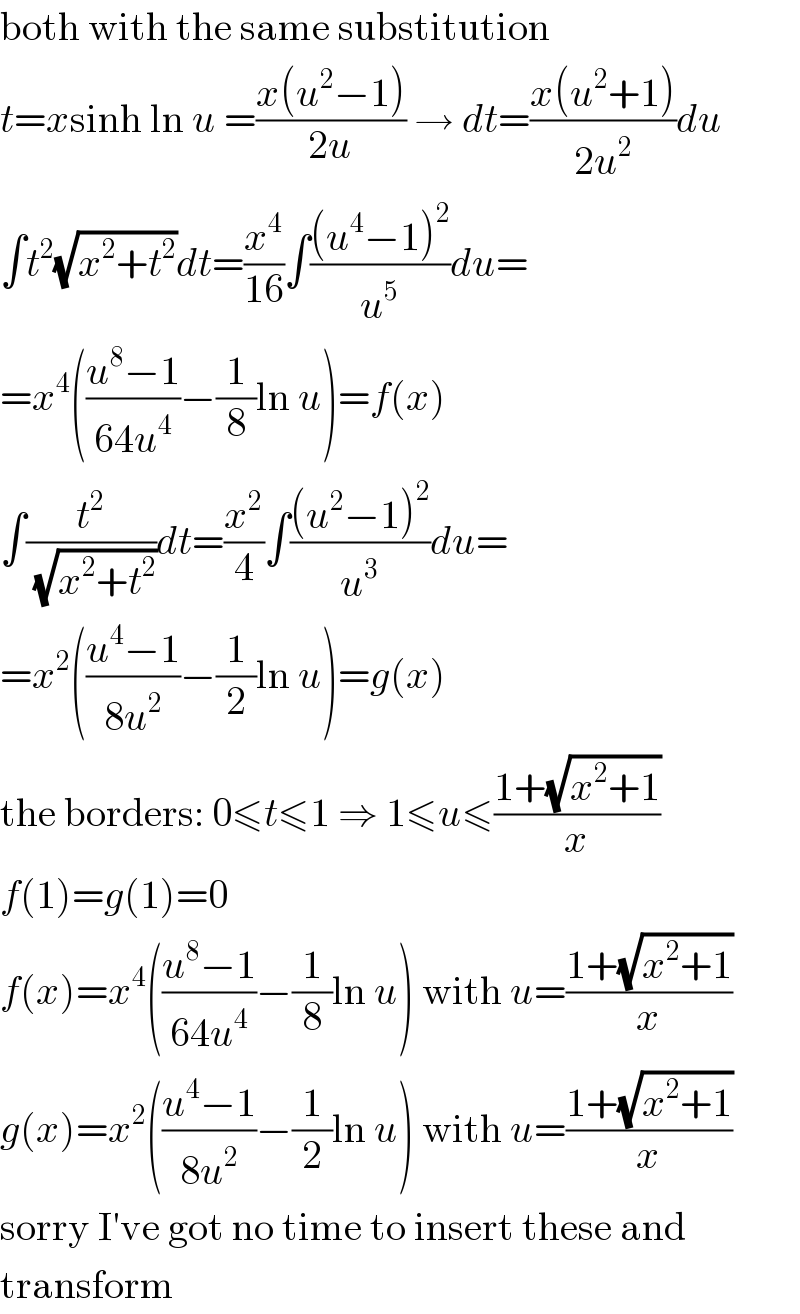 | ||
| ||