
Question and Answers Forum
Question Number 82971 by mathmax by abdo last updated on 26/Feb/20
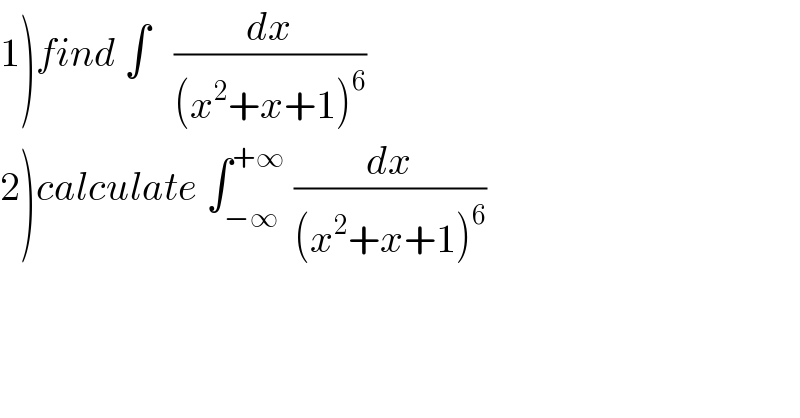
Commented by mathmax by abdo last updated on 26/Feb/20
![2) let A =∫_(−∞) ^(+∞) (dx/((x^2 +x+1)^6 )) ⇒ A =∫_(−∞) ^(+∞) (dx/(((x+(1/2))^2 +(3/4))^6 )) =_(x+(1/2)=((√3)/2)t) ((4/3))^6 ∫_(−∞) ^(+∞) (dt/((t^2 +1)^6 )) let also changement t=tanθ give ∫_(−∞) ^(+∞) (dt/((t^2 +1)^6 )) =∫_(−(π/2)) ^(π/2) (((1+tan^2 θ)dθ)/((1+tan^2 θ)^6 )) =∫_(−(π/2)) ^(π/2) (dθ/((1+tan^2 θ)^4 )) =∫_(−(π/2)) ^(π/2) cos^8 t dt =2 ∫_0 ^(π/2) (((1+cos(2t))/2))^4 dt =(1/8)∫_0 ^(π/2) (1+2cos(2t) +cos^2 (2t))^2 dt =(1/8)∫_0 ^(π/2) { (1+2cos(2t))^2 +2(1+2cos(2t)cos^2 (2t) +cos^4 (2t))dt =(1/8)∫_0 ^(π/2) {1+4cos(2t) +4cos^2 (2t) +2cos^2 (2t)+4cos^3 (2t)+cos^4 (2t)}dt =(π/(16)) +(1/2)∫_0 ^(π/2) cos(2t)+(3/4)∫_0 ^(π/2) cos^2 (2t)dt+(1/2)∫_0 ^(π/2) cos^3 (2t)dt+(1/8)∫_0 ^(π/2) cos^4 (2t)dt ∫_0 ^(π/2) cos(2t)dt =(1/2)sin(2t)]_0 ^(π/2) =0 ∫_0 ^(π/2) cos^2 (2t)dt =(1/2)∫_0 ^(π/2) (1+cos(4t))dt =(π/4) +(1/8)[sin(4t)]_0 ^(π/2) =(π/4) ∫_0 ^(π/2) cos^3 (2t)dt =∫_0 ^(π/2) (((1+cos(4t))/2))cos(2t)dt =(1/2)∫_0 ^(π/2) {cos(2t)+cos(2t)cos(4t)}dt =(1/2)∫_0 ^(π/2) cos(2t)dt +(1/4)∫_0 ^(π/2) (cos(2t)+cos(6t))dt=0 ∫_0 ^(π/2) cos^4 t dt =∫_0 ^(π/2) (((1+cos(2t))/2))^2 dt =(1/4)∫_0 ^(π/2) (1+2cos(2t) +cos^2 (2t))dt =(π/8) +(1/2)∫_0 ^(π/2) cos(2t)dt +(1/8)∫_0 ^(π/2) (1+cos(4t))dt =(π/8) +0+(π/(16)) =((3π)/(16)) the value of I is known](Q83014.png)
Commented by abdomathmax last updated on 26/Feb/20
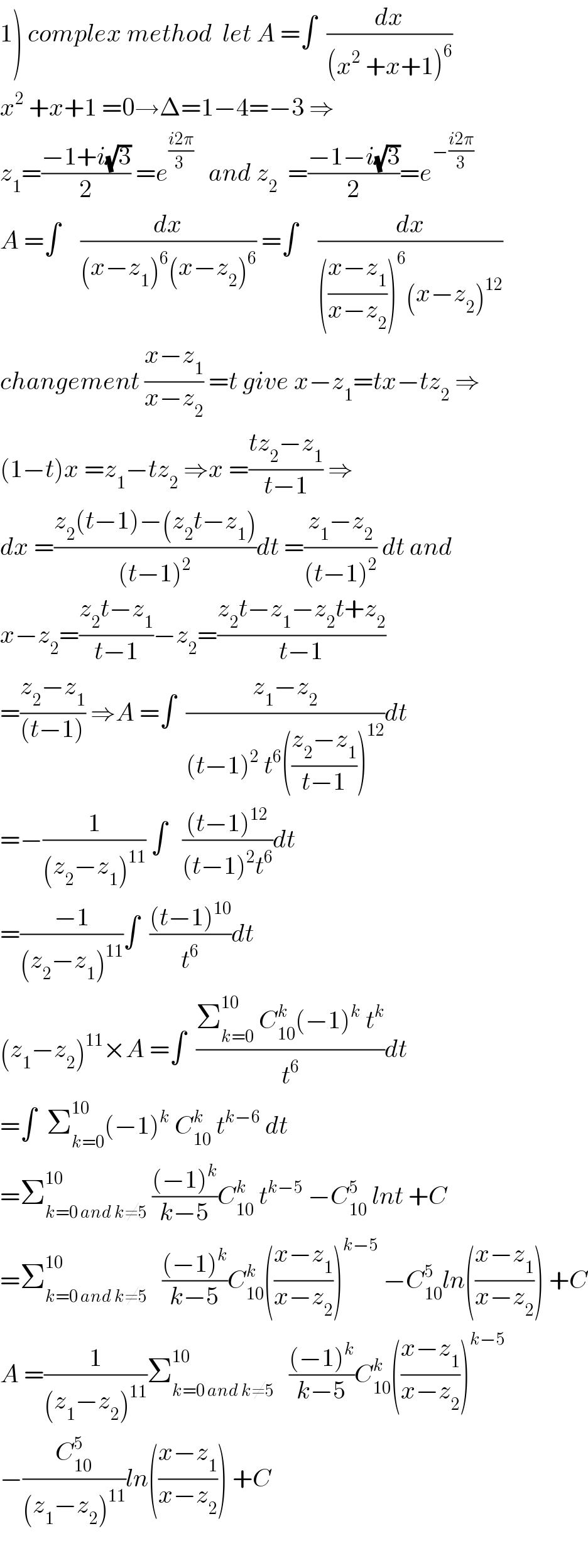
Answered by MJS last updated on 26/Feb/20

| ||
Question and Answers Forum | ||
Question Number 82971 by mathmax by abdo last updated on 26/Feb/20 | ||
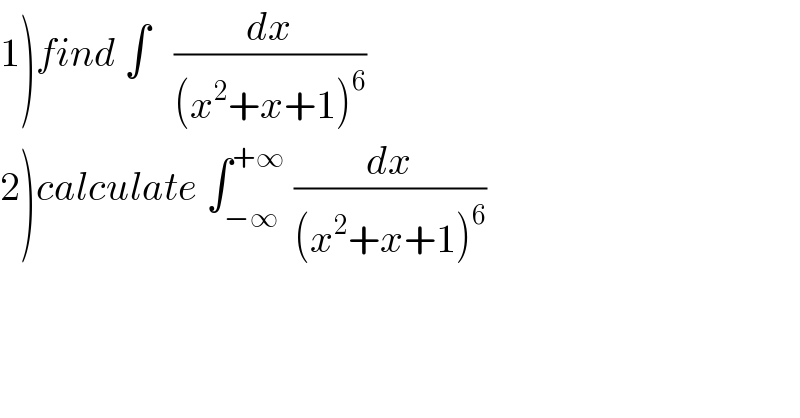 | ||
Commented by mathmax by abdo last updated on 26/Feb/20 | ||
![2) let A =∫_(−∞) ^(+∞) (dx/((x^2 +x+1)^6 )) ⇒ A =∫_(−∞) ^(+∞) (dx/(((x+(1/2))^2 +(3/4))^6 )) =_(x+(1/2)=((√3)/2)t) ((4/3))^6 ∫_(−∞) ^(+∞) (dt/((t^2 +1)^6 )) let also changement t=tanθ give ∫_(−∞) ^(+∞) (dt/((t^2 +1)^6 )) =∫_(−(π/2)) ^(π/2) (((1+tan^2 θ)dθ)/((1+tan^2 θ)^6 )) =∫_(−(π/2)) ^(π/2) (dθ/((1+tan^2 θ)^4 )) =∫_(−(π/2)) ^(π/2) cos^8 t dt =2 ∫_0 ^(π/2) (((1+cos(2t))/2))^4 dt =(1/8)∫_0 ^(π/2) (1+2cos(2t) +cos^2 (2t))^2 dt =(1/8)∫_0 ^(π/2) { (1+2cos(2t))^2 +2(1+2cos(2t)cos^2 (2t) +cos^4 (2t))dt =(1/8)∫_0 ^(π/2) {1+4cos(2t) +4cos^2 (2t) +2cos^2 (2t)+4cos^3 (2t)+cos^4 (2t)}dt =(π/(16)) +(1/2)∫_0 ^(π/2) cos(2t)+(3/4)∫_0 ^(π/2) cos^2 (2t)dt+(1/2)∫_0 ^(π/2) cos^3 (2t)dt+(1/8)∫_0 ^(π/2) cos^4 (2t)dt ∫_0 ^(π/2) cos(2t)dt =(1/2)sin(2t)]_0 ^(π/2) =0 ∫_0 ^(π/2) cos^2 (2t)dt =(1/2)∫_0 ^(π/2) (1+cos(4t))dt =(π/4) +(1/8)[sin(4t)]_0 ^(π/2) =(π/4) ∫_0 ^(π/2) cos^3 (2t)dt =∫_0 ^(π/2) (((1+cos(4t))/2))cos(2t)dt =(1/2)∫_0 ^(π/2) {cos(2t)+cos(2t)cos(4t)}dt =(1/2)∫_0 ^(π/2) cos(2t)dt +(1/4)∫_0 ^(π/2) (cos(2t)+cos(6t))dt=0 ∫_0 ^(π/2) cos^4 t dt =∫_0 ^(π/2) (((1+cos(2t))/2))^2 dt =(1/4)∫_0 ^(π/2) (1+2cos(2t) +cos^2 (2t))dt =(π/8) +(1/2)∫_0 ^(π/2) cos(2t)dt +(1/8)∫_0 ^(π/2) (1+cos(4t))dt =(π/8) +0+(π/(16)) =((3π)/(16)) the value of I is known](Q83014.png) | ||
Commented by abdomathmax last updated on 26/Feb/20 | ||
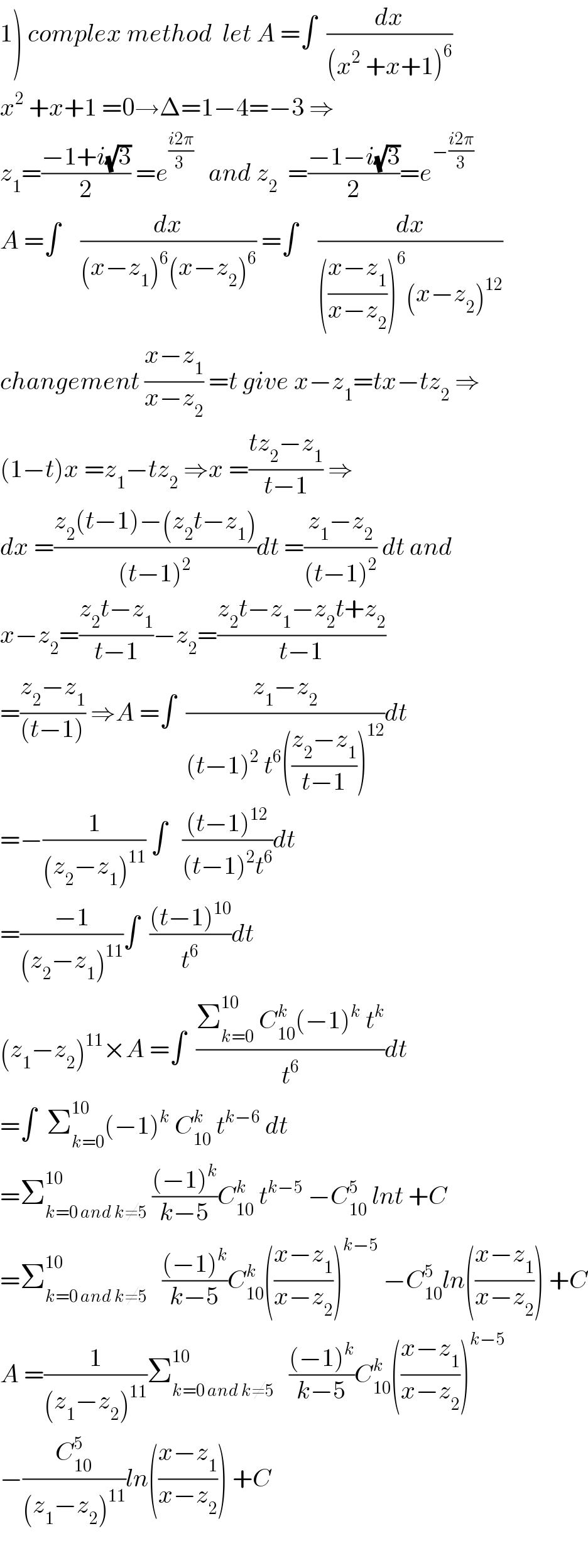 | ||
Answered by MJS last updated on 26/Feb/20 | ||
 | ||
| ||