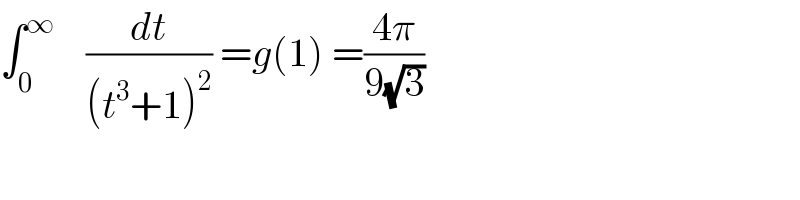Question and Answers Forum
Question Number 65288 by mathmax by abdo last updated on 27/Jul/19
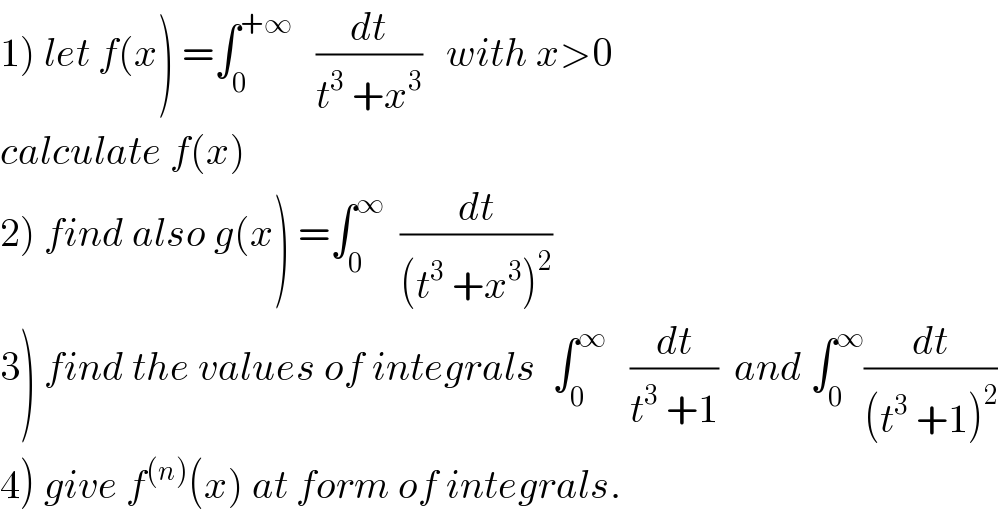
Commented by mathmax by abdo last updated on 30/Jul/19
![1) f(x)=∫_0 ^∞ (dt/(t^3 +x^3 ))dt ⇒f(x) =∫_0 ^∞ (dt/((t+x)(t^2 −xt +x^2 ))) let decompose F(t) =(1/((t+x)(t^2 −xt +x^2 ))) F(t) =(a/(t+x)) +((bt +c)/(t^2 −xt +x^2 )) (x>0) a =lim_(t→−x) (t+x)F(t) =(1/(3x^2 )) lim_(t→+∞) tF(t) =0 =a+b ⇒b =−(1/(3x^2 )) ⇒F(t)=(1/(3x^2 (t+x))) +((−(1/(3x^2 ))t+c)/(t^2 −xt+x^2 )) F(0) =(1/x^3 ) =(1/(3x^3 )) +(c/x^2 ) ⇒c =0 ⇒1=(1/3) +xc ⇒xc =(2/3) ⇒c =(2/(3x)) ⇒ F(t) =(1/(3x^2 (t+x))) +((−(t/(3x^2 ))+(2/(3x)))/(t^2 −xt+x^2 )) =(1/(3x^2 (t+x)))−(1/(3x^2 )) ((t−2x)/(t^2 −xt +x^2 )) ⇒ f(x) =(1/(3x^2 )){ ∫_0 ^∞ (dt/(t+x)) −∫_0 ^∞ ((t−2x)/(t^2 −xt +x^2 ))} =(1/(3x^2 )){ ∫_0 ^∞ (dt/(t+x)) −(1/2)∫_0 ^∞ ((2t−x+x)/(t^2 −xt +x^2 )) +∫_0 ^∞ ((2x)/(t^2 −xt+x^2 ))dt} =(1/(3x^2 )){ [ln∣((t+x)/(√(t^2 −xt+x^2 )))∣]_0 ^(+∞) +((3x)/2)∫_0 ^∞ (dt/(t^2 −xt +x^2 ))} =(1/(2x))∫_0 ^∞ (dt/(t^2 −xt +x^2 )) and ∫_0 ^∞ (dt/(t^2 −xt +x^2 )) =∫_0 ^∞ (dt/(t^2 −2(x/2)t +(x^2 /4)+x^2 −(x^2 /4))) =∫_0 ^∞ (dt/((t−(x/2))^2 +(3/4)x^2 )) =_(t−(x/2)=((√3)/2)xu) ∫_(−(1/(√3))) ^(+∞) (1/((3/4)x^2 (1+u^2 )))((√3)/2) xdu =(4/(3x^2 )) ((√3)/2) x ∫_(−(1/(√3))) ^(+∞) (du/(1+u^2 )) =(2/(x(√3)))[arctan(u)]_(−(1/(√3))) ^(+∞) =(2/(x(√3))){(π/2) +arctan((1/(√3)))} =(2/(x(√3))){π −arctan((√3)) =(2/(x(√3))){π−(π/3)} =(2/(x(√3)))((2π)/3) =((4π)/(3x(√3))) ⇒f(x)=(1/(2x)) ((4π)/(3x(√3))) =((2π)/(3x^2 (√3))) ⇒ f(x) =((2π)/(3(√3)x^2 )) (x>0)](Q65456.png)
Commented by mathmax by abdo last updated on 30/Jul/19
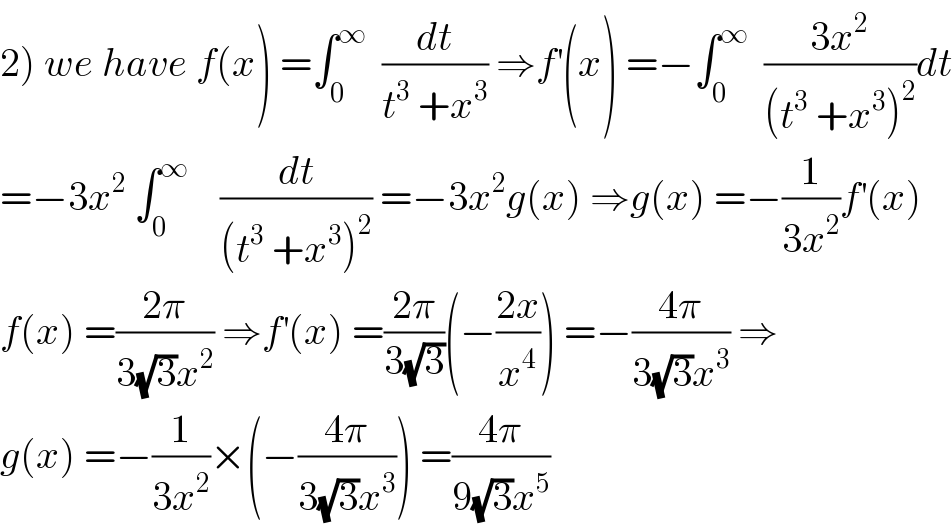
Commented by mathmax by abdo last updated on 30/Jul/19
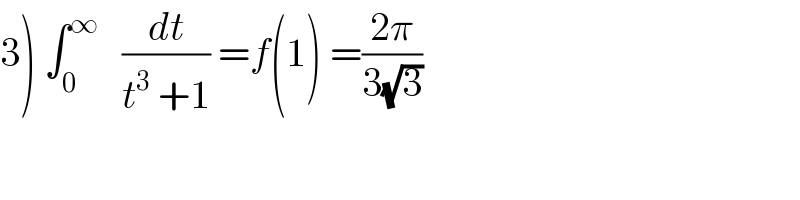
Commented by mathmax by abdo last updated on 30/Jul/19