Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 100146 by ajfour last updated on 25/Jun/20

Commented by bemath last updated on 25/Jun/20

t = ((c^2 −2b−1)/(2(b+1)))

$$\:\:\:\:\:\:\mathrm{t}\:=\:\frac{\mathrm{c}^{\mathrm{2}} −\mathrm{2b}−\mathrm{1}}{\mathrm{2}\left(\mathrm{b}+\mathrm{1}\right)} \\ $$

Commented by ajfour last updated on 25/Jun/20

clearly (√(b+t))=(c/t) or (b+t)t^2 = c^2 let me check (b+((c^2 −2b−1)/(2(b+1))))[((c^2 −2b−1)/(2(b+1)))]^2 ≠ c^2 please check your answer sir, or post your workings..

$${clearly}\:\:\sqrt{{b}+{t}}=\frac{{c}}{{t}} \\ $$$${or}\:\:\:\left({b}+{t}\right){t}^{\mathrm{2}} =\:{c}^{\mathrm{2}} \\ $$$${let}\:{me}\:{check} \\ $$$$\:\:\:\left({b}+\frac{{c}^{\mathrm{2}} −\mathrm{2}{b}−\mathrm{1}}{\mathrm{2}\left({b}+\mathrm{1}\right)}\right)\left[\frac{{c}^{\mathrm{2}} −\mathrm{2}{b}−\mathrm{1}}{\mathrm{2}\left({b}+\mathrm{1}\right)}\right]^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\neq\:{c}^{\mathrm{2}} \\ $$$${please}\:{check}\:{your}\:{answer}\:{sir}, \\ $$$${or}\:{post}\:{your}\:{workings}.. \\ $$

Commented by ajfour last updated on 25/Jun/20

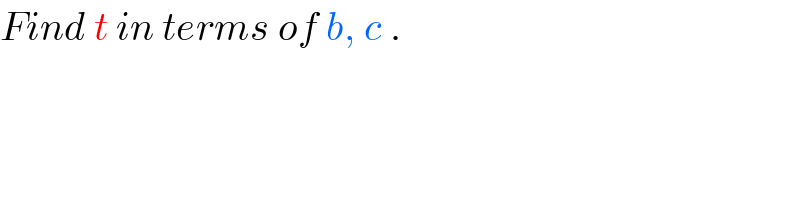
Find t in terms of b, c .

$${Find}\:{t}\:{in}\:{terms}\:{of}\:{b},\:{c}\:. \\ $$

Answered by mr W last updated on 25/Jun/20

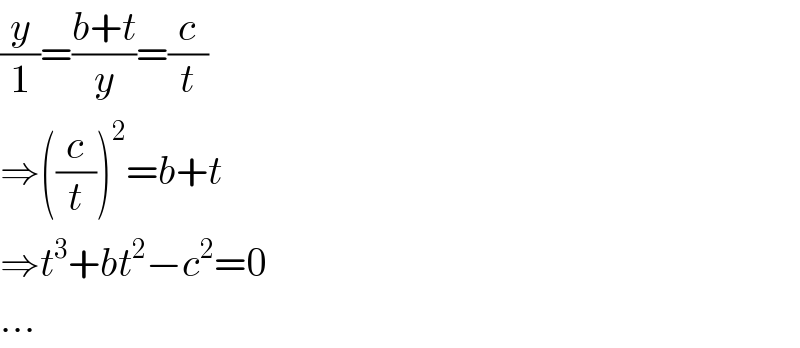
(y/1)=((b+t)/y)=(c/t) ⇒((c/t))^2 =b+t ⇒t^3 +bt^2 −c^2 =0 ...

$$\frac{{y}}{\mathrm{1}}=\frac{{b}+{t}}{{y}}=\frac{{c}}{{t}} \\ $$$$\Rightarrow\left(\frac{{c}}{{t}}\right)^{\mathrm{2}} ={b}+{t} \\ $$$$\Rightarrow{t}^{\mathrm{3}} +{bt}^{\mathrm{2}} −{c}^{\mathrm{2}} =\mathrm{0} \\ $$$$... \\ $$

Commented by ajfour last updated on 25/Jun/20

thanls sir, i hope someday some geometry shall pave the way..!

$${thanls}\:{sir},\:{i}\:{hope}\:{someday} \\ $$$${some}\:{geometry}\:{shall}\:{pave}\:{the} \\ $$$${way}..! \\ $$

Commented by bemath last updated on 25/Jun/20

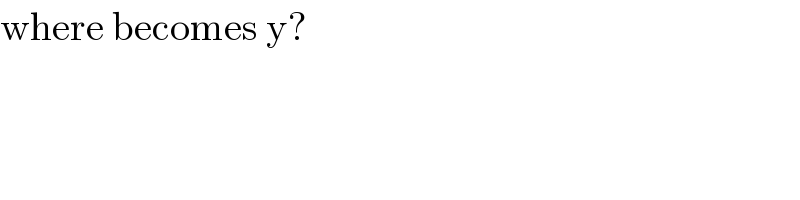
where becomes y?

$$\mathrm{where}\:\mathrm{becomes}\:\mathrm{y}? \\ $$

Commented by 1549442205 last updated on 25/Jun/20

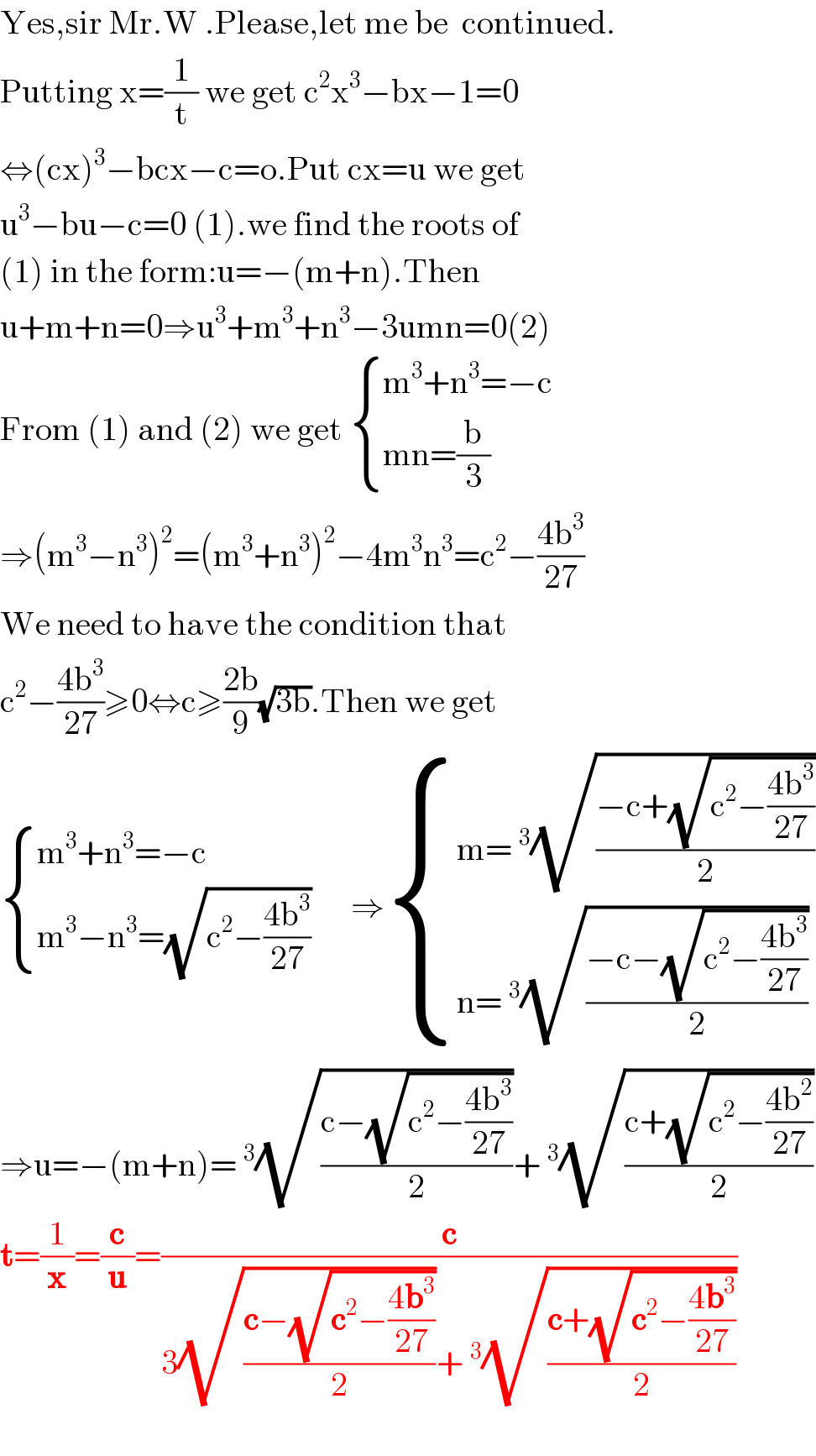
Yes,sir Mr.W .Please,let me be continued. Putting x=(1/t) we get c^2 x^3 −bx−1=0 ⇔(cx)^3 −bcx−c=o.Put cx=u we get u^3 −bu−c=0 (1).we find the roots of (1) in the form:u=−(m+n).Then u+m+n=0⇒u^3 +m^3 +n^3 −3umn=0(2) From (1) and (2) we get { ((m^3 +n^3 =−c)),((mn=(b/3))) :} ⇒(m^3 −n^3 )^2 =(m^3 +n^3 )^2 −4m^3 n^3 =c^2 −((4b^3 )/(27)) We need to have the condition that c^2 −((4b^3 )/(27))≥0⇔c≥((2b)/9)(√(3b)).Then we get { ((m^3 +n^3 =−c)),((m^3 −n^3 =(√(c^2 −((4b^3 )/(27)))))) :} ⇒ { ((m=^3 (√((−c+(√(c^2 −((4b^3 )/(27)))))/2)))),((n=^3 (√((−c−(√(c^2 −((4b^3 )/(27)))))/2)))) :} ⇒u=−(m+n)=^3 (√((c−(√(c^2 −((4b^3 )/(27)))))/2))+^3 (√((c+(√(c^2 −((4b^2 )/(27)))))/2)) t=(1/x)=(c/u)=(c/(3(√((c−(√(c^2 −((4b^3 )/(27)))))/2))+^3 (√((c+(√(c^2 −((4b^3 )/(27)))))/2))))

$$\mathrm{Yes},\mathrm{sir}\:\mathrm{Mr}.\mathrm{W}\:.\mathrm{Please},\mathrm{let}\:\mathrm{me}\:\mathrm{be}\:\:\mathrm{continued}. \\ $$$$\mathrm{Putting}\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}\:\mathrm{we}\:\mathrm{get}\:\mathrm{c}^{\mathrm{2}} \mathrm{x}^{\mathrm{3}} −\mathrm{bx}−\mathrm{1}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{cx}\right)^{\mathrm{3}} −\mathrm{bcx}−\mathrm{c}=\mathrm{o}.\mathrm{Put}\:\mathrm{cx}=\mathrm{u}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{u}^{\mathrm{3}} −\mathrm{bu}−\mathrm{c}=\mathrm{0}\:\left(\mathrm{1}\right).\mathrm{we}\:\mathrm{find}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\: \\ $$$$\left(\mathrm{1}\right)\:\mathrm{in}\:\mathrm{the}\:\mathrm{form}:\mathrm{u}=−\left(\mathrm{m}+\mathrm{n}\right).\mathrm{Then} \\ $$$$\mathrm{u}+\mathrm{m}+\mathrm{n}=\mathrm{0}\Rightarrow\mathrm{u}^{\mathrm{3}} +\mathrm{m}^{\mathrm{3}} +\mathrm{n}^{\mathrm{3}} −\mathrm{3umn}=\mathrm{0}\left(\mathrm{2}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{get}\:\begin{cases}{\mathrm{m}^{\mathrm{3}} +\mathrm{n}^{\mathrm{3}} =−\mathrm{c}}\\{\mathrm{mn}=\frac{\mathrm{b}}{\mathrm{3}}}\end{cases} \\ $$$$\Rightarrow\left(\mathrm{m}^{\mathrm{3}} −\mathrm{n}^{\mathrm{3}} \right)^{\mathrm{2}} =\left(\mathrm{m}^{\mathrm{3}} +\mathrm{n}^{\mathrm{3}} \right)^{\mathrm{2}} −\mathrm{4m}^{\mathrm{3}} \mathrm{n}^{\mathrm{3}} =\mathrm{c}^{\mathrm{2}} −\frac{\mathrm{4b}^{\mathrm{3}} }{\mathrm{27}} \\ $$$$\mathrm{We}\:\mathrm{need}\:\mathrm{to}\:\mathrm{have}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{that} \\ $$$$\mathrm{c}^{\mathrm{2}} −\frac{\mathrm{4b}^{\mathrm{3}} }{\mathrm{27}}\geqslant\mathrm{0}\Leftrightarrow\mathrm{c}\geqslant\frac{\mathrm{2b}}{\mathrm{9}}\sqrt{\mathrm{3b}}.\mathrm{Then}\:\mathrm{we}\:\mathrm{get} \\ $$$$\begin{cases}{\mathrm{m}^{\mathrm{3}} +\mathrm{n}^{\mathrm{3}} =−\mathrm{c}}\\{\mathrm{m}^{\mathrm{3}} −\mathrm{n}^{\mathrm{3}} =\sqrt{\mathrm{c}^{\mathrm{2}} −\frac{\mathrm{4b}^{\mathrm{3}} }{\mathrm{27}}}}\end{cases}\:\:\:\:\:\:\Rightarrow\begin{cases}{\mathrm{m}=\:^{\mathrm{3}} \sqrt{\frac{−\mathrm{c}+\sqrt{\mathrm{c}^{\mathrm{2}} −\frac{\mathrm{4b}^{\mathrm{3}} }{\mathrm{27}}}}{\mathrm{2}}}}\\{\mathrm{n}=\:^{\mathrm{3}} \sqrt{\frac{−\mathrm{c}−\sqrt{\mathrm{c}^{\mathrm{2}} −\frac{\mathrm{4b}^{\mathrm{3}} }{\mathrm{27}}}}{\mathrm{2}}}}\end{cases} \\ $$$$\Rightarrow\mathrm{u}=−\left(\mathrm{m}+\mathrm{n}\right)=\:^{\mathrm{3}} \sqrt{\frac{\mathrm{c}−\sqrt{\mathrm{c}^{\mathrm{2}} −\frac{\mathrm{4b}^{\mathrm{3}} }{\mathrm{27}}}}{\mathrm{2}}}+\:^{\mathrm{3}} \sqrt{\frac{\mathrm{c}+\sqrt{\mathrm{c}^{\mathrm{2}} −\frac{\mathrm{4b}^{\mathrm{2}} }{\mathrm{27}}}}{\mathrm{2}}} \\ $$$$\boldsymbol{\mathrm{t}}=\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}=\frac{\boldsymbol{\mathrm{c}}}{\boldsymbol{\mathrm{u}}}=\frac{\boldsymbol{\mathrm{c}}}{\mathrm{3}\sqrt{\frac{\boldsymbol{\mathrm{c}}−\sqrt{\boldsymbol{\mathrm{c}}^{\mathrm{2}} −\frac{\mathrm{4}\boldsymbol{\mathrm{b}}^{\mathrm{3}} }{\mathrm{27}}}}{\mathrm{2}}}+\:^{\mathrm{3}} \sqrt{\frac{\boldsymbol{\mathrm{c}}+\sqrt{\boldsymbol{\mathrm{c}}^{\mathrm{2}} −\frac{\mathrm{4}\boldsymbol{\mathrm{b}}^{\mathrm{3}} }{\mathrm{27}}}}{\mathrm{2}}}} \\ $$$$ \\ $$

Commented by mr W last updated on 25/Jun/20

thank you, very nice sir! i have had applied cardano directly.

$${thank}\:{you},\:{very}\:{nice}\:{sir}! \\ $$$${i}\:{have}\:{had}\:{applied}\:{cardano}\:{directly}. \\ $$

Commented by mr W last updated on 25/Jun/20

Commented by ajfour last updated on 25/Jun/20

thanks ....205 Sir, but cannot we have an answer for any real b amd c ?

$${thanks}\:\:....\mathrm{205}\:{Sir},\:{but}\:{cannot} \\ $$$${we}\:{have}\:{an}\:{answer}\:{for}\:{any} \\ $$$${real}\:{b}\:{amd}\:{c}\:? \\ $$

Commented by 1549442205 last updated on 26/Jun/20

There is always exists some root for the values of b and c so that c^2 ≥((4b^3 )/(27)). Example,b=3,c=4⇒t≈1.821640

$$\mathrm{There}\:\mathrm{is}\:\mathrm{always}\:\mathrm{exists}\:\mathrm{some}\:\mathrm{root}\:\mathrm{for}\: \\ $$$$\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\mathrm{b}\:\mathrm{and}\:\mathrm{c}\:\mathrm{so}\:\mathrm{that}\:\mathrm{c}^{\mathrm{2}} \geqslant\frac{\mathrm{4b}^{\mathrm{3}} }{\mathrm{27}}. \\ $$$$\boldsymbol{\mathrm{Example}},\boldsymbol{\mathrm{b}}=\mathrm{3},\boldsymbol{\mathrm{c}}=\mathrm{4}\Rightarrow\boldsymbol{\mathrm{t}}\approx\mathrm{1}.\mathrm{821640} \\ $$

Commented by 1549442205 last updated on 30/Jun/20

But I want(please get his permission) to do the his work again in...the moment!.!.!

$$\mathrm{But}\:\mathrm{I}\:\mathrm{want}\left(\mathrm{please}\:\mathrm{get}\:\mathrm{his}\:\mathrm{permission}\right)\: \\ $$$$\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{do}}\:\mathrm{the}\:\mathrm{his}\:\mathrm{work}\: \\ $$$$\mathrm{again}\:\mathrm{in}...\mathrm{the}\:\mathrm{moment}!.!.! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com