Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 100223 by DGmichael last updated on 25/Jun/20

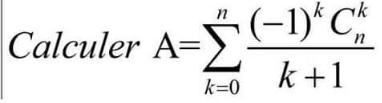
Answered by maths mind last updated on 25/Jun/20

$$A=\underset{k=0}{\sum ^n}\frac{{(-1)}^k{C}_n^k}{k+1}$$$$letf\left(x\right)={(1-x)}^n\Rightarrow f\left(x\right)=\underset{k=0}{\sum ^n}{C}_n^k{(-1)}^k{x}^k$$$${\int }_0^1{(1-x)}^{n}dx={\int }_0^1\underset{k=0}{\sum ^n}{C}_n^k{(-1)}^k{x}^{k}dx$$$$=\underset{k=0}{\sum ^n}{C}_n^k{(-1)}^k{\int }_0^1{x}^{k}dx=\mathrm{\Sigma }{C}_n^k{(-1)}^k.\frac{1}{k+1}$$$$=\underset{k=0}{\sum ^n}\frac{{(-1)}^k{C}_n^k}{k+1}={\int }_0^1{(1-x)}^{n}dx=\frac{1}{1+n}$$

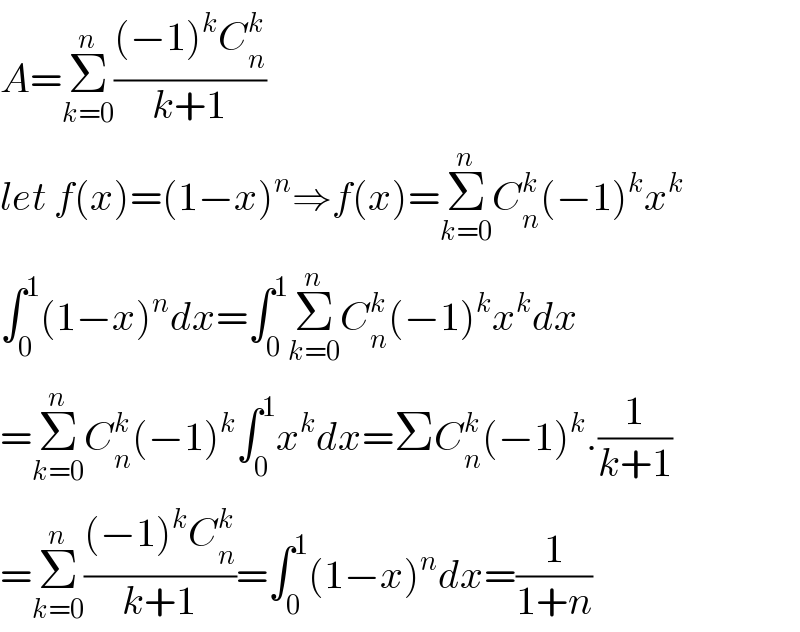
Commented by Ar Brandon last updated on 25/Jun/20

wow amazing ! you quickly recognized the integral.��

Commented by Ar Brandon last updated on 25/Jun/20

Excuse me Sir, Is there any theory for this, or any particular topic that deals with these kind of sums ?

Commented by maths mind last updated on 25/Jun/20

$$themainidea$$$$isnewtoonidentitie$$$${(x+y)}^n=\underset{k=0}{\sum ^n}{C}_n^k{x}^k{y}^{n-k}$$$$thenuseitintegralordifferebtial$$$${\partial }_x{(x+y)}^n={\partial }_x\underset{k=0}{\sum ^n}{C}_n^k{x}^k{y}^{n-k}\iff n{(x+y)}^{n-1}=\sum _{k⩾1}{C}_n^k{kx}^{k-1}{y}^{n-k}$$$$or\frac{{(x+y)}^{n+1}}{n+1}=\mathrm{\Sigma }{C}_n^k\frac{x^{k+1}{y}^{n-k}}{k+1}$$$$exempl$$$$wewant$$$$\underset{k=0}{\sum ^n}\frac{C_n^k}{(k+1)(k+2)(k+3)}...$$$${(1+x)}^n=\underset{k=0}{\sum ^n}{C}_n^k{x}^k\Rightarrow {\int }_0^t{(1+x)}^{n}dx=\mathrm{\Sigma }{\int }_0^t{C}_n^k{x}^{k}dx$$$$\Rightarrow \frac{{(1+t)}^n-1}{n+1}=\underset{k=0}{\sum ^n}\frac{C_n^k{t}^{k+1}}{k+1}$$$${\int }_0^x\frac{{(1+t)}^n-1}{(n+1)}dt=\underset{k=0}{\sum ^n}{C}_n^k{\int }_0^x\frac{t^{k+1}}{(k+1)}dt=\mathrm{\Sigma }{C}_n^k\frac{x^{k+2}}{(k+1)(k+2)}$$$$\frac{{(1+x)}^{n+2}}{(n+1)(n+2)}-\frac{x}{n+1}=\mathrm{\Sigma }{C}_n^k\frac{x^{k+2}}{(k+1)(k+2)}$$$$\Rightarrow {\int }_0^y\frac{{(1+x)}^{n+2}}{(n+1)(n+2)}-\frac{x}{n+1}=\mathrm{\Sigma }{C}_n^k{\int }_0^y\frac{x^{k+2}}{(k+1)(k+2)}$$$$\iff \frac{{(1+y)}^{n+3}}{(n+1)(n+2)(n+3)}-\frac{1}{(n+1)(\mathrm{n}+2)}-\frac{y^2}{2(n+1)}=\underset{k=0}{\sum ^n}{C}_n^k\frac{y^{k+3}}{(k+2)(k+1)(k+3)}$$$$y=1\iff \frac{2^{n+3}}{(n+1)(n+2)(n+3)}-\frac{1}{(\mathrm{n}+1)(\mathrm{n}+2)}-\frac{1}{2(n+1)}=\underset{k=0}{\sum ^n}{C}_n^k.\frac{1}{(k+1)(k+2)(k+3)}$$$$wecanShow$$$$\underset{k=0}{\sum ^n}\frac{C_n^k}{\underset{b=1}{\prod ^r}(k+b)}=\frac{2^{r+n}}{(n+1).....(n+r)}-\underset{j=1}{\sum ^{r-1}}\frac{1}{(r-j)!\underset{k=1}{\prod ^j}(n+j)}$$$$$$

Commented by Ar Brandon last updated on 26/Jun/20

Thanks a lot for your time Sir��

Commented by DGmichael last updated on 26/Jun/20

�� thanks dear sir!

Terms of Service

Privacy Policy

Contact: info@tinkutara.com