Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 100368 by bemath last updated on 26/Jun/20

$$\underset{\mathrm{n}\to \mathrm{\infty }}{\lim }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\cos \left(x^n\right)dx=?$$$$wheren=2k,k\in \mathbb{N},k\ne 0$$

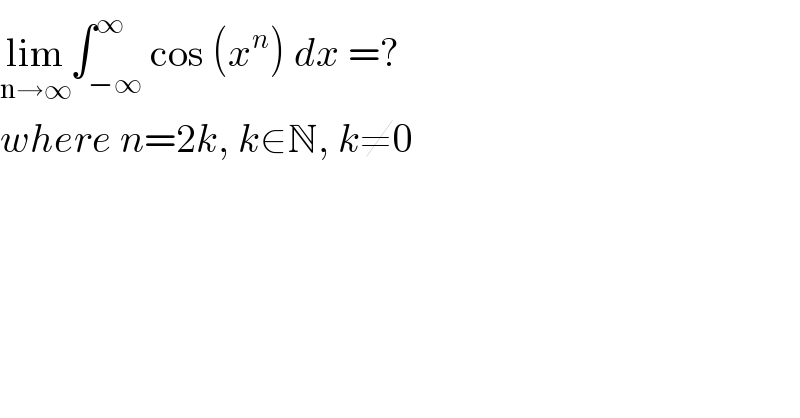
Answered by mathmax by abdo last updated on 26/Jun/20

$${\mathrm{A}}_{\mathrm{n}}={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\cos \left({\mathrm{x}}^{2\mathrm{n}}\right)\mathrm{dx}\Rightarrow {\mathrm{A}}_{\mathrm{n}}=2{\int }_0^{\mathrm{\infty }}\cos \left({\mathrm{x}}^{2\mathrm{n}}\right)\mathrm{dx}=2\mathrm{Re}\left({\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-{\mathrm{ix}}^{2\mathrm{n}}}\mathrm{dx}\right)\mathrm{but}$$$$\mathrm{changement}{\mathrm{ix}}^{2\mathrm{n}}=\mathrm{t}\mathrm{give}{\mathrm{x}}^{2\mathrm{n}}=\frac{\mathrm{t}}{\mathrm{i}}=-\mathrm{it}={\mathrm{e}}^{-\frac{\mathrm{i}\pi }{2}}\mathrm{t}\Rightarrow \mathrm{x}={\left({\mathrm{e}}^{-\frac{\mathrm{i}\pi }{2}}\mathrm{t}\right)}^{\frac{1}{2\mathrm{n}}}$$$$={\mathrm{e}}^{-\frac{\mathrm{i}\pi }{4\mathrm{n}}}{\mathrm{t}}^{\frac{1}{2\mathrm{n}}}\Rightarrow {\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-{\mathrm{ix}}^{2\mathrm{n}}}\mathrm{dx}={\mathrm{e}}^{-\frac{\mathrm{i}\pi }{4\mathrm{n}}}{\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-\mathrm{t}}\frac{1}{2\mathrm{n}}{\mathrm{t}}^{\frac{1}{2\mathrm{n}}-1}\mathrm{dt}$$$$=\frac{{\mathrm{e}}^{-\frac{\mathrm{i}\pi }{4\mathrm{n}}}}{2\mathrm{n}}{\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-\mathrm{t}}{\mathrm{t}}^{\frac{1}{2\mathrm{n}}-1}\mathrm{dt}=\frac{\mathrm{\Gamma }\left(\frac{1}{2\mathrm{n}}\right)}{2\mathrm{n}}\times {\mathrm{e}}^{-\frac{\mathrm{i}\pi }{4\mathrm{n}}}\Rightarrow {\mathrm{A}}_{\mathrm{n}}=2\times \frac{\mathrm{\Gamma }\left(\frac{1}{2\mathrm{n}}\right)}{2\mathrm{n}}\times \cos \left(\frac{\pi }{4\mathrm{n}}\right)\Rightarrow$$$${\mathrm{A}}_{\mathrm{n}}=\frac{1}{\mathrm{n}}\mathrm{\Gamma }\left(\frac{1}{2\mathrm{n}}\right)\cos \left(\frac{\pi }{4\mathrm{n}}\right)\mathrm{rest}\mathrm{to}\mathrm{find}{\lim }_{\mathrm{n}\to +\mathrm{\infty }}{\mathrm{A}}_{\mathrm{n}}....\mathrm{be}\mathrm{continued}...$$$$$$

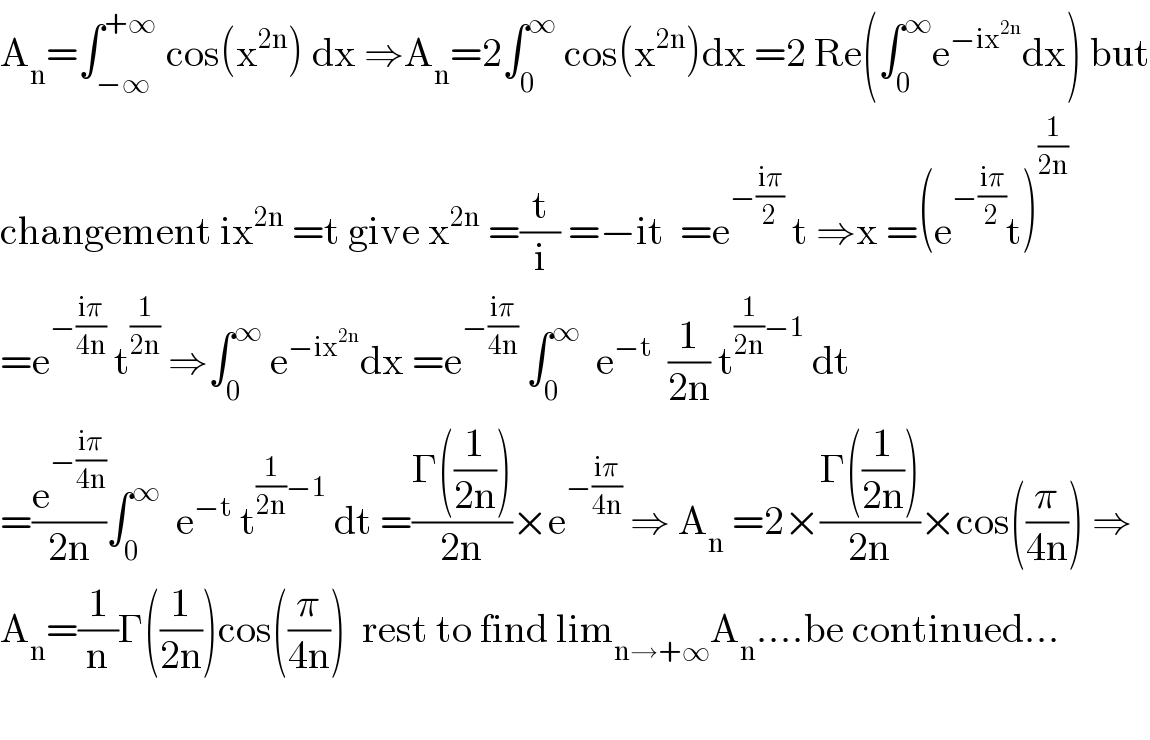
Commented by mathmax by abdo last updated on 26/Jun/20

$$\mathrm{thnk}\mathrm{you}\mathrm{sir}.$$

Commented by Ar Brandon last updated on 26/Jun/20

wow, cool !

Commented by maths mind last updated on 26/Jun/20

$$nicesiricomplet\mathrm{\Gamma }\left(\frac{1}{2n}\right)=\frac{\pi }{\mathrm{\Gamma }(1-\frac{1}{2n})sin\left(\frac{\pi }{2n}\right)}$$$$A_n=\frac{1}{n}\frac{.\pi }{\mathrm{\Gamma }(1-\frac{1}{2n})sin\left(\frac{\pi }{2n}\right)}cos\left(\frac{\pi }{4n}\right),\frac{1}{n}=t$$$$\Rightarrow A_n=\frac{\pi t}{\mathrm{\Gamma }(1-\frac{t}{2})sin\left(\frac{\pi t}{2}\right)}cos\left(\frac{\pi }{4}t\right)$$$$\underset{t\to 0}{\lim }\frac{\pi t}{sin\left(\frac{\pi t}{2}\right)}=\frac{2}{\pi },weget\frac{2}{\pi \mathrm{\Gamma }\left(1\right)}cos\left(0\right)=\frac{2}{\pi }$$$$$$

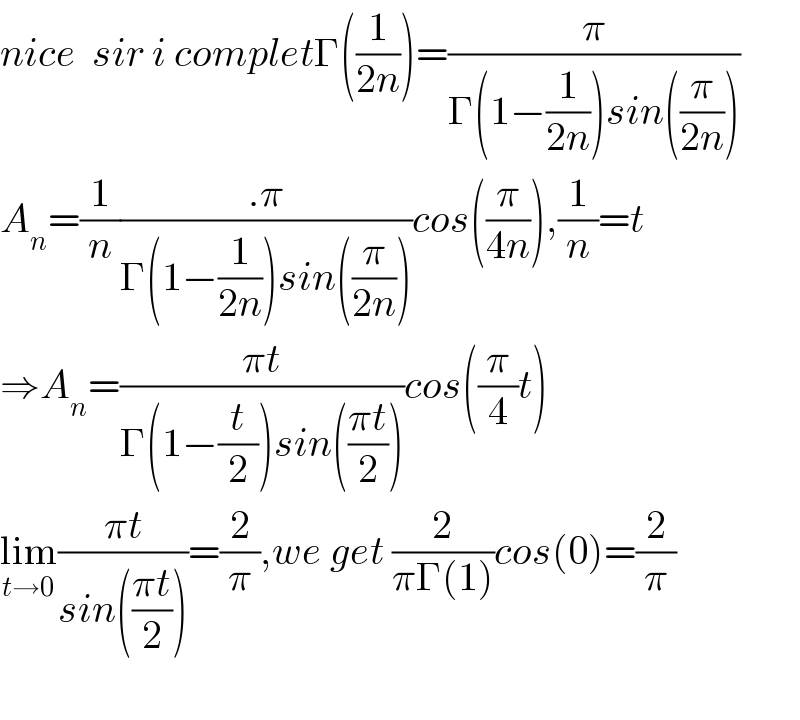
Commented by Ar Brandon last updated on 27/Jun/20

Are you talking to yourself, Sir ?��

Commented by mathmax by abdo last updated on 27/Jun/20

$$\mathrm{i}\mathrm{talk}\mathrm{to}\mathrm{sir}\mathrm{mind}\mathrm{what}\mathrm{happen}\mathrm{to}\mathrm{you}...$$

Commented by Ar Brandon last updated on 27/Jun/20

Oh sorry ! �� I just feel you both are alike. ����

Commented by maths mind last updated on 27/Jun/20

$$withepleasursir$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com