Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 100444 by mr W last updated on 26/Jun/20

Find the number of five−digit numbers containing exactly three different digits? Examples: 12312, 12224

$${Find}\:{the}\:{number}\:{of}\:{five}−{digit}\:{numbers} \\ $$$${containing}\:{exactly}\:{three}\:{different} \\ $$$${digits}?\:{Examples}:\:\mathrm{12312},\:\mathrm{12224} \\ $$

Answered by Rasheed.Sindhi last updated on 28/Jun/20

^• Let a,b,c are digits different from eachother. ^• First digit (from left): a ^• First two digits: a→aa ab (2nd digit may be same or different) ^• First three digits: aa→aaa aab ab→aba abb abc ^• First four digits: aaa→aaab aab→aaba aabb aabc aba→abaa abab abac abb→abba abbb abbc abc→abca abcb abcc ^• Five digits(all possible cases) aaab→aaabc aaba→aabac aabb→aabbc aabc→aabca aabcb aabcc abaa→abaac abab→ababc abac→abaca abacb abacc abba→abbac abbb→abbbc abbc→abbca abbcb abbcc abca→abcaa abcab abcac abcb→abcba abcbb abcbc abcc→abcca abccb abccc Total possible cases 25 ★In each case: (let U={0,1,...,9}) ^• first a can be filled in (U−{0}) 9 ways ^• first b (from left) can be filled in (U−{a}) 9 ways ^• first c (from left) can be filled in (U−{a,b}) 8 ways ^• each of other a′s,b′s,c′s can be filled in 1 way Total ways in each case 9×9×8=648 Total of 25 cases: 648×25=16200

$$\:^{\bullet} {Let}\:{a},{b},{c}\:{are}\:{digits}\:{different}\: \\ $$$$\:\:\:\:{from}\:{eachother}. \\ $$$$\:^{\bullet} {First}\:{digit}\:\left({from}\:{left}\right):\:{a} \\ $$$$\:^{\bullet} {First}\:{two}\:{digits}:\:{a}\rightarrow{aa}\:{ab} \\ $$$$\:\:\:\left(\mathrm{2}{nd}\:{digit}\:{may}\:{be}\:{same}\:{or}\:{different}\right) \\ $$$$\:^{\bullet} {First}\:{three}\:{digits}: \\ $$$$\:\:\:{aa}\rightarrow{aaa}\:{aab} \\ $$$$\:\:{ab}\rightarrow{aba}\:{abb}\:{abc} \\ $$$$\:^{\bullet} {First}\:{four}\:{digits}: \\ $$$$\:{aaa}\rightarrow{aaab} \\ $$$$\:{aab}\rightarrow{aaba}\:{aabb}\:{aabc} \\ $$$$\:{aba}\rightarrow{abaa}\:{abab}\:{abac} \\ $$$$\:{abb}\rightarrow{abba}\:{abbb}\:{abbc} \\ $$$$\:{abc}\rightarrow{abca}\:{abcb}\:{abcc} \\ $$$$\:^{\bullet} {Five}\:{digits}\left({all}\:{possible}\:{cases}\right) \\ $$$$\:\:\:{aaab}\rightarrow{aaabc} \\ $$$$ \\ $$$$\:\:\:{aaba}\rightarrow{aabac} \\ $$$$\:\:\:{aabb}\rightarrow{aabbc}\: \\ $$$$\:\:\:{aabc}\rightarrow{aabca}\:{aabcb}\:{aabcc} \\ $$$$ \\ $$$$\:\:\:{abaa}\rightarrow{abaac} \\ $$$$\:\:\:{abab}\rightarrow{ababc} \\ $$$$\:\:\:{abac}\rightarrow{abaca}\:{abacb}\:{abacc} \\ $$$$\: \\ $$$$\:\:{abba}\rightarrow{abbac} \\ $$$$\:\:{abbb}\rightarrow{abbbc} \\ $$$$\:\:{abbc}\rightarrow{abbca}\:{abbcb}\:{abbcc} \\ $$$$ \\ $$$$\:\:{abca}\rightarrow{abcaa}\:{abcab}\:{abcac} \\ $$$$\:\:{abcb}\rightarrow{abcba}\:{abcbb}\:{abcbc} \\ $$$$\:\:{abcc}\rightarrow{abcca}\:{abccb}\:{abccc} \\ $$$$ \\ $$$${Total}\:{possible}\:{cases}\:\mathrm{25} \\ $$$$\:\bigstar{In}\:{each}\:{case}: \\ $$$$\:\:\left({let}\:\mathrm{U}=\left\{\mathrm{0},\mathrm{1},...,\mathrm{9}\right\}\right) \\ $$$$\:^{\bullet} {first}\:{a}\:{can}\:{be}\:{filled}\:{in}\: \\ $$$$\:\:\:\left(\mathrm{U}−\left\{\mathrm{0}\right\}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{9}\:{ways} \\ $$$$\:^{\bullet} {first}\:{b}\:\left({from}\:{left}\right)\:{can}\:{be}\:{filled} \\ $$$$\:\:\:\:{in}\:\left(\mathrm{U}−\left\{{a}\right\}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{9}\:{ways} \\ $$$$\:^{\bullet} {first}\:{c}\:\left({from}\:{left}\right)\:{can}\:{be}\:{filled} \\ $$$$\:\:\:\:{in}\:\left(\mathrm{U}−\left\{{a},{b}\right\}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{8}\:{ways} \\ $$$$\:^{\bullet} {each}\:{of}\:{other}\:{a}'{s},{b}'{s},{c}'{s}\:\:{can}\: \\ $$$$\:\:\:{be}\:{filled}\:{in}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:{way} \\ $$$${Total}\:{ways}\:{in}\:{each}\:{case}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{9}×\mathrm{9}×\mathrm{8}=\mathrm{648} \\ $$$${Total}\:{of}\:\mathrm{25}\:{cases}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{648}×\mathrm{25}=\mathrm{16200} \\ $$

Commented by mr W last updated on 04/Jul/20

thanks for solving sir!

$${thanks}\:{for}\:{solving}\:{sir}! \\ $$

Answered by mr W last updated on 28/Jun/20

i found following general method. let′s consider the general case: n−digit numbers with exactly m different digits (m≤10≤n). at first let′s treat digit 0 like the other digits, i.e. a number may also begin with 0. to select m digits from the 10 available digits (0,1,2,...,9) there are C_m ^(10) ways. let′s treat the n digit positions in a n−digit number as n boxes and we are going to fill these boxes with balls in m different colours and each box should obtain at least one ball. to do this there are m!{_m ^n } ways. {_m ^n } are the so−called stirling numbers of the second kind. {_m ^n } is the number of ways to partition a set of n objects into m non−empty subsets. for the m colours to represent the m different digits there are m! ways. therefore number of n−digit numbers which can be formed by exactly m different digits is C_m ^(10) m!{_m ^n }. but among these numbers there are some ones which begin with 0. we know there are the same many numbers begining with 0 as with 1 or with 2 etc. so the number of numbers which don′t begin with 0 is (9/(10))×C_m ^(10) m!{_m ^n }. this is the answer of our question. with n=5, m=3 we get (9/(10))×C_3 ^(10) ×3!×{_3 ^5 } =(9/(10))×120×6×25=16200

$${i}\:{found}\:{following}\:{general}\:{method}. \\ $$$${let}'{s}\:{consider}\:{the}\:{general}\:{case}: \\ $$$${n}−{digit}\:{numbers}\:{with}\:{exactly}\:{m} \\ $$$${different}\:{digits}\:\left({m}\leqslant\mathrm{10}\leqslant{n}\right). \\ $$$${at}\:{first}\:{let}'{s}\:{treat}\:{digit}\:\mathrm{0}\:{like}\:{the}\:{other} \\ $$$${digits},\:{i}.{e}.\:{a}\:{number}\:{may}\:{also}\:{begin} \\ $$$${with}\:\mathrm{0}. \\ $$$${to}\:{select}\:{m}\:{digits}\:{from}\:{the}\:\mathrm{10} \\ $$$${available}\:{digits}\:\left(\mathrm{0},\mathrm{1},\mathrm{2},...,\mathrm{9}\right)\:{there}\:{are} \\ $$$${C}_{{m}} ^{\mathrm{10}} \:{ways}. \\ $$$${let}'{s}\:{treat}\:{the}\:{n}\:{digit}\:{positions}\:{in}\:{a} \\ $$$${n}−{digit}\:{number}\:{as}\:{n}\:{boxes}\:{and}\:{we} \\ $$$${are}\:{going}\:{to}\:{fill}\:{these}\:{boxes}\:{with}\:{balls} \\ $$$${in}\:{m}\:{different}\:{colours}\:{and}\:{each}\:{box} \\ $$$${should}\:{obtain}\:{at}\:{least}\:{one}\:{ball}.\:{to}\:{do} \\ $$$${this}\:{there}\:{are}\:{m}!\left\{_{{m}} ^{{n}} \right\}\:{ways}.\:\left\{_{{m}} ^{{n}} \right\}\:{are}\:{the} \\ $$$${so}−{called}\:{stirling}\:{numbers}\:{of}\:{the} \\ $$$${second}\:{kind}.\:\left\{_{{m}} ^{{n}} \right\}\:{is}\:{the}\:{number}\:{of}\:{ways} \\ $$$${to}\:{partition}\:{a}\:{set}\:{of}\:{n}\:{objects}\:{into}\:{m} \\ $$$${non}−{empty}\:{subsets}.\:{for}\:\:{the}\:{m} \\ $$$${colours}\:{to}\:{represent}\:{the}\:{m}\:{different} \\ $$$${digits}\:{there}\:{are}\:{m}!\:{ways}.\:{therefore} \\ $$$${number}\:{of}\:{n}−{digit}\:{numbers}\:{which} \\ $$$${can}\:{be}\:{formed}\:{by}\:{exactly}\:{m}\:{different} \\ $$$${digits}\:{is}\:{C}_{{m}} ^{\mathrm{10}} {m}!\left\{_{{m}} ^{{n}} \right\}.\:{but}\:{among}\:{these} \\ $$$${numbers}\:{there}\:{are}\:{some}\:{ones}\:{which} \\ $$$${begin}\:{with}\:\mathrm{0}.\:\:{we}\:{know}\:{there}\:{are}\:{the} \\ $$$${same}\:{many}\:{numbers}\:{begining}\:{with}\:\mathrm{0} \\ $$$${as}\:{with}\:\mathrm{1}\:{or}\:{with}\:\mathrm{2}\:{etc}.\:{so}\:{the}\:{number} \\ $$$${of}\:{numbers}\:{which}\:{don}'{t}\:{begin}\:{with}\:\mathrm{0} \\ $$$${is}\:\frac{\mathrm{9}}{\mathrm{10}}×{C}_{{m}} ^{\mathrm{10}} {m}!\left\{_{{m}} ^{{n}} \right\}.\:{this}\:{is}\:{the}\:{answer} \\ $$$${of}\:{our}\:{question}. \\ $$$${with}\:{n}=\mathrm{5},\:{m}=\mathrm{3}\:{we}\:{get} \\ $$$$\frac{\mathrm{9}}{\mathrm{10}}×{C}_{\mathrm{3}} ^{\mathrm{10}} ×\mathrm{3}!×\left\{_{\mathrm{3}} ^{\mathrm{5}} \right\} \\ $$$$=\frac{\mathrm{9}}{\mathrm{10}}×\mathrm{120}×\mathrm{6}×\mathrm{25}=\mathrm{16200} \\ $$

Commented by mr W last updated on 28/Jun/20

Commented by mr W last updated on 28/Jun/20

Commented by Rasheed.Sindhi last updated on 28/Jun/20

Deep thinking & Nice research!

$${Deep}\:{thinking}\:\&\:{Nice}\:{research}! \\ $$

Answered by ajfour last updated on 29/Jun/20

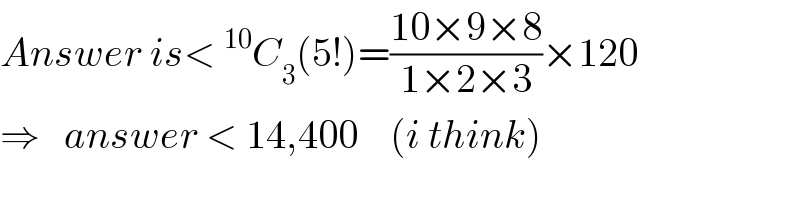
Answer is<^(10) C_3 (5!)=((10×9×8)/(1×2×3))×120 ⇒ answer < 14,400 (i think)

$${Answer}\:{is}<\:^{\mathrm{10}} {C}_{\mathrm{3}} \left(\mathrm{5}!\right)=\frac{\mathrm{10}×\mathrm{9}×\mathrm{8}}{\mathrm{1}×\mathrm{2}×\mathrm{3}}×\mathrm{120} \\ $$$$\Rightarrow\:\:\:{answer}\:<\:\mathrm{14},\mathrm{400}\:\:\:\:\left({i}\:{think}\right) \\ $$

Commented by mr W last updated on 29/Jun/20

this is not correct sir. with 5 different digits you can form 12345 ⇒5!=120 numvers. but with three different digits 1,2,3 you can form more 5 digit numbers: 11123: ⇒((5!)/(3!)) 12223: ⇒((5!)/(3!)) 12333: ⇒((5!)/(3!)) 11223: ⇒((5!)/(2!2!)) 11233: ⇒((5!)/(2!2!)) 12233: ⇒((5!)/(2!2!)) ⇒3×((5!)/(3!))+3×((5!)/(2!2!))=150 [=3!{_3 ^5 }=6×25] > 120

$${this}\:{is}\:{not}\:{correct}\:{sir}. \\ $$$${with}\:\mathrm{5}\:{different}\:{digits}\:{you}\:{can}\:{form} \\ $$$$\mathrm{12345}\:\Rightarrow\mathrm{5}!=\mathrm{120}\:{numvers}. \\ $$$$ \\ $$$${but}\:{with}\:{three}\:{different}\:{digits}\:\mathrm{1},\mathrm{2},\mathrm{3} \\ $$$${you}\:{can}\:{form}\:{more}\:\mathrm{5}\:{digit}\:{numbers}: \\ $$$$\mathrm{11123}:\:\Rightarrow\frac{\mathrm{5}!}{\mathrm{3}!} \\ $$$$\mathrm{12223}:\:\Rightarrow\frac{\mathrm{5}!}{\mathrm{3}!} \\ $$$$\mathrm{12333}:\:\Rightarrow\frac{\mathrm{5}!}{\mathrm{3}!} \\ $$$$\mathrm{11223}:\:\Rightarrow\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{2}!} \\ $$$$\mathrm{11233}:\:\Rightarrow\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{2}!} \\ $$$$\mathrm{12233}:\:\Rightarrow\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{2}!} \\ $$$$\Rightarrow\mathrm{3}×\frac{\mathrm{5}!}{\mathrm{3}!}+\mathrm{3}×\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{2}!}=\mathrm{150}\:\left[=\mathrm{3}!\left\{_{\mathrm{3}} ^{\mathrm{5}} \right\}=\mathrm{6}×\mathrm{25}\right]\:>\:\mathrm{120} \\ $$

Commented by ajfour last updated on 02/Jul/20

thanks for the light sir, i shall try to arrive at the answer, my way too.

$${thanks}\:{for}\:{the}\:{light}\:{sir},\:{i}\:{shall}\:{try} \\ $$$${to}\:{arrive}\:{at}\:{the}\:{answer},\:{my}\:{way}\:{too}. \\ $$

Answered by mr W last updated on 04/Jul/20

Classical way i also used: to select 3 digits from 10 there are C_3 ^(10) =120 ways. to build a five digit number with 3 different digits, say 1,2,3, there are following cases: case 1: one digit triple, two digits once each: 11123,22213,33312 ⇒3×((5!)/(3!)) ways case 2: one digit once, two digits twice each: 12233,21133,31122 ⇒3×((5!)/(2!2!)) ways ⇒totally C_3 ^(10) ×3×(((5!)/(3!))+((5!)/(2!2!)))=18000 but this includes also those numbers beginning with 0. to build a number beginning with 0, case 1: 01222,02221 ⇒2×((4!)/(3!))×C_2 ^9 case 2: 01122 ⇒((4!)/(2!2!))×C_2 ^9 case 3: 00112,00122 ⇒2×((4!)/(2!))×C_2 ^9 case 4: 00012 ⇒((4!)/(2!))×C_2 ^9 ⇒totally (2×((4!)/(3!))+((4!)/(2!2!))+2×((4!)/(2!))+((4!)/(2!)))×C_2 ^9 =1800 ⇒total valid five−digit numbers: 18000−1800=16200

$${Classical}\:{way}\:{i}\:{also}\:{used}: \\ $$$${to}\:{select}\:\mathrm{3}\:{digits}\:{from}\:\mathrm{10}\:{there}\:{are} \\ $$$${C}_{\mathrm{3}} ^{\mathrm{10}} =\mathrm{120}\:{ways}. \\ $$$${to}\:{build}\:{a}\:{five}\:{digit}\:{number}\:{with}\:\mathrm{3} \\ $$$${different}\:{digits},\:{say}\:\mathrm{1},\mathrm{2},\mathrm{3},\:{there}\:{are} \\ $$$${following}\:{cases}: \\ $$$${case}\:\mathrm{1}:\:{one}\:{digit}\:{triple},\:{two}\:{digits}\: \\ $$$${once}\:{each}: \\ $$$$\mathrm{11123},\mathrm{22213},\mathrm{33312}\:\Rightarrow\mathrm{3}×\frac{\mathrm{5}!}{\mathrm{3}!}\:{ways} \\ $$$${case}\:\mathrm{2}:\:{one}\:{digit}\:{once},\:{two}\:{digits}\: \\ $$$${twice}\:{each}: \\ $$$$\mathrm{12233},\mathrm{21133},\mathrm{31122}\:\Rightarrow\mathrm{3}×\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{2}!}\:{ways} \\ $$$$\Rightarrow{totally}\:{C}_{\mathrm{3}} ^{\mathrm{10}} ×\mathrm{3}×\left(\frac{\mathrm{5}!}{\mathrm{3}!}+\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{2}!}\right)=\mathrm{18000} \\ $$$${but}\:{this}\:{includes}\:{also}\:{those}\:{numbers} \\ $$$${beginning}\:{with}\:\mathrm{0}. \\ $$$${to}\:{build}\:{a}\:{number}\:{beginning}\:{with}\:\mathrm{0}, \\ $$$${case}\:\mathrm{1}:\:\mathrm{01222},\mathrm{02221}\:\Rightarrow\mathrm{2}×\frac{\mathrm{4}!}{\mathrm{3}!}×{C}_{\mathrm{2}} ^{\mathrm{9}} \\ $$$${case}\:\mathrm{2}:\:\mathrm{01122}\:\Rightarrow\frac{\mathrm{4}!}{\mathrm{2}!\mathrm{2}!}×{C}_{\mathrm{2}} ^{\mathrm{9}} \\ $$$${case}\:\mathrm{3}:\:\mathrm{00112},\mathrm{00122}\:\Rightarrow\mathrm{2}×\frac{\mathrm{4}!}{\mathrm{2}!}×{C}_{\mathrm{2}} ^{\mathrm{9}} \\ $$$${case}\:\mathrm{4}:\:\mathrm{00012}\:\Rightarrow\frac{\mathrm{4}!}{\mathrm{2}!}×{C}_{\mathrm{2}} ^{\mathrm{9}} \\ $$$$\Rightarrow{totally}\:\left(\mathrm{2}×\frac{\mathrm{4}!}{\mathrm{3}!}+\frac{\mathrm{4}!}{\mathrm{2}!\mathrm{2}!}+\mathrm{2}×\frac{\mathrm{4}!}{\mathrm{2}!}+\frac{\mathrm{4}!}{\mathrm{2}!}\right)×{C}_{\mathrm{2}} ^{\mathrm{9}} =\mathrm{1800} \\ $$$$ \\ $$$$\Rightarrow{total}\:{valid}\:{five}−{digit}\:{numbers}: \\ $$$$\mathrm{18000}−\mathrm{1800}=\mathrm{16200} \\ $$

Commented by Rasheed.Sindhi last updated on 04/Jul/20

Nice approach:Easy to understand!

$$\mathcal{N}{ice}\:{approach}:\mathcal{E}{asy}\:{to}\:{understand}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com