Math Question and Answers


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 100575 by bshahid010@gmail.com last updated on 27/Jun/20

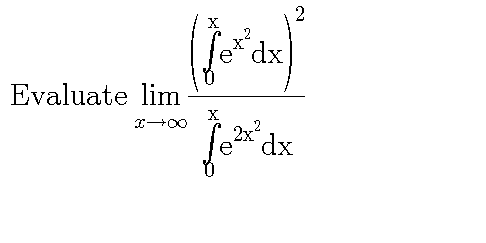
	Answered by Ar Brandon last updated on 27/Jun/20
	$Let I=lim_(x→∞) ∫_0 ^x e^x^2 dx=∫_0 ^∞ e^x^2 dx ⇒I= { ((∫_0 ^∞ e^x^2 dx)),((∫_0 ^∞ e^y^2 dy)) :} ⇒I^2 =∫_0 ^∞ ∫_0 ^∞ e^(x^2 +y^2 ) dxdy ⇒I^2 =∫_0 ^(π/2) ∫_0 ^∞ re^r^2 drdθ=[(θ/2)]_0 ^(π/2) [(e^r^2 /1)]_0 ^∞ =lim_(r→∞) (π/4)(e^r^2 −1) Let J=lim_(x→∞) ∫_0 ^x e^(2x^2 ) dx ⇒J= { ((∫_0 ^∞ e^(2x^2 ) dx)),((∫_0 ^∞ e^(2y^2 ) dy)) :} ⇒J^2 =∫_0 ^∞ ∫_0 ^∞ e^(2(x^2 +y^2 )) dxdy ⇒J^2 =∫_0 ^(π/2) ∫_0 ^∞ re^(2r^2 ) drdθ=[(θ/4)]_0 ^(π/2) [(e^(2r^2 ) /1)]_0 ^∞ =lim_(r→∞) (π/8)(e^(2r^2 ) −1) ⇒lim_(x→∞) (((∫_0 ^x e^x^2 dx)^2 )/(∫_0 ^x e^(2x^2 ) ))=lim_(r→∞) (((π/4)(e^r^2 −1))/(√((π/8)(e^(2r^2 ) −1))))=lim_(r→∞) ((π(1−(1/e^r^2 )))/(√(2π(1−(1/e^(2r^2 ) ))))) =(π/(√(2π)))=(√(π/2))$
	$Let I = \lim_{x \to \infty} \int_{0}^{x} e^{x^{2}} dx = \int_{0}^{\infty} e^{x^{2}} dx$ $\Rightarrow I = {\begin{cases} \int_{0}^{\infty} e^{x^{2}} dx \\ \int_{0}^{\infty} e^{y^{2}} dy \end{cases} \Rightarrow I^{2} = \int_{0}^{\infty} \int_{0}^{\infty} e^{x^{2} + y^{2}} dxdy$ $\Rightarrow I^{2} = \int_{0}^{\frac{π}{2}} \int_{0}^{\infty} {re}^{r^{2}} drd θ = {[\frac{θ}{2}]}_{0}^{\frac{π}{2}} {[\frac{e^{r^{2}}}{1}]}_{0}^{\infty} = \lim_{r \to \infty} \frac{π}{4} (e^{r^{2}} - 1)$ $Let J = \lim_{x \to \infty} \int_{0}^{x} e^{{2 x}^{2}} dx$ $\Rightarrow J = {\begin{cases} \int_{0}^{\infty} e^{{2 x}^{2}} dx \\ \int_{0}^{\infty} e^{{2 y}^{2}} dy \end{cases} \Rightarrow J^{2} = \int_{0}^{\infty} \int_{0}^{\infty} e^{2 (x^{2} + y^{2})} dxdy$ $\Rightarrow J^{2} = \int_{0}^{\frac{π}{2}} \int_{0}^{\infty} {re}^{{2 r}^{2}} drd θ = {[\frac{θ}{4}]}_{0}^{\frac{π}{2}} {[\frac{e^{{2 r}^{2}}}{1}]}_{0}^{\infty} = \lim_{r \to \infty} \frac{π}{8} (e^{{2 r}^{2}} - 1)$ $\Rightarrow \lim_{x \to \infty} \frac{{(\int_{0}^{x} e^{x^{2}} dx)}^{2}}{\int_{0}^{x} e^{{2 x}^{2}}} = \lim_{r \to \infty} \frac{\frac{π}{4} (e^{r^{2}} - 1)}{\sqrt{\frac{π}{8} (e^{{2 r}^{2}} - 1)}} = \lim_{r \to \infty} \frac{π (1 - \frac{1}{e^{r^{2}}})}{\sqrt{2 π (1 - \frac{1}{e^{{2 r}^{2}}})}}$ $= \frac{π}{\sqrt{2 π}} = \sqrt{\frac{π}{2}}$
	Commented by Coronavirus last updated on 27/Jun/20

	$C l e a n$
	Commented by Ar Brandon last updated on 27/Jun/20
	Ouais Corona, sdk ? C'est Einstein. Avec ton nom bizarre là.��
	Commented by Coronavirus last updated on 27/Jun/20
	ça va je profite du savoir de ce forum
	Commented by Ar Brandon last updated on 27/Jun/20
	Super ��
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum