
Question Number 100624 by Dwaipayan Shikari last updated on 27/Jun/20
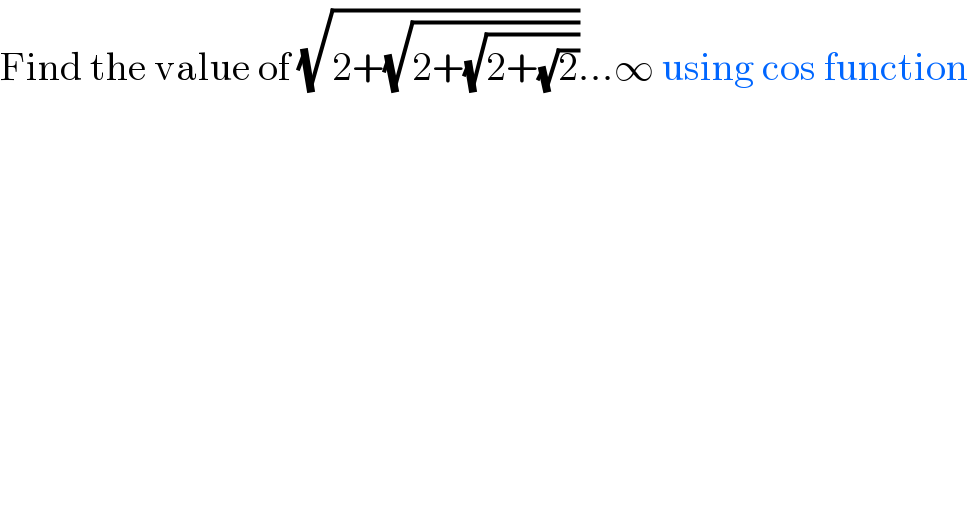
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}}...\infty\:\mathrm{using}\:\mathrm{cos}\:\mathrm{function} \\ $$
Commented by MJS last updated on 27/Jun/20

$$\mathrm{why}\:\mathrm{cos}? \\ $$$${x}=\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}....}}}} \\ $$$${x}^{\mathrm{2}} =\mathrm{2}{x} \\ $$$${x}_{\mathrm{1}} =\mathrm{0}\:\mathrm{wrong} \\ $$$${x}_{\mathrm{2}} =\mathrm{2}\:\mathrm{is}\:\mathrm{the}\:\mathrm{solution} \\ $$
Commented by Dwaipayan Shikari last updated on 27/Jun/20

$${There}\:{was}\:{a}\:{mistake}\:{on}\:{my}\:{question}.\:{Now}\:{can}\:{you}\:{prove}\:{it} \\ $$$${sir}\:{using}\:\boldsymbol{{cos}}\:\boldsymbol{{function}}????\:\:\boldsymbol{{I}}\:\boldsymbol{{have}}\:\boldsymbol{{edited}}\:\boldsymbol{{my}}\:\boldsymbol{{question}} \\ $$
Commented by Dwaipayan Shikari last updated on 27/Jun/20
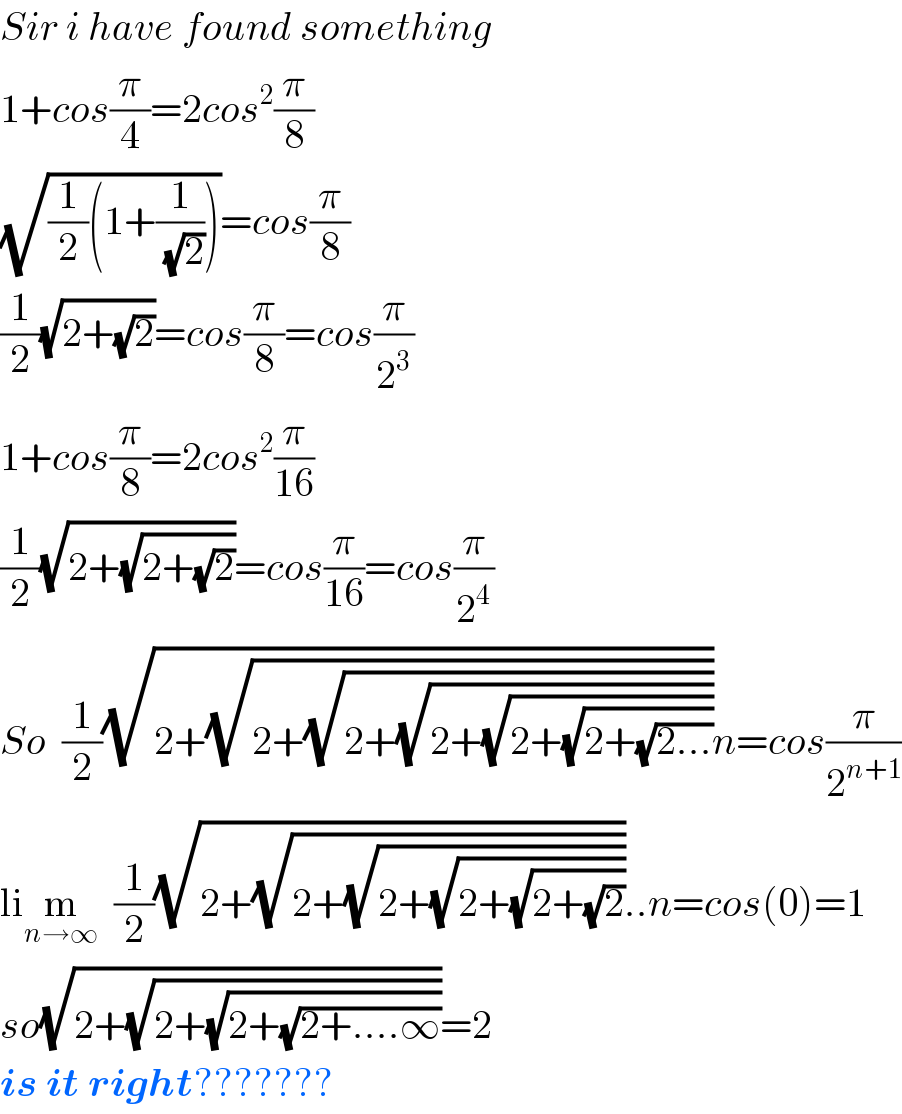
$${Sir}\:{i}\:{have}\:{found}\:{something} \\ $$$$\mathrm{1}+{cos}\frac{\pi}{\mathrm{4}}=\mathrm{2}{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{8}} \\ $$$$\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)}={cos}\frac{\pi}{\mathrm{8}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}={cos}\frac{\pi}{\mathrm{8}}={cos}\frac{\pi}{\mathrm{2}^{\mathrm{3}} } \\ $$$$\mathrm{1}+{cos}\frac{\pi}{\mathrm{8}}=\mathrm{2}{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{16}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}={cos}\frac{\pi}{\mathrm{16}}={cos}\frac{\pi}{\mathrm{2}^{\mathrm{4}} } \\ $$$${So}\:\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}...}}}}}}}{n}={cos}\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$$\mathrm{li}\underset{{n}\rightarrow\infty} {\mathrm{m}}\:\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}}}}..{n}={cos}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${so}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+....\infty}}}}=\mathrm{2} \\ $$$$\boldsymbol{{is}}\:\boldsymbol{{it}}\:\boldsymbol{{right}}??????? \\ $$
Answered by maths mind last updated on 27/Jun/20
![u_(n+1) ^2 =u_n +2...E u_0 =(√2) we can proof this withe logic 0≤u_n ≤2...easy too see u_(n+1) −u_n =((u_n +2−u_n ^2 )/((√(u_n +2))+u_n ))=((−(u_n −2)(u_n +1))/((√(u_n +2))+u_n ))≥0 u_n ↾ increasing ⇒ since0 ≤U_n ≤2 ⇒∃ (w_n ) such u_n =2cos(w_n ) proof w_n =cos^(−1) ((u_n /2)) well defind since (u_n /2)∈[0,1] since u_n ∈[0,2] and incrasing ⇒w_n ∈[0,(π/2)]⇒ w_n is deacrising E⇔4cos^2 (w_(n+1) )=2+2cos(w_n )⇒2cos^2 (w_(n+1) )−1=cos(w_n ) cos(2x)=2cos^2 (x)−1⇒ E⇔cos(2w_(n+1) )=cos(w_n ) ⇒2w_(n+1) =w_n because w_n ∈[0,(π/2)] ⇒w_(n+1) =(w_n /2)⇒w_n is geometric sequences ⇒w_n =w_0 ((1/2))^n w_0 =(π/4) u_n =2cos((π/(4.2^n )))=2cos((π/2^(n+2) ))](Q100635.png)
$${u}_{{n}+\mathrm{1}} ^{\mathrm{2}} ={u}_{{n}} +\mathrm{2}...{E} \\ $$$${u}_{\mathrm{0}} =\sqrt{\mathrm{2}} \\ $$$${we}\:{can}\:{proof}\:{this}\:\:{withe}\:\:{logic} \\ $$$$\mathrm{0}\leqslant{u}_{{n}} \leqslant\mathrm{2}...{easy}\:{too}\:{see} \\ $$$${u}_{{n}+\mathrm{1}} −{u}_{{n}} =\frac{{u}_{{n}} +\mathrm{2}−{u}_{{n}} ^{\mathrm{2}} }{\sqrt{{u}_{{n}} +\mathrm{2}}+{u}_{{n}} }=\frac{−\left({u}_{{n}} −\mathrm{2}\right)\left({u}_{{n}} +\mathrm{1}\right)}{\sqrt{{u}_{{n}} +\mathrm{2}}+{u}_{{n}} }\geqslant\mathrm{0} \\ $$$${u}_{{n}} \upharpoonright\:{increasing}\: \\ $$$$\Rightarrow\:\:{since}\mathrm{0}\:\leqslant{U}_{{n}} \leqslant\mathrm{2} \\ $$$$\Rightarrow\exists\:\left({w}_{{n}} \right)\:{such}\:{u}_{{n}} =\mathrm{2}{cos}\left({w}_{{n}} \right)\:{proof} \\ $$$${w}_{{n}} =\mathrm{cos}^{−\mathrm{1}} \left(\frac{{u}_{{n}} }{\mathrm{2}}\right)\:{well}\:{defind}\:{since}\:\frac{{u}_{{n}} }{\mathrm{2}}\in\left[\mathrm{0},\mathrm{1}\right] \\ $$$${since}\:{u}_{{n}} \in\left[\mathrm{0},\mathrm{2}\right]\:{and}\:{incrasing}\:\Rightarrow{w}_{{n}} \in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right]\Rightarrow \\ $$$${w}_{{n}} \:{is}\:{deacrising} \\ $$$${E}\Leftrightarrow\mathrm{4}{cos}^{\mathrm{2}} \left({w}_{{n}+\mathrm{1}} \right)=\mathrm{2}+\mathrm{2}{cos}\left({w}_{{n}} \right)\Rightarrow\mathrm{2}{cos}^{\mathrm{2}} \left({w}_{{n}+\mathrm{1}} \right)−\mathrm{1}={cos}\left({w}_{{n}} \right) \\ $$$${cos}\left(\mathrm{2}{x}\right)=\mathrm{2}{cos}^{\mathrm{2}} \left({x}\right)−\mathrm{1}\Rightarrow \\ $$$${E}\Leftrightarrow{cos}\left(\mathrm{2}{w}_{{n}+\mathrm{1}} \right)={cos}\left({w}_{{n}} \right) \\ $$$$\Rightarrow\mathrm{2}{w}_{{n}+\mathrm{1}} ={w}_{{n}} \:{because}\:{w}_{{n}} \in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right] \\ $$$$\Rightarrow{w}_{{n}+\mathrm{1}} =\frac{{w}_{{n}} }{\mathrm{2}}\Rightarrow{w}_{{n}} {is}\:{geometric}\:{sequences} \\ $$$$\Rightarrow{w}_{{n}} ={w}_{\mathrm{0}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \:\:{w}_{\mathrm{0}} =\frac{\pi}{\mathrm{4}} \\ $$$${u}_{{n}} =\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{4}.\mathrm{2}^{{n}} }\right)=\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{2}^{{n}+\mathrm{2}} }\right) \\ $$$$ \\ $$
Commented by ghiniboss last updated on 28/Jun/20
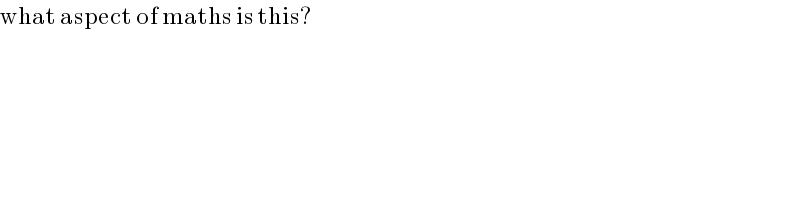
$$\mathrm{what}\:\mathrm{aspect}\:\mathrm{of}\:\mathrm{maths}\:\mathrm{is}\:\mathrm{this}? \\ $$
Commented by prakash jain last updated on 28/Jun/20

$$\mathrm{Two}\:\mathrm{topics} \\ $$$$\mathrm{Sequences}\:\mathrm{and}\:\mathrm{series} \\ $$$$\mathrm{recurrence}\:\mathrm{relation} \\ $$
