Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 100966 by mhmd last updated on 29/Jun/20

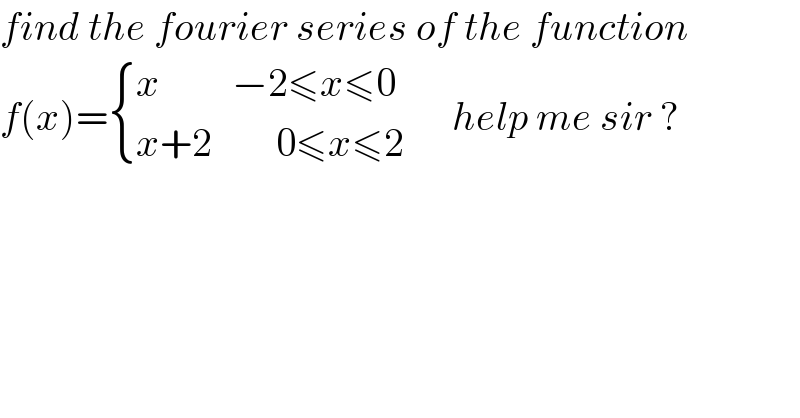
find the fourier series of the function f(x)= { ((x −2≤x≤0)),((x+2 0≤x≤2)) :} help me sir ?

$${find}\:{the}\:{fourier}\:{series}\:{of}\:{the}\:{function} \\ $$$${f}\left({x}\right)=\begin{cases}{{x}\:\:\:\:\:\:\:\:\:−\mathrm{2}\leqslant{x}\leqslant\mathrm{0}}\\{{x}+\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{0}\leqslant{x}\leqslant\mathrm{2}}\end{cases}\:\:\:\:\:\:{help}\:{me}\:{sir}\:? \\ $$

Commented by bobhans last updated on 29/Jun/20

f(x) = (a_o /2) + Σ_(n=1) ^∞ b_n cos (((nπx)/L)) b_n =(2/4) [ ∫_(−2) ^0 x sin (((nπx)/4)) dx + ∫_0 ^2 (x+2)sin (((nπx)/4)) dx ] b_n = (1/2)[ ∫_(−2) ^2 x sin (((nπx)/4)) dx + ∫_0 ^2 2 sin (((nπx)/4)) dx ] b_n = (1/2)[ −((4x)/(nπ)) cos (((nπx)/4))+((16)/((nπ)^2 )) sin (((nπx)/4)) ]_(−2) ^2 − (1/2) [ (8/(nπ)) cos (((nπx)/4)) ]_0 ^2

$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{a}_{\mathrm{o}} }{\mathrm{2}}\:+\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\mathrm{b}_{\mathrm{n}} \mathrm{cos}\:\left(\frac{\mathrm{n}\pi\mathrm{x}}{\mathrm{L}}\right) \\ $$$$\mathrm{b}_{\mathrm{n}} =\frac{\mathrm{2}}{\mathrm{4}}\:\left[\:\underset{−\mathrm{2}} {\overset{\mathrm{0}} {\int}}\mathrm{x}\:\mathrm{sin}\:\left(\frac{\mathrm{n}\pi\mathrm{x}}{\mathrm{4}}\right)\:\mathrm{dx}\:+\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\left(\mathrm{x}+\mathrm{2}\right)\mathrm{sin}\:\left(\frac{\mathrm{n}\pi\mathrm{x}}{\mathrm{4}}\right)\:\mathrm{dx}\:\right] \\ $$$$\mathrm{b}_{\mathrm{n}} =\:\frac{\mathrm{1}}{\mathrm{2}}\left[\:\underset{−\mathrm{2}} {\overset{\mathrm{2}} {\int}}\mathrm{x}\:\mathrm{sin}\:\left(\frac{\mathrm{n}\pi\mathrm{x}}{\mathrm{4}}\right)\:\mathrm{dx}\:+\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\mathrm{2}\:\mathrm{sin}\:\left(\frac{\mathrm{n}\pi\mathrm{x}}{\mathrm{4}}\right)\:\mathrm{dx}\:\right] \\ $$$$\mathrm{b}_{\mathrm{n}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\:−\frac{\mathrm{4x}}{\mathrm{n}\pi}\:\mathrm{cos}\:\left(\frac{\mathrm{n}\pi\mathrm{x}}{\mathrm{4}}\right)+\frac{\mathrm{16}}{\left(\mathrm{n}\pi\right)^{\mathrm{2}} }\:\mathrm{sin}\:\left(\frac{\mathrm{n}\pi\mathrm{x}}{\mathrm{4}}\right)\:\right]_{−\mathrm{2}} ^{\mathrm{2}} \\ $$$$−\:\frac{\mathrm{1}}{\mathrm{2}}\:\left[\:\frac{\mathrm{8}}{\mathrm{n}\pi}\:\mathrm{cos}\:\left(\frac{\mathrm{n}\pi\mathrm{x}}{\mathrm{4}}\right)\:\right]_{\mathrm{0}} ^{\mathrm{2}} \: \\ $$$$ \\ $$

Commented by mhmd last updated on 29/Jun/20

how are you sir ? am dont anderstand how [bn cos(((nπx)/L))] because the fourier series is given by f(x)=((ao)/2)+some (n≥1)[an cos(((nπx)/L))+bn sin(((nπx)/l))] how bn cos(((nπx)/L)) and where an cos(((nπx)/L)) blease sir can you exact this blease im very want this equestion ?

$${how}\:{are}\:{you}\:{sir}\:?\:{am}\:{dont}\:{anderstand}\:{how}\:\left[{bn}\:{cos}\left(\frac{{n}\pi{x}}{{L}}\right)\right]\: \\ $$$${because}\:{the}\:{fourier}\:{series}\:{is}\:{given}\:{by}\: \\ $$$${f}\left({x}\right)=\frac{{ao}}{\mathrm{2}}+{some}\:\left({n}\geqslant\mathrm{1}\right)\left[{an}\:{cos}\left(\frac{{n}\pi{x}}{{L}}\right)+{bn}\:{sin}\left(\frac{{n}\pi{x}}{{l}}\right)\right] \\ $$$${how}\:{bn}\:{cos}\left(\frac{{n}\pi{x}}{{L}}\right)\:{and}\:{where}\:{an}\:{cos}\left(\frac{{n}\pi{x}}{{L}}\right)\:{blease}\:{sir}\:{can}\:{you}\:{exact}\:{this}\:{blease} \\ $$$${im}\:{very}\:{want}\:{this}\:{equestion}\:? \\ $$

Commented by mathmax by abdo last updated on 29/Jun/20

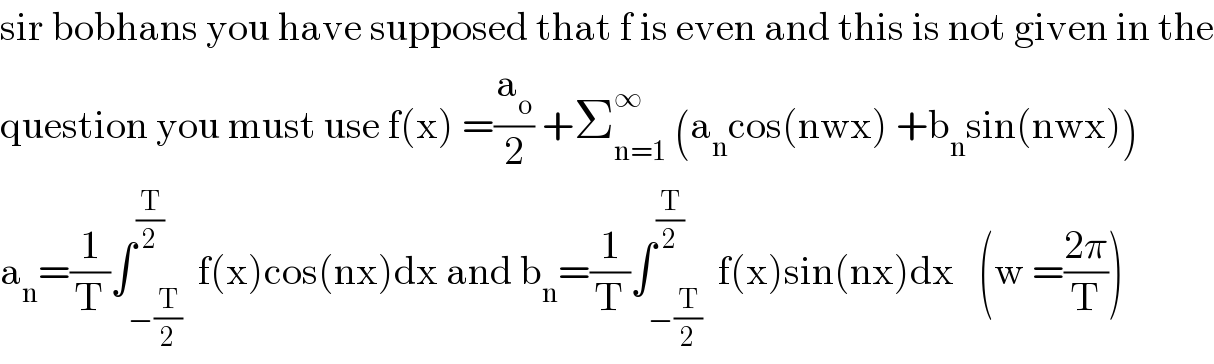
sir bobhans you have supposed that f is even and this is not given in the question you must use f(x) =(a_o /2) +Σ_(n=1) ^∞ (a_n cos(nwx) +b_n sin(nwx)) a_n =(1/T)∫_(−(T/2)) ^(T/2) f(x)cos(nx)dx and b_n =(1/T)∫_(−(T/2)) ^(T/2) f(x)sin(nx)dx (w =((2π)/T))

$$\mathrm{sir}\:\mathrm{bobhans}\:\mathrm{you}\:\mathrm{have}\:\mathrm{supposed}\:\mathrm{that}\:\mathrm{f}\:\mathrm{is}\:\mathrm{even}\:\mathrm{and}\:\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{given}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{question}\:\mathrm{you}\:\mathrm{must}\:\mathrm{use}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{a}_{\mathrm{o}} }{\mathrm{2}}\:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left(\mathrm{a}_{\mathrm{n}} \mathrm{cos}\left(\mathrm{nwx}\right)\:+\mathrm{b}_{\mathrm{n}} \mathrm{sin}\left(\mathrm{nwx}\right)\right) \\ $$$$\mathrm{a}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{T}}\int_{−\frac{\mathrm{T}}{\mathrm{2}}} ^{\frac{\mathrm{T}}{\mathrm{2}}} \:\mathrm{f}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{nx}\right)\mathrm{dx}\:\mathrm{and}\:\mathrm{b}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{T}}\int_{−\frac{\mathrm{T}}{\mathrm{2}}} ^{\frac{\mathrm{T}}{\mathrm{2}}} \:\mathrm{f}\left(\mathrm{x}\right)\mathrm{sin}\left(\mathrm{nx}\right)\mathrm{dx}\:\:\:\left(\mathrm{w}\:=\frac{\mathrm{2}\pi}{\mathrm{T}}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com