
Question Number 101220 by Ar Brandon last updated on 01/Jul/20
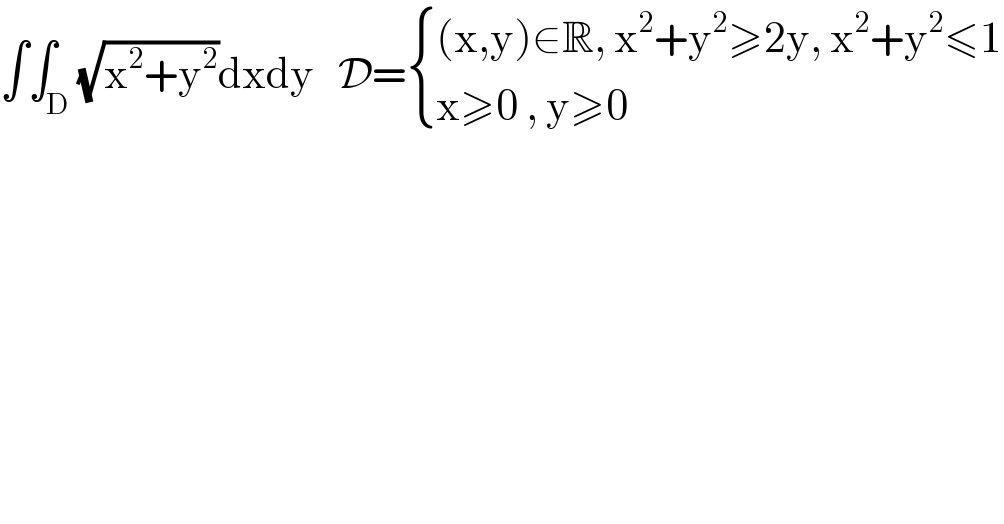
$$\int\int_{\mathrm{D}} \sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\mathrm{dxdy}\:\:\:\mathcal{D}=\begin{cases}{\left(\mathrm{x},\mathrm{y}\right)\in\mathbb{R},\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \geqslant\mathrm{2y},\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \leqslant\mathrm{1}}\\{\mathrm{x}\geqslant\mathrm{0}\:,\:\mathrm{y}\geqslant\mathrm{0}}\end{cases} \\ $$
Answered by Ar Brandon last updated on 03/Jul/20
![I=∫∫_D (√(x^2 +y^2 ))dxdy , D= { (((x,y) ∈R, x^2 +y^2 ≥2y, x^2 +y^2 ≤1)),((x≥0 , y≥0)) :} {: (),() } En coordonne^� es polaires; { ((x=rcosθ)),((y=rsinθ)) :} ⇒ { ((r^2 ≥2rsinθ)),((r^2 ≤1)) :} ⇒2sinθ≤r≤1 x^2 +y^2 ≥2y ⇒ r^2 ≥2rsinθ ⇒(1/2)≥sinθ ⇒ (π/6)≥θ≥0 ⇒I=∫_0 ^(π/6) ∫_(2sinθ) ^1 r^2 drdθ=∫_0 ^(π/6) [(r^3 /3)]_(2sinθ) ^1 dθ=∫_0 ^(π/6) [(1/3)−((8sin^3 θ)/3)]dθ ⇒3I=∫_0 ^(π/6) (1−8sin^3 θ)dθ=[θ]_0 ^(π/6) −8∫_0 ^(π/6) (1−cos^2 θ)sinθdθ =(π/6)+8[cosθ−((cos^3 θ)/3)]_0 ^(π/6) =(π/6)+8[((√3)/2)−((√3)/8)−1+(1/3)] =(π/6)+8(((3(√3))/8)−(2/3))=(π/6)+3(√3)−((16)/3) ⇒I=(π/(18))+(√3)−((16)/9)](Q101357.png)
$$ \\ $$$$ \\ $$$$\:\mathcal{I}=\int\int_{\mathcal{D}} \sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\mathrm{dxdy}\:,\:\mathcal{D}=\begin{cases}{\left(\mathrm{x},\mathrm{y}\right)\:\in\mathbb{R},\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \geqslant\mathrm{2y},\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \leqslant\mathrm{1}}\\{\mathrm{x}\geqslant\mathrm{0}\:,\:\mathrm{y}\geqslant\mathrm{0}}\end{cases}\left.\begin{matrix}{}\\{}\end{matrix}\right\} \\ $$$$\mathrm{En}\:\mathrm{coordonn}\acute {\mathrm{e}es}\:\mathrm{polaires}; \\ $$$$\begin{cases}{\mathrm{x}=\mathrm{rcos}\theta}\\{\mathrm{y}=\mathrm{rsin}\theta}\end{cases}\:\:\Rightarrow\:\:\begin{cases}{\mathrm{r}^{\mathrm{2}} \geqslant\mathrm{2rsin}\theta}\\{\mathrm{r}^{\mathrm{2}} \leqslant\mathrm{1}}\end{cases}\:\:\Rightarrow\mathrm{2sin}\theta\leqslant\mathrm{r}\leqslant\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \geqslant\mathrm{2y}\:\Rightarrow\:\mathrm{r}^{\mathrm{2}} \geqslant\mathrm{2rsin}\theta\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\geqslant\mathrm{sin}\theta\:\Rightarrow\:\frac{\pi}{\mathrm{6}}\geqslant\theta\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \int_{\mathrm{2sin}\theta} ^{\mathrm{1}} \mathrm{r}^{\mathrm{2}} \mathrm{drd}\theta=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \left[\frac{\mathrm{r}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{2sin}\theta} ^{\mathrm{1}} \mathrm{d}\theta=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \left[\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{8sin}^{\mathrm{3}} \theta}{\mathrm{3}}\right]\mathrm{d}\theta \\ $$$$\Rightarrow\mathrm{3}\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \left(\mathrm{1}−\mathrm{8sin}^{\mathrm{3}} \theta\right)\mathrm{d}\theta=\left[\theta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} −\mathrm{8}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \theta\right)\mathrm{sin}\theta\mathrm{d}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\pi}{\mathrm{6}}+\mathrm{8}\left[\mathrm{cos}\theta−\frac{\mathrm{cos}^{\mathrm{3}} \theta}{\mathrm{3}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} =\frac{\pi}{\mathrm{6}}+\mathrm{8}\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{8}}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\pi}{\mathrm{6}}+\mathrm{8}\left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}−\frac{\mathrm{2}}{\mathrm{3}}\right)=\frac{\pi}{\mathrm{6}}+\mathrm{3}\sqrt{\mathrm{3}}−\frac{\mathrm{16}}{\mathrm{3}} \\ $$$$\Rightarrow\mathcal{I}=\frac{\pi}{\mathrm{18}}+\sqrt{\mathrm{3}}−\frac{\mathrm{16}}{\mathrm{9}} \\ $$
