
Question Number 101375 by ajfour last updated on 02/Jul/20

Commented by ajfour last updated on 02/Jul/20

$${In}\:{terms}\:{of}\:{R},\:{find}\:{radii}\:{a},{b},{c}. \\ $$
Commented by ajfour last updated on 05/Jul/20

Commented by ajfour last updated on 06/Jul/20
![lets consider both circles of radii a and c generally. Both are at a distance of (R+r) from center M of circle of radius R. Both touch the line y=R^2 +(1/4)+R both touch the parabola at (x,x^2 ) x_1 =(√(R^2 −(1/4))) center of our general circle is (2(√(Rr)) , R^2 +(1/4)+R−r) eq. of the circle: { (((x−2(√(Rr)))^2 +[x^2 −(R^2 +(1/4)+R−r)]^2 =r^2 )),(((R+(1/2))^2 −r−(r/(√(1+4x^2 ))) = x^2 )) :} and x−2(√(Rr)) = ((r(2x))/(√(1+4x^2 ))) for r=c but 2(√(Rr))−x=((r(2x))/(√(1+4x^2 ))) for r=a And since we know x_1 =(√(R^2 −(1/4))) 2(√(Rr_1 ))=x+((2x_1 r)/(√(1+4x_1 ^2 ))) 2(√(Ra))=(√(R^2 −(1/4))) + ((2a(√(R^2 −(1/4))))/(√(1+4R^2 −1))) 2(√(Ra))=(√(R^2 −(1/4))) + (a/R)(√(R^2 −(1/4))) (a/R)(√(R^2 −(1/4))) −2R(√(a/R)) +(√(R^2 −(1/4)))=0 (√(a/R))=(R/(√(R^2 −(1/4))))±(√((R^2 /(R^2 −(1/4)))−1)) (√(a/R)) =((R±(1/2))/(√(R^2 −(1/4)))) ⇒ (a/R)=(((R±(1/2))^2 )/((R+(1/2))(R−(1/2)))) It seems (a/R)=(((R+(1/2)))/((R−(1/2)))) example R=2 ⇒ a=((10)/3) ..........](Q101900.png)
$${lets}\:{consider}\:{both}\:{circles}\:{of}\:{radii} \\ $$$${a}\:{and}\:{c}\:{generally}. \\ $$$${Both}\:{are}\:{at}\:{a}\:{distance}\:{of}\:\left({R}+{r}\right)\:{from} \\ $$$${center}\:{M}\:{of}\:{circle}\:{of}\:{radius}\:{R}. \\ $$$${Both}\:{touch}\:{the}\:{line}\:{y}={R}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}+{R} \\ $$$${both}\:{touch}\:{the}\:{parabola}\:{at}\:\left({x},{x}^{\mathrm{2}} \right) \\ $$$${x}_{\mathrm{1}} =\sqrt{{R}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$${center}\:{of}\:{our}\:{general}\:{circle}\:{is} \\ $$$$\:\:\:\:\:\left(\mathrm{2}\sqrt{{Rr}}\:,\:{R}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}+{R}−{r}\right) \\ $$$${eq}.\:{of}\:{the}\:{circle}: \\ $$$$\begin{cases}{\left({x}−\mathrm{2}\sqrt{{Rr}}\right)^{\mathrm{2}} +\left[{x}^{\mathrm{2}} −\left({R}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}+{R}−{r}\right)\right]^{\mathrm{2}} ={r}^{\mathrm{2}} }\\{\left({R}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −{r}−\frac{{r}}{\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }}\:=\:{x}^{\mathrm{2}} }\end{cases} \\ $$$$\:\:\:\:{and}\:\:\:{x}−\mathrm{2}\sqrt{{Rr}}\:=\:\frac{{r}\left(\mathrm{2}{x}\right)}{\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }}\:\:\:{for}\:{r}={c} \\ $$$${but}\:\:\:\:\:\mathrm{2}\sqrt{{Rr}}−{x}=\frac{{r}\left(\mathrm{2}{x}\right)}{\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }}\:\:\:\:\:\:\:{for}\:{r}={a} \\ $$$${And}\:{since}\:{we}\:{know}\:{x}_{\mathrm{1}} =\sqrt{{R}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\:\:\:\:\:\mathrm{2}\sqrt{{Rr}_{\mathrm{1}} }={x}+\frac{\mathrm{2}{x}_{\mathrm{1}} {r}}{\sqrt{\mathrm{1}+\mathrm{4}{x}_{\mathrm{1}} ^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\mathrm{2}\sqrt{{Ra}}=\sqrt{{R}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}\:+\:\frac{\mathrm{2}{a}\sqrt{{R}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}}{\sqrt{\mathrm{1}+\mathrm{4}{R}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\mathrm{2}\sqrt{{Ra}}=\sqrt{{R}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}\:+\:\frac{{a}}{{R}}\sqrt{{R}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\frac{{a}}{{R}}\sqrt{{R}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}\:−\mathrm{2}{R}\sqrt{\frac{{a}}{{R}}}\:+\sqrt{{R}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}=\mathrm{0} \\ $$$$\sqrt{\frac{{a}}{{R}}}=\frac{{R}}{\sqrt{{R}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}}\pm\sqrt{\frac{{R}^{\mathrm{2}} }{{R}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\sqrt{\frac{{a}}{{R}}}\:=\frac{{R}\pm\frac{\mathrm{1}}{\mathrm{2}}}{\sqrt{{R}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}} \\ $$$$\Rightarrow\:\:\frac{{a}}{{R}}=\frac{\left({R}\pm\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{\left({R}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({R}−\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$${It}\:{seems}\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\frac{\boldsymbol{{a}}}{\boldsymbol{{R}}}=\frac{\left(\boldsymbol{{R}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\left(\boldsymbol{{R}}−\frac{\mathrm{1}}{\mathrm{2}}\right)}\:\:\:\:\: \\ $$$${example}\:\:\:{R}=\mathrm{2}\:\:\Rightarrow\:\:\:{a}=\frac{\mathrm{10}}{\mathrm{3}} \\ $$$$\:..........\:\:\:\:\:\: \\ $$
Commented by ajfour last updated on 05/Jul/20

Answered by mr W last updated on 05/Jul/20
![Center of circle with radius R is M(0,m) y=x^2 x^2 +(y−m)^2 =R^2 ⇒y+(y−m)^2 =R^2 ⇒y^2 −(2m−1)y+m^2 −R^2 =0 Δ=(2m−1)^2 −4(m^2 −R^2 )=0 1+4R^2 −4m=0 ⇒m=(1/4)+R^2 Center of circle with radius b is B(0,m+R+b) x^2 +(y−m−R−b)^2 =b^2 y+[y−((1/4)+R^2 +R+b)]^2 =b^2 y^2 −2(R^2 +R+b−(1/4))y+(R^2 +R+b+(1/4))^2 −b^2 =0 Δ=(R^2 +R+b−(1/4))^2 −(R^2 +R+b+(1/4))^2 +b^2 =0 b^2 −b−(R^2 +R)=0 ⇒b=(1/2)(1+2R+1)=R+1 Center of circle with radius a is A(2(√(Ra)),m+R−a) it touches the parabola at P(p, p^2 ). tan θ=2p=((2(√(Ra)))/(a−R)) ⇒p=((√(Ra))/(a−R)) (2(√(Ra))−p)^2 +(m+R−a−p^2 )^2 =a^2 (2(√(Ra))−((√(Ra))/(a−R)))^2 +[m+R−a−((Ra)/((a−R)^2 ))]^2 =a^2 [2−(1/(R((a/R)−1)))]^2 ((a/R))+(1/R^2 )[m−R((a/R)−1)−((a/R)/(((a/R)−1)^2 ))]^2 =((a/R))^2 [2−(1/(R(ξ−1)))]^2 ξ+(1/R^2 )[(1/4)+R^2 −R(ξ−1)−(ξ/((ξ−1)^2 ))]^2 =ξ^2 ⇒ξ=... Center of circle with radius c is C(2(√(Rc)),m+R−c) it touches the parabola at Q(q, q^2 ). tan ϕ=2q q=2(√(Rc))+c sin ϕ=2(√(Rc))+((2cq)/(√(1+4q^2 ))) ⇒q−2(√(Rc))=((2cq)/(√(1+4q^2 ))) ...(i) q^2 =m+R−c−c cos ϕ=m+R−c−(c/(√(1+4q^2 ))) ⇒m+R−c−q^2 =(c/(√(1+4q^2 ))) ...(ii) q−2(√(Rc))=2q(m+R−c−q^2 ) q^3 −(R^2 +R−c−(1/4))q−(√(Rc))=0 ⇒q=((((√(Rc))/2)+(√(((Rc)/4)−(((R^2 +R−c−(1/4))^3 )/(27))))))^(1/3) +((((√(Rc))/2)−(√(((Rc)/4)−(((R^2 +R−c−(1/4))^3 )/(27))))))^(1/3) put this into (i) or (ii) to get c](Q101401.png)
$${Center}\:{of}\:{circle}\:{with}\:{radius}\:{R}\:{is} \\ $$$${M}\left(\mathrm{0},{m}\right) \\ $$$${y}={x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\left({y}−{m}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\Rightarrow{y}+\left({y}−{m}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\Rightarrow{y}^{\mathrm{2}} −\left(\mathrm{2}{m}−\mathrm{1}\right){y}+{m}^{\mathrm{2}} −{R}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Delta=\left(\mathrm{2}{m}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\left({m}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{1}+\mathrm{4}{R}^{\mathrm{2}} −\mathrm{4}{m}=\mathrm{0} \\ $$$$\Rightarrow{m}=\frac{\mathrm{1}}{\mathrm{4}}+{R}^{\mathrm{2}} \\ $$$${Center}\:{of}\:{circle}\:{with}\:{radius}\:{b}\:{is} \\ $$$${B}\left(\mathrm{0},{m}+{R}+{b}\right) \\ $$$${x}^{\mathrm{2}} +\left({y}−{m}−{R}−{b}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$${y}+\left[{y}−\left(\frac{\mathrm{1}}{\mathrm{4}}+{R}^{\mathrm{2}} +{R}+{b}\right)\right]^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} −\mathrm{2}\left({R}^{\mathrm{2}} +{R}+{b}−\frac{\mathrm{1}}{\mathrm{4}}\right){y}+\left({R}^{\mathrm{2}} +{R}+{b}+\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Delta=\left({R}^{\mathrm{2}} +{R}+{b}−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} −\left({R}^{\mathrm{2}} +{R}+{b}+\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{0} \\ $$$${b}^{\mathrm{2}} −{b}−\left({R}^{\mathrm{2}} +{R}\right)=\mathrm{0} \\ $$$$\Rightarrow{b}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{2}{R}+\mathrm{1}\right)={R}+\mathrm{1} \\ $$$$ \\ $$$${Center}\:{of}\:{circle}\:{with}\:{radius}\:{a}\:{is} \\ $$$${A}\left(\mathrm{2}\sqrt{{Ra}},{m}+{R}−{a}\right) \\ $$$${it}\:{touches}\:{the}\:{parabola}\:{at}\:{P}\left({p},\:{p}^{\mathrm{2}} \right). \\ $$$$\mathrm{tan}\:\theta=\mathrm{2}{p}=\frac{\mathrm{2}\sqrt{{Ra}}}{{a}−{R}} \\ $$$$\Rightarrow{p}=\frac{\sqrt{{Ra}}}{{a}−{R}} \\ $$$$\left(\mathrm{2}\sqrt{{Ra}}−{p}\right)^{\mathrm{2}} +\left({m}+{R}−{a}−{p}^{\mathrm{2}} \right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\left(\mathrm{2}\sqrt{{Ra}}−\frac{\sqrt{{Ra}}}{{a}−{R}}\right)^{\mathrm{2}} +\left[{m}+{R}−{a}−\frac{{Ra}}{\left({a}−{R}\right)^{\mathrm{2}} }\right]^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\left[\mathrm{2}−\frac{\mathrm{1}}{{R}\left(\frac{{a}}{{R}}−\mathrm{1}\right)}\right]^{\mathrm{2}} \left(\frac{{a}}{{R}}\right)+\frac{\mathrm{1}}{{R}^{\mathrm{2}} }\left[{m}−{R}\left(\frac{{a}}{{R}}−\mathrm{1}\right)−\frac{\frac{{a}}{{R}}}{\left(\frac{{a}}{{R}}−\mathrm{1}\right)^{\mathrm{2}} }\right]^{\mathrm{2}} =\left(\frac{{a}}{{R}}\right)^{\mathrm{2}} \\ $$$$\left[\mathrm{2}−\frac{\mathrm{1}}{{R}\left(\xi−\mathrm{1}\right)}\right]^{\mathrm{2}} \xi+\frac{\mathrm{1}}{{R}^{\mathrm{2}} }\left[\frac{\mathrm{1}}{\mathrm{4}}+{R}^{\mathrm{2}} −{R}\left(\xi−\mathrm{1}\right)−\frac{\xi}{\left(\xi−\mathrm{1}\right)^{\mathrm{2}} }\right]^{\mathrm{2}} =\xi^{\mathrm{2}} \\ $$$$\Rightarrow\xi=... \\ $$$$ \\ $$$${Center}\:{of}\:{circle}\:{with}\:{radius}\:{c}\:{is} \\ $$$${C}\left(\mathrm{2}\sqrt{{Rc}},{m}+{R}−{c}\right) \\ $$$${it}\:{touches}\:{the}\:{parabola}\:{at}\:{Q}\left({q},\:{q}^{\mathrm{2}} \right). \\ $$$$\mathrm{tan}\:\varphi=\mathrm{2}{q} \\ $$$${q}=\mathrm{2}\sqrt{{Rc}}+{c}\:\mathrm{sin}\:\varphi=\mathrm{2}\sqrt{{Rc}}+\frac{\mathrm{2}{cq}}{\sqrt{\mathrm{1}+\mathrm{4}{q}^{\mathrm{2}} }} \\ $$$$\Rightarrow{q}−\mathrm{2}\sqrt{{Rc}}=\frac{\mathrm{2}{cq}}{\sqrt{\mathrm{1}+\mathrm{4}{q}^{\mathrm{2}} }}\:\:\:...\left({i}\right) \\ $$$${q}^{\mathrm{2}} ={m}+{R}−{c}−{c}\:\mathrm{cos}\:\varphi={m}+{R}−{c}−\frac{{c}}{\sqrt{\mathrm{1}+\mathrm{4}{q}^{\mathrm{2}} }} \\ $$$$\Rightarrow{m}+{R}−{c}−{q}^{\mathrm{2}} =\frac{{c}}{\sqrt{\mathrm{1}+\mathrm{4}{q}^{\mathrm{2}} }}\:\:\:\:...\left({ii}\right) \\ $$$${q}−\mathrm{2}\sqrt{{Rc}}=\mathrm{2}{q}\left({m}+{R}−{c}−{q}^{\mathrm{2}} \right) \\ $$$${q}^{\mathrm{3}} −\left({R}^{\mathrm{2}} +{R}−{c}−\frac{\mathrm{1}}{\mathrm{4}}\right){q}−\sqrt{{Rc}}=\mathrm{0} \\ $$$$\Rightarrow{q}=\sqrt[{\mathrm{3}}]{\frac{\sqrt{{Rc}}}{\mathrm{2}}+\sqrt{\frac{{Rc}}{\mathrm{4}}−\frac{\left({R}^{\mathrm{2}} +{R}−{c}−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}} }{\mathrm{27}}}}+\sqrt[{\mathrm{3}}]{\frac{\sqrt{{Rc}}}{\mathrm{2}}−\sqrt{\frac{{Rc}}{\mathrm{4}}−\frac{\left({R}^{\mathrm{2}} +{R}−{c}−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}} }{\mathrm{27}}}} \\ $$$${put}\:{this}\:{into}\:\left({i}\right)\:{or}\:\left({ii}\right)\:{to}\:{get}\:{c} \\ $$
Commented by mr W last updated on 05/Jul/20

Commented by ajfour last updated on 05/Jul/20
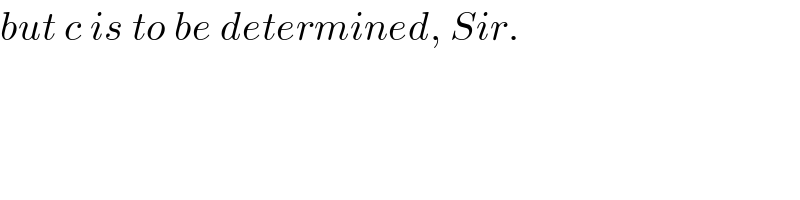
$${but}\:{c}\:{is}\:{to}\:{be}\:{determined},\:{Sir}. \\ $$
Commented by mr W last updated on 05/Jul/20
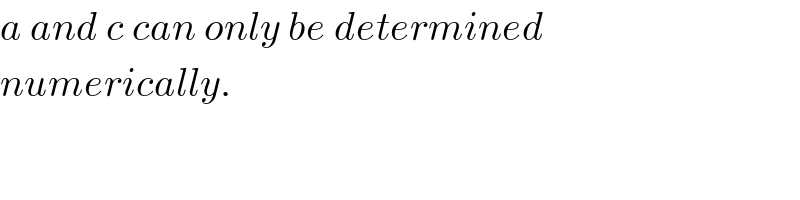
$${a}\:{and}\:{c}\:{can}\:{only}\:{be}\:{determined}\: \\ $$$${numerically}. \\ $$
Commented by ajfour last updated on 05/Jul/20

$${if}\:{we}\:{discuss},\:{i}\:{think}\:{we}\:{can}\:{get}\:{the} \\ $$$${expression}\:{for}\:{radii}\:{a}\:{and}\:{c}\:,\:{Sir}.. \\ $$
Commented by mr W last updated on 05/Jul/20

$${i}\:{found}\:{no}\:{way}\:{to}\:{get}\:{them}. \\ $$
Commented by ajfour last updated on 06/Jul/20

$$\:\:\:\:{Sir}\:{i}\:{got}\:\:{a}={R}\left({R}+\mathrm{1}/\mathrm{2}\right)/\left({R}−\mathrm{1}/\mathrm{2}\right) \\ $$$${Expression}\:{for}\:{c}\:{indeed}\:{seems} \\ $$$${difficult}. \\ $$
Commented by mr W last updated on 06/Jul/20

$${you}\:{got}\:{it}\:{at}\:{least}\:{for}\:{a}!\:{it}'{s}\:{correct}. \\ $$
