Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 101742 by bemath last updated on 04/Jul/20

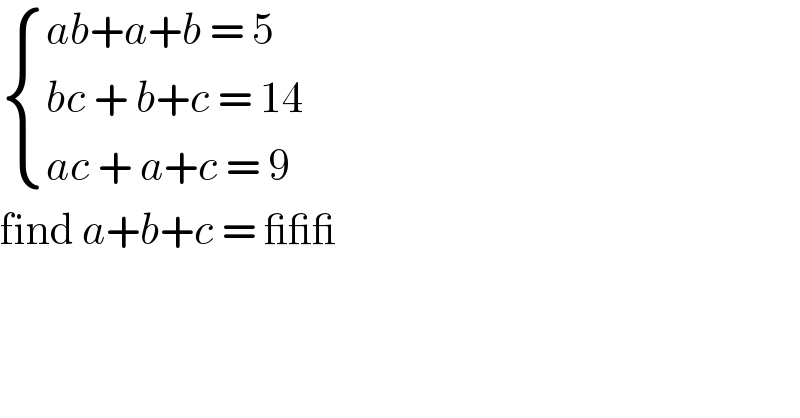
{ ((ab+a+b = 5)),((bc + b+c = 14)),((ac + a+c = 9)) :} find a+b+c = ___

$$\begin{cases}{{ab}+{a}+{b}\:=\:\mathrm{5}}\\{{bc}\:+\:{b}+{c}\:=\:\mathrm{14}}\\{{ac}\:+\:{a}+{c}\:=\:\mathrm{9}}\end{cases} \\ $$$$\mathrm{find}\:{a}+{b}+{c}\:=\:\_\_\_ \\ $$

Answered by bramlex last updated on 04/Jul/20

(1) a = ((5−b)/(b+1)) = ((9−c)/(c+1)) (2) b = ((14−c)/(c+1)) (3) ((5−(((14−c)/(c+1))))/(1+(((14−c)/(c+1))))) = ((9−c)/(c+1)) ((5c+5−14+c)/(c+1+14−c)) = ((9−c)/(c+1)) ((6c−9)/(15)) = ((9−c)/(c+1)) ⇔ ((2c−3)/5) = ((9−c)/(c+1)) (2c−3)(c+1) = 45−5c 2c^2 −c−3+5c−45 = 0 2c^2 +4c−48=0; c^2 +2c−24=0 (c+6)(c−4)=0 { ((c=4 ∧a = 1 ∧ b=2 ⇒ a+b+c = 7)),((c=−6∧a=−3∧b= −4⇒a+b+c =−13)) :} (Bramlex ⊕)

$$\left(\mathrm{1}\right)\:{a}\:=\:\frac{\mathrm{5}−{b}}{{b}+\mathrm{1}}\:=\:\frac{\mathrm{9}−{c}}{{c}+\mathrm{1}} \\ $$$$\left(\mathrm{2}\right)\:{b}\:=\:\frac{\mathrm{14}−{c}}{{c}+\mathrm{1}}\: \\ $$$$\left(\mathrm{3}\right)\:\:\frac{\mathrm{5}−\left(\frac{\mathrm{14}−{c}}{{c}+\mathrm{1}}\right)}{\mathrm{1}+\left(\frac{\mathrm{14}−{c}}{{c}+\mathrm{1}}\right)}\:=\:\frac{\mathrm{9}−{c}}{{c}+\mathrm{1}} \\ $$$$\frac{\mathrm{5}{c}+\mathrm{5}−\mathrm{14}+{c}}{{c}+\mathrm{1}+\mathrm{14}−{c}}\:=\:\frac{\mathrm{9}−{c}}{{c}+\mathrm{1}} \\ $$$$\frac{\mathrm{6}{c}−\mathrm{9}}{\mathrm{15}}\:=\:\frac{\mathrm{9}−{c}}{{c}+\mathrm{1}}\:\Leftrightarrow\:\frac{\mathrm{2}{c}−\mathrm{3}}{\mathrm{5}}\:=\:\frac{\mathrm{9}−{c}}{{c}+\mathrm{1}} \\ $$$$\left(\mathrm{2}{c}−\mathrm{3}\right)\left({c}+\mathrm{1}\right)\:=\:\mathrm{45}−\mathrm{5}{c} \\ $$$$\mathrm{2}{c}^{\mathrm{2}} −{c}−\mathrm{3}+\mathrm{5}{c}−\mathrm{45}\:=\:\mathrm{0} \\ $$$$\mathrm{2}{c}^{\mathrm{2}} +\mathrm{4}{c}−\mathrm{48}=\mathrm{0};\:{c}^{\mathrm{2}} +\mathrm{2}{c}−\mathrm{24}=\mathrm{0} \\ $$$$\left({c}+\mathrm{6}\right)\left({c}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\begin{cases}{{c}=\mathrm{4}\:\wedge{a}\:=\:\mathrm{1}\:\wedge\:{b}=\mathrm{2}\:\Rightarrow\:{a}+{b}+{c}\:=\:\mathrm{7}}\\{{c}=−\mathrm{6}\wedge{a}=−\mathrm{3}\wedge{b}=\:−\mathrm{4}\Rightarrow{a}+{b}+{c}\:=−\mathrm{13}}\end{cases} \\ $$$$\left(\mathcal{B}\mathrm{ramlex}\:\oplus\right)\: \\ $$$$ \\ $$

Answered by nimnim last updated on 04/Jul/20

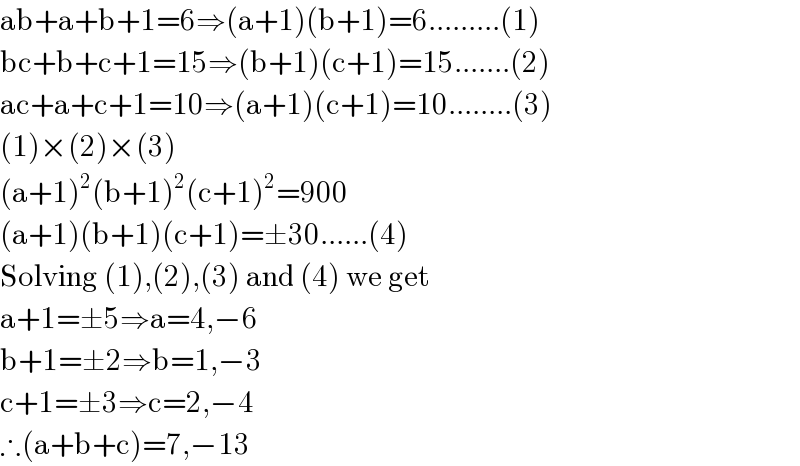
ab+a+b+1=6⇒(a+1)(b+1)=6.........(1) bc+b+c+1=15⇒(b+1)(c+1)=15.......(2) ac+a+c+1=10⇒(a+1)(c+1)=10........(3) (1)×(2)×(3) (a+1)^2 (b+1)^2 (c+1)^2 =900 (a+1)(b+1)(c+1)=±30......(4) Solving (1),(2),(3) and (4) we get a+1=±5⇒a=4,−6 b+1=±2⇒b=1,−3 c+1=±3⇒c=2,−4 ∴(a+b+c)=7,−13

$$\mathrm{ab}+\mathrm{a}+\mathrm{b}+\mathrm{1}=\mathrm{6}\Rightarrow\left(\mathrm{a}+\mathrm{1}\right)\left(\mathrm{b}+\mathrm{1}\right)=\mathrm{6}.........\left(\mathrm{1}\right) \\ $$$$\mathrm{bc}+\mathrm{b}+\mathrm{c}+\mathrm{1}=\mathrm{15}\Rightarrow\left(\mathrm{b}+\mathrm{1}\right)\left(\mathrm{c}+\mathrm{1}\right)=\mathrm{15}.......\left(\mathrm{2}\right) \\ $$$$\mathrm{ac}+\mathrm{a}+\mathrm{c}+\mathrm{1}=\mathrm{10}\Rightarrow\left(\mathrm{a}+\mathrm{1}\right)\left(\mathrm{c}+\mathrm{1}\right)=\mathrm{10}........\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{1}\right)×\left(\mathrm{2}\right)×\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{a}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{b}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{c}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{900} \\ $$$$\left(\mathrm{a}+\mathrm{1}\right)\left(\mathrm{b}+\mathrm{1}\right)\left(\mathrm{c}+\mathrm{1}\right)=\pm\mathrm{30}......\left(\mathrm{4}\right) \\ $$$$\mathrm{Solving}\:\left(\mathrm{1}\right),\left(\mathrm{2}\right),\left(\mathrm{3}\right)\:\mathrm{and}\:\left(\mathrm{4}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{a}+\mathrm{1}=\pm\mathrm{5}\Rightarrow\mathrm{a}=\mathrm{4},−\mathrm{6} \\ $$$$\mathrm{b}+\mathrm{1}=\pm\mathrm{2}\Rightarrow\mathrm{b}=\mathrm{1},−\mathrm{3} \\ $$$$\mathrm{c}+\mathrm{1}=\pm\mathrm{3}\Rightarrow\mathrm{c}=\mathrm{2},−\mathrm{4} \\ $$$$\therefore\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)=\mathrm{7},−\mathrm{13} \\ $$

Commented by Rasheed.Sindhi last updated on 04/Jul/20

Cool!

$$\mathcal{C}{ool}! \\ $$

Answered by 1549442205 last updated on 04/Jul/20

(1)⇔(a+1)(b+1)=6 (2)⇔(b+1)(c+1)=15 (3)⇔(c+1)(a+1)=10 [(a+1)(b+1)(c+1)]^2 =900⇔(a+1)(b+1)(c+1)=±30 ⇒ { ((a+1=±2)),((c+1=±5)),((b+1=±3)) :} ⇔(a,b,c)∈{(2,3,5);(−2,−3,−5)} a+b+c∈{7;−13}

$$\left(\mathrm{1}\right)\Leftrightarrow\left(\mathrm{a}+\mathrm{1}\right)\left(\mathrm{b}+\mathrm{1}\right)=\mathrm{6} \\ $$$$\left(\mathrm{2}\right)\Leftrightarrow\left(\mathrm{b}+\mathrm{1}\right)\left(\mathrm{c}+\mathrm{1}\right)=\mathrm{15} \\ $$$$\left(\mathrm{3}\right)\Leftrightarrow\left(\mathrm{c}+\mathrm{1}\right)\left(\mathrm{a}+\mathrm{1}\right)=\mathrm{10} \\ $$$$\left[\left(\mathrm{a}+\mathrm{1}\right)\left(\mathrm{b}+\mathrm{1}\right)\left(\mathrm{c}+\mathrm{1}\right)\right]^{\mathrm{2}} =\mathrm{900}\Leftrightarrow\left(\mathrm{a}+\mathrm{1}\right)\left(\mathrm{b}+\mathrm{1}\right)\left(\mathrm{c}+\mathrm{1}\right)=\pm\mathrm{30} \\ $$$$\Rightarrow\begin{cases}{\mathrm{a}+\mathrm{1}=\pm\mathrm{2}}\\{\mathrm{c}+\mathrm{1}=\pm\mathrm{5}}\\{\mathrm{b}+\mathrm{1}=\pm\mathrm{3}}\end{cases}\:\Leftrightarrow\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)\in\left\{\left(\mathrm{2},\mathrm{3},\mathrm{5}\right);\left(−\mathrm{2},−\mathrm{3},−\mathrm{5}\right)\right\} \\ $$$$\mathrm{a}+\mathrm{b}+\mathrm{c}\in\left\{\mathrm{7};−\mathrm{13}\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com