
Question Number 102060 by ajfour last updated on 06/Jul/20
Commented by ajfour last updated on 06/Jul/20

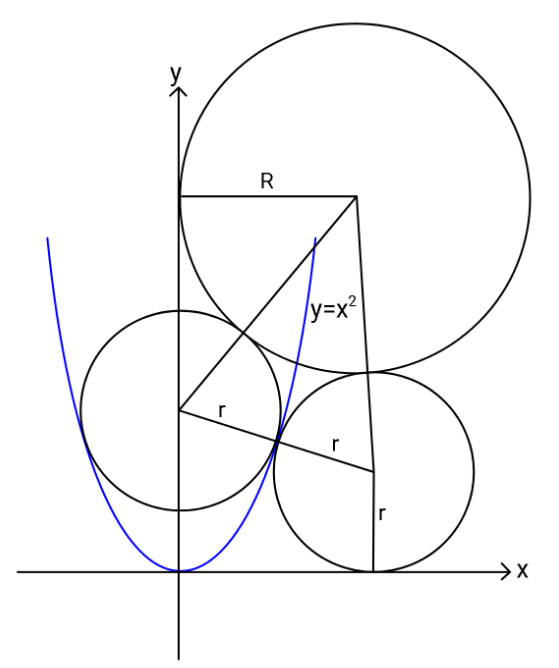
$${Find}\:\boldsymbol{{r}}\:{and}\:\boldsymbol{{R}}. \\ $$
Answered by mr W last updated on 06/Jul/20
![center of circle r inside M(0,m) m=(1/4)+r^2 center of circle r outside N((√(4r^2 −((1/4)+r^2 −r)^2 )),r) (1/2)(r+(1/4)+r^2 )=(1/4)[4r^2 −((1/4)+r^2 −r)^2 ] 2r^2 −2r−(1/2)=((1/4)+r^2 −r)^2 r^4 −2r^3 −(r^2 /2)+((3r)/2)+(9/(16))=0 (r−(3/2))^2 (r+(1/2))^2 =0 ⇒r=(3/2) center of circle R at (R,h) R^2 +(h−(1/4)−r^2 )^2 =(R+r)^2 ...(i) ((√(4r^2 −((1/4)+r^2 −r)^2 ))−R)^2 +(h−r)^2 =(R+r)^2 ...(ii) (i)−(ii): (2R−(√(4r^2 −((1/4)+r^2 −r)^2 )))(√(4r^2 −((1/4)+r^2 −r)^2 ))+(2h−(1/4)−r^2 −r)(−(1/4)−r^2 +r)=0 ⇒h=2((√2)R−1) R^2 +(2(√2)R−(9/2))^2 =(R+(3/2))^2 8R^2 −3(1+6(√2))R+18=0 ⇒oR=(3/(16))[1+6(√2)+(√(3(3+4(√2))))]](Q102140.png)
$${center}\:{of}\:{circle}\:{r}\:{inside}\:{M}\left(\mathrm{0},{m}\right) \\ $$$${m}=\frac{\mathrm{1}}{\mathrm{4}}+{r}^{\mathrm{2}} \\ $$$${center}\:{of}\:{circle}\:{r}\:{outside}\:{N}\left(\sqrt{\mathrm{4}{r}^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{4}}+{r}^{\mathrm{2}} −{r}\right)^{\mathrm{2}} },{r}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({r}+\frac{\mathrm{1}}{\mathrm{4}}+{r}^{\mathrm{2}} \right)=\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{4}{r}^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{4}}+{r}^{\mathrm{2}} −{r}\right)^{\mathrm{2}} \right] \\ $$$$\mathrm{2}{r}^{\mathrm{2}} −\mathrm{2}{r}−\frac{\mathrm{1}}{\mathrm{2}}=\left(\frac{\mathrm{1}}{\mathrm{4}}+{r}^{\mathrm{2}} −{r}\right)^{\mathrm{2}} \\ $$$${r}^{\mathrm{4}} −\mathrm{2}{r}^{\mathrm{3}} −\frac{{r}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{3}{r}}{\mathrm{2}}+\frac{\mathrm{9}}{\mathrm{16}}=\mathrm{0} \\ $$$$\left({r}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} \left({r}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{r}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$ \\ $$$${center}\:{of}\:{circle}\:{R}\:{at}\:\left({R},{h}\right) \\ $$$${R}^{\mathrm{2}} +\left({h}−\frac{\mathrm{1}}{\mathrm{4}}−{r}^{\mathrm{2}} \right)^{\mathrm{2}} =\left({R}+{r}\right)^{\mathrm{2}} \:\:\:...\left({i}\right) \\ $$$$\left(\sqrt{\mathrm{4}{r}^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{4}}+{r}^{\mathrm{2}} −{r}\right)^{\mathrm{2}} }−{R}\right)^{\mathrm{2}} +\left({h}−{r}\right)^{\mathrm{2}} =\left({R}+{r}\right)^{\mathrm{2}} \:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\left(\mathrm{2}{R}−\sqrt{\mathrm{4}{r}^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{4}}+{r}^{\mathrm{2}} −{r}\right)^{\mathrm{2}} }\right)\sqrt{\mathrm{4}{r}^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{4}}+{r}^{\mathrm{2}} −{r}\right)^{\mathrm{2}} }+\left(\mathrm{2}{h}−\frac{\mathrm{1}}{\mathrm{4}}−{r}^{\mathrm{2}} −{r}\right)\left(−\frac{\mathrm{1}}{\mathrm{4}}−{r}^{\mathrm{2}} +{r}\right)=\mathrm{0} \\ $$$$\Rightarrow{h}=\mathrm{2}\left(\sqrt{\mathrm{2}}{R}−\mathrm{1}\right) \\ $$$${R}^{\mathrm{2}} +\left(\mathrm{2}\sqrt{\mathrm{2}}{R}−\frac{\mathrm{9}}{\mathrm{2}}\right)^{\mathrm{2}} =\left({R}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{8}{R}^{\mathrm{2}} −\mathrm{3}\left(\mathrm{1}+\mathrm{6}\sqrt{\mathrm{2}}\right){R}+\mathrm{18}=\mathrm{0} \\ $$$$\Rightarrow{oR}=\frac{\mathrm{3}}{\mathrm{16}}\left[\mathrm{1}+\mathrm{6}\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}\left(\mathrm{3}+\mathrm{4}\sqrt{\mathrm{2}}\right)}\right] \\ $$
Commented by mr W last updated on 06/Jul/20
Commented by ajfour last updated on 07/Jul/20

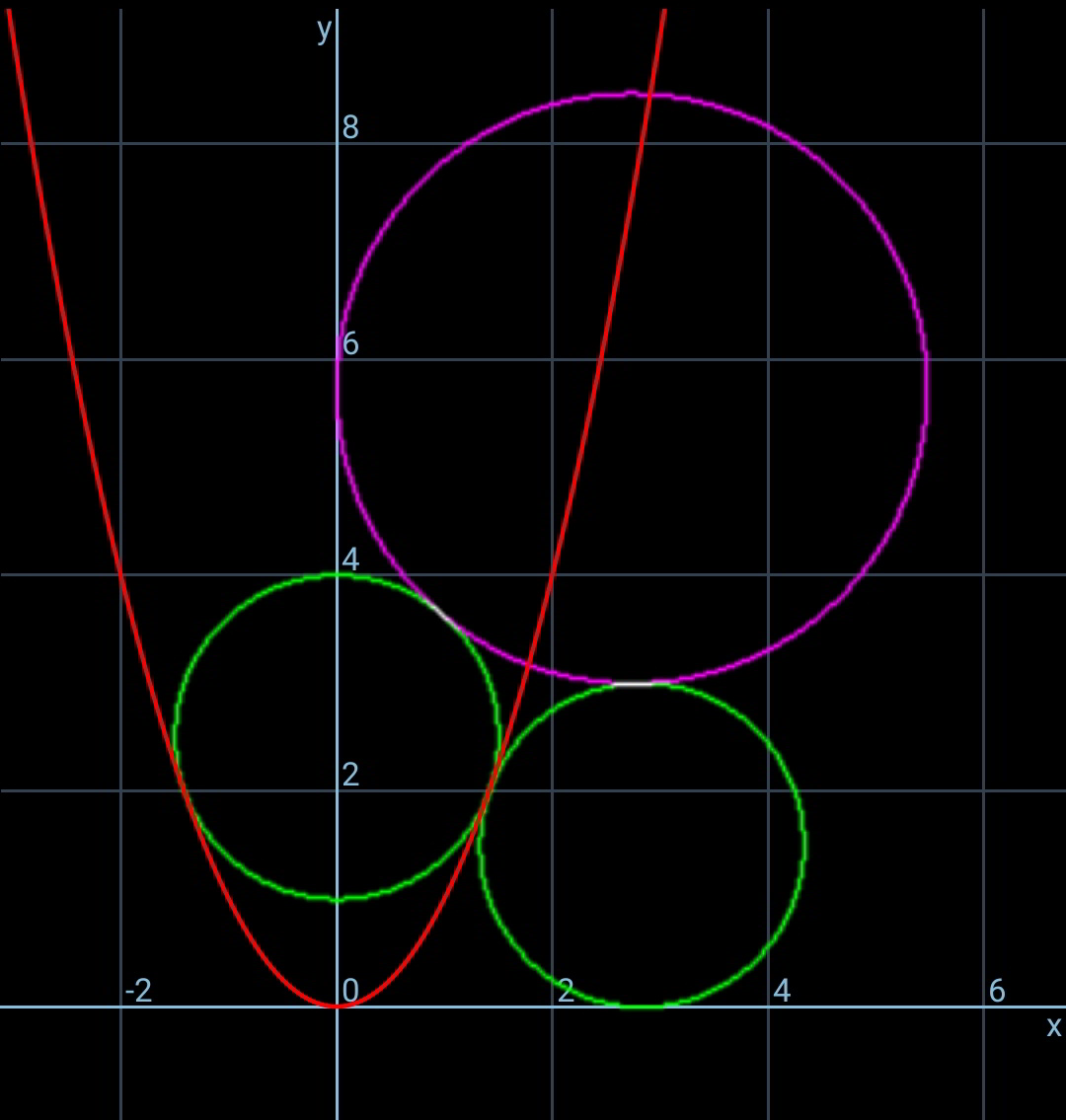
$${Thank}\:{you}\:{Sir},\:{Excellent}! \\ $$
Answered by ajfour last updated on 07/Jul/20
![let the smaller circles touch parabola at P(h,h^2 ) h=rsin θ , h^2 =r+rcos θ And 2h=tan θ ⇒ tan θ=2rsin θ ⇒ cos θ=(1/(2r)) & r^2 (1−(1/(4r^2 )))=r+(1/2) ⇒ r^2 −(1/4)=r+(1/2) r^2 −r−(3/4)=0 ⇒ r=(1/2)+(√((1/4)+(3/4))) r=(3/2) , cos θ=(1/3) center of left smaller circle be C. y_C = r+2rcos θ = (3/2)+1 = (5/2) Altitude of isosceles triangle H=(√((R+r)^2 −r^2 )) Hcos θ+rsin θ=R ⇒ (1/9)(R^2 +2Rr)=(R−(3/2)×((2(√2))/3))^2 ⇒ R^2 +3R=9[R^2 −2(√2)R+2] ⇒ 8R^2 −(18(√2)+3)R+18=0 R=((18(√2)+3)/(16))+(√((((18(√2)+3)/(16)))^2 −((18)/8))) R = (3/(16))(6(√2)+1+(√(9+12(√2)))) .](Q102180.png)
$${let}\:{the}\:{smaller}\:{circles}\:{touch}\:{parabola} \\ $$$${at}\:{P}\left({h},{h}^{\mathrm{2}} \right) \\ $$$${h}={r}\mathrm{sin}\:\theta\:\:\:,\:\:\:\:{h}^{\mathrm{2}} ={r}+{r}\mathrm{cos}\:\theta \\ $$$${And}\:\:\:\:\:\mathrm{2}{h}=\mathrm{tan}\:\theta \\ $$$$\Rightarrow\:\:\:\mathrm{tan}\:\theta=\mathrm{2}{r}\mathrm{sin}\:\theta\:\:\:\Rightarrow\:\:\:\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\mathrm{2}{r}} \\ $$$$\&\:\:\:\:\:{r}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}{r}^{\mathrm{2}} }\right)={r}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:{r}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}={r}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:{r}^{\mathrm{2}} −{r}−\frac{\mathrm{3}}{\mathrm{4}}=\mathrm{0}\:\:\:\:\Rightarrow\:\:{r}=\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$\:\:\:\:{r}=\frac{\mathrm{3}}{\mathrm{2}}\:\:\:\:\:\:\:,\:\:\:\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${center}\:{of}\:{left}\:{smaller}\:{circle}\:{be}\:{C}. \\ $$$${y}_{{C}} =\:{r}+\mathrm{2}{r}\mathrm{cos}\:\theta\:=\:\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{1}\:=\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\:\:{Altitude}\:{of}\:{isosceles}\:{triangle} \\ $$$$\:\:\:\:\:{H}=\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$${H}\mathrm{cos}\:\theta+{r}\mathrm{sin}\:\theta={R} \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{\mathrm{9}}\left({R}^{\mathrm{2}} +\mathrm{2}{Rr}\right)=\left({R}−\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:{R}^{\mathrm{2}} +\mathrm{3}{R}=\mathrm{9}\left[{R}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}{R}+\mathrm{2}\right] \\ $$$$\Rightarrow\:\:\:\:\mathrm{8}{R}^{\mathrm{2}} −\left(\mathrm{18}\sqrt{\mathrm{2}}+\mathrm{3}\right){R}+\mathrm{18}=\mathrm{0} \\ $$$$\:\:\:{R}=\frac{\mathrm{18}\sqrt{\mathrm{2}}+\mathrm{3}}{\mathrm{16}}+\sqrt{\left(\frac{\mathrm{18}\sqrt{\mathrm{2}}+\mathrm{3}}{\mathrm{16}}\right)^{\mathrm{2}} −\frac{\mathrm{18}}{\mathrm{8}}} \\ $$$$\:\:\:{R}\:=\:\frac{\mathrm{3}}{\mathrm{16}}\left(\mathrm{6}\sqrt{\mathrm{2}}+\mathrm{1}+\sqrt{\mathrm{9}+\mathrm{12}\sqrt{\mathrm{2}}}\right)\:. \\ $$
