Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 10223 by amir last updated on 30/Jan/17

Answered by mrW1 last updated on 03/Feb/17

to question 1: xy=1 y=(1/x) y′=−(1/x^2 ) let B a point on the curve and AB is a orthogonal line to the curve. let point B have the coordinates (t, s). s=(1/t) the slope of tangent line on point B: m_t =y′(t)=−(1/t^2 ) the slope of the orthogonal line: m_o =−(1/m_t )=t^2 the equation of the orthogonal line: y−s=m_o (x−t) y−(1/t)=t^2 (x−t) since A(a,a) is a point on it, we get a−(1/t)=t^2 (a−t) t^4 −at^3 +at−1=0 (t+1)(t−1)(t^2 −at+1)=0 ⇒t_1 =−1 (point D) or ⇒t_2 =1 (point C) or ⇒t−at+1=0 ⇒⇒t_(3,4) =((a±(√(a^2 −4)))/2) if ∣a∣<2, t_(3,4) =unreal if ∣a∣=2, t_(3,4) =1=t_2 if ∣a∣>2, t_(3,4) =((a±(√(a^2 −4)))/2) (point B and B′) i.e. for any point A(a,a) there are at least 2 orthogonal lines (AC, AD). if ∣a∣>2, there are even 2 additional orthogonal lines (AB,AB′).

$${to}\:{question}\:\mathrm{1}: \\ $$$$ \\ $$$${xy}=\mathrm{1} \\ $$$${y}=\frac{\mathrm{1}}{{x}} \\ $$$${y}'=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$${let}\:{B}\:{a}\:{point}\:{on}\:{the}\:{curve}\:{and}\:{AB}\:{is} \\ $$$${a}\:{orthogonal}\:{line}\:{to}\:{the}\:{curve}. \\ $$$${let}\:{point}\:{B}\:{have}\:{the}\:{coordinates}\:\left({t},\:{s}\right). \\ $$$${s}=\frac{\mathrm{1}}{{t}} \\ $$$$ \\ $$$${the}\:{slope}\:{of}\:{tangent}\:{line}\:{on}\:{point}\:{B}: \\ $$$${m}_{{t}} ={y}'\left({t}\right)=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} } \\ $$$$ \\ $$$${the}\:{slope}\:{of}\:{the}\:{orthogonal}\:{line}: \\ $$$${m}_{{o}} =−\frac{\mathrm{1}}{{m}_{{t}} }={t}^{\mathrm{2}} \\ $$$$ \\ $$$${the}\:{equation}\:{of}\:{the}\:{orthogonal}\:{line}: \\ $$$${y}−{s}={m}_{{o}} \left({x}−{t}\right) \\ $$$${y}−\frac{\mathrm{1}}{{t}}={t}^{\mathrm{2}} \left({x}−{t}\right) \\ $$$$ \\ $$$${since}\:{A}\left({a},{a}\right)\:{is}\:{a}\:{point}\:{on}\:{it},\:{we}\:{get} \\ $$$${a}−\frac{\mathrm{1}}{{t}}={t}^{\mathrm{2}} \left({a}−{t}\right) \\ $$$${t}^{\mathrm{4}} −{at}^{\mathrm{3}} +{at}−\mathrm{1}=\mathrm{0} \\ $$$$\left({t}+\mathrm{1}\right)\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} −{at}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{t}_{\mathrm{1}} =−\mathrm{1}\:\left({point}\:{D}\right)\:{or} \\ $$$$\Rightarrow{t}_{\mathrm{2}} =\mathrm{1}\:\left({point}\:{C}\right)\:{or} \\ $$$$\Rightarrow{t}−{at}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\Rightarrow{t}_{\mathrm{3},\mathrm{4}} =\frac{{a}\pm\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}} \\ $$$${if}\:\mid{a}\mid<\mathrm{2},\:{t}_{\mathrm{3},\mathrm{4}} \:={unreal} \\ $$$${if}\:\mid{a}\mid=\mathrm{2},\:{t}_{\mathrm{3},\mathrm{4}} \:=\mathrm{1}={t}_{\mathrm{2}} \\ $$$${if}\:\mid{a}\mid>\mathrm{2},\:{t}_{\mathrm{3},\mathrm{4}} \:=\frac{{a}\pm\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\:\left({point}\:{B}\:{and}\:{B}'\right) \\ $$$$ \\ $$$${i}.{e}.\:{for}\:{any}\:{point}\:{A}\left({a},{a}\right)\:{there}\:{are} \\ $$$${at}\:{least}\:\mathrm{2}\:{orthogonal}\:{lines}\:\left({AC},\:{AD}\right). \\ $$$${if}\:\mid{a}\mid>\mathrm{2},\:{there}\:{are}\:{even}\:\mathrm{2}\:{additional} \\ $$$${orthogonal}\:{lines}\:\left({AB},{AB}'\right). \\ $$$$ \\ $$$$ \\ $$

Commented by mrW1 last updated on 02/Feb/17

Commented by amir last updated on 02/Feb/17

thank you so much.but Q no.2 and no.3 ?

$${thank}\:{you}\:{so}\:{much}.{but}\:{Q}\:{no}.\mathrm{2}\:{and}\:{no}.\mathrm{3}\:? \\ $$

Commented by amir last updated on 02/Feb/17

with which program i can draw this diagrams?

$${with}\:{which}\:{program}\:{i}\:{can}\:{draw}\:{this}\:\: \\ $$$${diagrams}? \\ $$

Commented by mrW1 last updated on 03/Feb/17

please try the app geogebra.

$${please}\:{try}\:{the}\:{app}\:{geogebra}. \\ $$

Answered by mrW1 last updated on 04/Feb/17

to question 2: if ∣a∣≤2, i.e. −2≤a≤2, there are only 2 orthogonal lines from point A: AD with slope = 45° AC with slope = 45° the angel between them is 0°. if ∣a∣>2, i.e. a<−2 or a>2, there are 4 orthogonal lines from point A: AD with slope = 45° AC with slope = 45° the angel between them is 0°. AB with slope angel, lets say α_1 AB′ with slope angel, lets say α_2 the angel between them is, lets say α α=α_1 −α_2 tan α_1 =−(1/(f′(t_3 )))=t_3 ^2 =(((a+(√(a^2 −4)))/2))^2 tan α_2 =−(1/(f′(t_4 )))=t_4 ^2 =(((a−(√(a^2 −4)))/2))^2 tan α=tan (α_1 −α_2 )=((tan α_1 −tan α_2 )/(1+tan _1 tan α_2 )) =(((((a+(√(a^2 −4)))/2))^2 −(((a−(√(a^2 −4)))/2))^2 )/(1+(((a+(√(a^2 −4)))/2))^2 (((a−(√(a^2 −4)))/2))^2 )) =4×(((a+(√(a^2 −4)))^2 −(a−(√(a^2 −4)))^2 )/(16+(a+(√(a^2 −4)))^2 (a−(√(a^2 −4)))^2 )) =4×(((a+(√(a^2 −4))+a−(√(a^2 −4)))(a+(√(a^2 −4))−a+(√(a^2 −4))))/(16+(a^2 −a^2 +4)^2 )) =4×(((2a)(2(√(a^2 −4))))/(32)) =((a(√(a^2 −4)))/2) α=tan^(−1) (((a(√(a^2 −4)))/2))

$${to}\:{question}\:\mathrm{2}: \\ $$$$ \\ $$$${if}\:\mid{a}\mid\leqslant\mathrm{2},\:{i}.{e}.\:−\mathrm{2}\leqslant{a}\leqslant\mathrm{2},\:{there}\:{are}\:{only} \\ $$$$\mathrm{2}\:{orthogonal}\:{lines}\:{from}\:{point}\:{A}: \\ $$$${AD}\:{with}\:{slope}\:=\:\mathrm{45}° \\ $$$${AC}\:{with}\:{slope}\:=\:\mathrm{45}° \\ $$$${the}\:{angel}\:{between}\:{them}\:{is}\:\mathrm{0}°. \\ $$$$ \\ $$$${if}\:\mid{a}\mid>\mathrm{2},\:{i}.{e}.\:{a}<−\mathrm{2}\:{or}\:{a}>\mathrm{2},\:{there}\:{are} \\ $$$$\mathrm{4}\:{orthogonal}\:{lines}\:{from}\:{point}\:{A}: \\ $$$${AD}\:{with}\:{slope}\:=\:\mathrm{45}° \\ $$$${AC}\:{with}\:{slope}\:=\:\mathrm{45}° \\ $$$${the}\:{angel}\:{between}\:{them}\:{is}\:\mathrm{0}°. \\ $$$${AB}\:{with}\:{slope}\:{angel},\:{lets}\:{say}\:\alpha_{\mathrm{1}} \\ $$$${AB}'\:{with}\:{slope}\:{angel},\:{lets}\:{say}\:\alpha_{\mathrm{2}} \\ $$$${the}\:{angel}\:{between}\:{them}\:{is},\:{lets}\:{say}\:\alpha \\ $$$$\alpha=\alpha_{\mathrm{1}} −\alpha_{\mathrm{2}} \\ $$$$\mathrm{tan}\:\alpha_{\mathrm{1}} =−\frac{\mathrm{1}}{{f}'\left({t}_{\mathrm{3}} \right)}={t}_{\mathrm{3}} ^{\mathrm{2}} =\left(\frac{{a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{tan}\:\alpha_{\mathrm{2}} =−\frac{\mathrm{1}}{{f}'\left({t}_{\mathrm{4}} \right)}={t}_{\mathrm{4}} ^{\mathrm{2}} =\left(\frac{{a}−\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{tan}\:\alpha=\mathrm{tan}\:\left(\alpha_{\mathrm{1}} −\alpha_{\mathrm{2}} \right)=\frac{\mathrm{tan}\:\alpha_{\mathrm{1}} −\mathrm{tan}\:\alpha_{\mathrm{2}} }{\mathrm{1}+\mathrm{tan}\:_{\mathrm{1}} \mathrm{tan}\:\alpha_{\mathrm{2}} } \\ $$$$=\frac{\left(\frac{{a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{{a}−\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{1}+\left(\frac{{a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} \left(\frac{{a}−\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{4}×\frac{\left({a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}\right)^{\mathrm{2}} −\left({a}−\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}\right)^{\mathrm{2}} }{\mathrm{16}+\left({a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}\right)^{\mathrm{2}} \left({a}−\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}\right)^{\mathrm{2}} }\: \\ $$$$=\mathrm{4}×\frac{\left({a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}+{a}−\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}\right)\left({a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}−{a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}\right)}{\mathrm{16}+\left({a}^{\mathrm{2}} −{a}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{4}×\frac{\left(\mathrm{2}{a}\right)\left(\mathrm{2}\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}\right)}{\mathrm{32}} \\ $$$$=\frac{{a}\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}} \\ $$$$\alpha=\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\right) \\ $$

Commented by amir last updated on 04/Feb/17

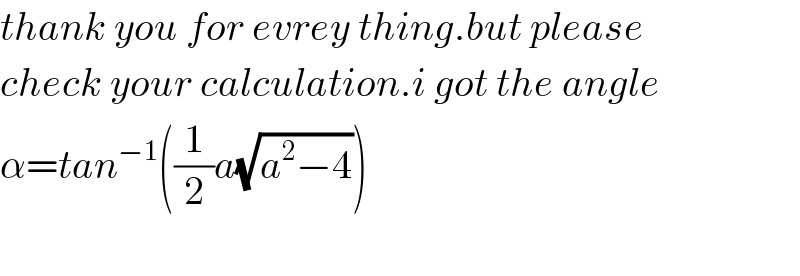
thank you for evrey thing.but please check your calculation.i got the angle α=tan^(−1) ((1/2)a(√(a^2 −4)))

$${thank}\:{you}\:{for}\:{evrey}\:{thing}.{but}\:{please} \\ $$$${check}\:{your}\:{calculation}.{i}\:{got}\:{the}\:{angle} \\ $$$$\alpha={tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}{a}\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}\right) \\ $$$$ \\ $$

Commented by mrW1 last updated on 04/Feb/17

your are right. it is fixed now. thank you!

$${your}\:{are}\:{right}.\:{it}\:{is}\:{fixed}\:{now}.\:{thank}\:{you}! \\ $$

Commented by mrW1 last updated on 04/Feb/17

what about Q1 and Q2 if we have point A(a,−a)?

$${what}\:{about}\:{Q}\mathrm{1}\:{and}\:{Q}\mathrm{2}\:{if}\:{we}\:{have}\:{point}\:{A}\left({a},−{a}\right)? \\ $$

Commented by amir last updated on 08/Feb/17

in case of point B(a,−a) ,there are only 2 perpendiculare lines. y=(1/x)⇒y^′ =−(1/x^2 )⇒m_t =−(1/t^2 ),m_p =+t^2 that M(t,(1/t)) and N(s,(1/s)) are the intersection points of the curve and the per.lines. olso m_p be the slope of per_ .line y−y_M =m_p (x−x_M )⇒y−(1/t)=t^2 (x−t) −a−(1/t)=t^2 (a−t)⇒t^4 −at^3 −at−1=0 (t^2 +1)(t^2 −at−1)=0, t^2 +1≠0 ⇒t=((a±(√(a^2 +4)))/2)⇒ (((M(((a+(√(a^2 +4)))/2),((a−(√(a^2 +4)))/(−2))))),((N(((a−(√(a^2 +4)))/2),((a+(√(a^2 +4)))/(−2))))) ) m_(BN) =((−a−((a+(√(a^2 +4)))/(−2)))/(a−((a−(√(a^2 +4)))/2)))=(1/4)(a−(√(a^2 +4)))^2 m_(BM) =((−a−((a−(√(a^2 +4)))/(−2)))/(a−((a+(√(a^2 +4)))/2)))=(1/4)(a+(√(a^2 +4)))^2 tan α=∣((m_(BN) −m_(BM) )/(1+m_(BN) ×m_(BM) ))∣= ∣(((1/4)(a−(√(a^2 +4)))^2 −(1/4)(a+(√(a^2 +4)))^2 )/(1+(1/4)(a−(√(a^2 +4)))^2 ×(1/4)(a+(√(a^2 +4)))^2 ))∣=(1/2)a(√(a^2 +4)) α=tan^(−1) ((1/2)a(√(a^2 +4))) ■

$${in}\:{case}\:{of}\:{point}\:\boldsymbol{{B}}\left({a},−{a}\right)\:,{there}\:{are} \\ $$$${only}\:\mathrm{2}\:{perpendiculare}\:{lines}. \\ $$$${y}=\frac{\mathrm{1}}{{x}}\Rightarrow{y}^{'} =−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\Rightarrow{m}_{{t}} =−\frac{\mathrm{1}}{{t}^{\mathrm{2}} },{m}_{{p}} =+{t}^{\mathrm{2}} \\ $$$${that}\:{M}\left({t},\frac{\mathrm{1}}{{t}}\right)\:\:{and}\:{N}\left({s},\frac{\mathrm{1}}{{s}}\right)\:{are}\:{the}\:{intersection}\:{points} \\ $$$${of}\:{the}\:{curve}\:{and}\:{the}\:{per}.{lines}. \\ $$$${olso}\:{m}_{{p}} \:{be}\:{the}\:{slope}\:{of}\:{pe}\underset{} {{r}}.{line} \\ $$$${y}−{y}_{{M}} ={m}_{{p}} \left({x}−{x}_{{M}} \right)\Rightarrow{y}−\frac{\mathrm{1}}{{t}}={t}^{\mathrm{2}} \left({x}−{t}\right) \\ $$$$−{a}−\frac{\mathrm{1}}{{t}}={t}^{\mathrm{2}} \left({a}−{t}\right)\Rightarrow{t}^{\mathrm{4}} −{at}^{\mathrm{3}} −{at}−\mathrm{1}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −{at}−\mathrm{1}\right)=\mathrm{0},\:{t}^{\mathrm{2}} +\mathrm{1}\neq\mathrm{0} \\ $$$$\Rightarrow{t}=\frac{{a}\pm\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\Rightarrow\begin{pmatrix}{{M}\left(\frac{{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}},\frac{{a}−\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{−\mathrm{2}}\right)}\\{{N}\left(\frac{{a}−\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}},\frac{{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{−\mathrm{2}}\right)}\end{pmatrix} \\ $$$$\boldsymbol{{m}}_{\boldsymbol{{BN}}} =\frac{−\boldsymbol{{a}}−\frac{\boldsymbol{{a}}+\sqrt{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{4}}}{−\mathrm{2}}}{\boldsymbol{{a}}−\frac{\boldsymbol{{a}}−\sqrt{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{4}}\left(\boldsymbol{{a}}−\sqrt{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{4}}\right)^{\mathrm{2}} \\ $$$$\boldsymbol{{m}}_{\boldsymbol{{BM}}} =\frac{−\boldsymbol{{a}}−\frac{\boldsymbol{{a}}−\sqrt{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{4}}}{−\mathrm{2}}}{\boldsymbol{{a}}−\frac{\boldsymbol{{a}}+\sqrt{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{4}}\left(\boldsymbol{{a}}+\sqrt{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{4}}\right)^{\mathrm{2}} \\ $$$$\mathrm{tan}\:\alpha=\mid\frac{\boldsymbol{{m}}_{\boldsymbol{{B}}{N}} −\boldsymbol{{m}}_{\boldsymbol{{BM}}} }{\mathrm{1}+\boldsymbol{{m}}_{\boldsymbol{{BN}}} ×\boldsymbol{{m}}_{\boldsymbol{{BM}}} }\mid= \\ $$$$\mid\frac{\frac{\mathrm{1}}{\mathrm{4}}\left(\boldsymbol{{a}}−\sqrt{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{4}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\left(\boldsymbol{{a}}+\sqrt{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{4}}\right)^{\mathrm{2}} }{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\left(\boldsymbol{{a}}−\sqrt{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{4}}\right)^{\mathrm{2}} ×\frac{\mathrm{1}}{\mathrm{4}}\left(\boldsymbol{{a}}+\sqrt{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{4}}\right)^{\mathrm{2}} }\mid=\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{a}}\sqrt{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{4}} \\ $$$$\alpha=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{a}}\sqrt{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{4}}\right)\:\blacksquare \\ $$

Commented by amir last updated on 07/Feb/17

Commented by amir last updated on 07/Feb/17

dear mrW1! please draw a nice diagram with geogebra and post it here.tnx.

$${dear}\:{mrW}\mathrm{1}!\:{please}\:{draw}\:{a}\:{nice}\:{diagram} \\ $$$${with}\:{geogebra}\:{and}\:{post}\:{it}\:{here}.{tnx}. \\ $$

Commented by mrW1 last updated on 08/Feb/17

Commented by amir last updated on 08/Feb/17

thank you very much mrw1. you are a real mathmatic man. goodlock!

$${thank}\:{you}\:{very}\:{much}\:{mrw}\mathrm{1}. \\ $$$${you}\:{are}\:{a}\:{real}\:{mathmatic}\:{man}. \\ $$$${goodlock}! \\ $$

Answered by mrW1 last updated on 03/Feb/17

to question 3: if ∣a∣≤2, there are 2 orthogonal lines from A. the area between them and the curve is 0. if ∣a∣>2, there are 4 orthogonal lines from A. F_1 =area of ARPB′ F_2 =area of ARQB F_3 =area of B′BQP F=area between orthogonal lines and the curve, ABB′. F=F_1 −F_2 −F_3 F_1 =(1/2)(a+y_4 )(a−x_4 )=(1/2)(a+(1/t_4 ))(a−t_4 )=(1/2)(a+(2/(a−(√(a^2 −4)))))(a+((a−(√(a^2 −4)))/2)) F_2 =(1/2)(a+y_3 )(a−x_3 )=(1/2)(a+(1/t_3 ))(a−t_3 )=(1/2)(a+(2/(a+(√(a^2 −4)))))(a+((a+(√(a^2 −4)))/2)) F_3 =∫_(x_4 ) ^x_3 (1/x)dx=(ln ∣x∣)∣_t_4 ^t_3 =ln ∣(t_3 /t_4 )∣=ln ∣((a+(√(a^2 −4)))/(a−(√(a^2 −4))))∣ F=(1/2)(a+(2/(a−(√(a^2 −4)))))(a+((a−(√(a^2 −4)))/2))−(1/2)(a+(2/(a+(√(a^2 −4)))))(a+((a+(√(a^2 −4)))/2))−ln ∣((a+(√(a^2 −4)))/(a−(√(a^2 −4))))∣

$${to}\:{question}\:\mathrm{3}: \\ $$$$ \\ $$$${if}\:\mid{a}\mid\leqslant\mathrm{2},\:{there}\:{are}\:\mathrm{2}\:{orthogonal}\:{lines} \\ $$$${from}\:{A}.\:{the}\:{area}\:{between}\:{them}\:{and} \\ $$$${the}\:{curve}\:{is}\:\mathrm{0}. \\ $$$$ \\ $$$${if}\:\mid{a}\mid>\mathrm{2},\:{there}\:{are}\:\mathrm{4}\:{orthogonal}\:{lines} \\ $$$${from}\:{A}. \\ $$$${F}_{\mathrm{1}} ={area}\:{of}\:{ARPB}' \\ $$$${F}_{\mathrm{2}} ={area}\:{of}\:{ARQB} \\ $$$${F}_{\mathrm{3}} ={area}\:{of}\:{B}'{BQP} \\ $$$${F}={area}\:{between}\:{orthogonal}\:{lines}\: \\ $$$$\:\:\:\:\:\:\:\:{and}\:{the}\:{curve},\:{ABB}'. \\ $$$${F}={F}_{\mathrm{1}} −{F}_{\mathrm{2}} −{F}_{\mathrm{3}} \\ $$$${F}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left({a}+{y}_{\mathrm{4}} \right)\left({a}−{x}_{\mathrm{4}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\left({a}+\frac{\mathrm{1}}{{t}_{\mathrm{4}} }\right)\left({a}−{t}_{\mathrm{4}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\left({a}+\frac{\mathrm{2}}{{a}−\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}\right)\left({a}+\frac{{a}−\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\right) \\ $$$${F}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left({a}+{y}_{\mathrm{3}} \right)\left({a}−{x}_{\mathrm{3}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\left({a}+\frac{\mathrm{1}}{{t}_{\mathrm{3}} }\right)\left({a}−{t}_{\mathrm{3}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\left({a}+\frac{\mathrm{2}}{{a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}\right)\left({a}+\frac{{a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\right) \\ $$$${F}_{\mathrm{3}} =\int_{{x}_{\mathrm{4}} \:} ^{{x}_{\mathrm{3}} } \frac{\mathrm{1}}{{x}}{dx}=\left(\mathrm{ln}\:\mid{x}\mid\right)\mid_{{t}_{\mathrm{4}} } ^{{t}_{\mathrm{3}} } =\mathrm{ln}\:\mid\frac{{t}_{\mathrm{3}} }{{t}_{\mathrm{4}} }\mid=\mathrm{ln}\:\mid\frac{{a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{{a}−\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}\mid \\ $$$$ \\ $$$${F}=\frac{\mathrm{1}}{\mathrm{2}}\left({a}+\frac{\mathrm{2}}{{a}−\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}\right)\left({a}+\frac{{a}−\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left({a}+\frac{\mathrm{2}}{{a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}\right)\left({a}+\frac{{a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\right)−\mathrm{ln}\:\mid\frac{{a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{{a}−\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}\mid \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com