Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 102260 by ajfour last updated on 07/Jul/20

Commented by ajfour last updated on 07/Jul/20

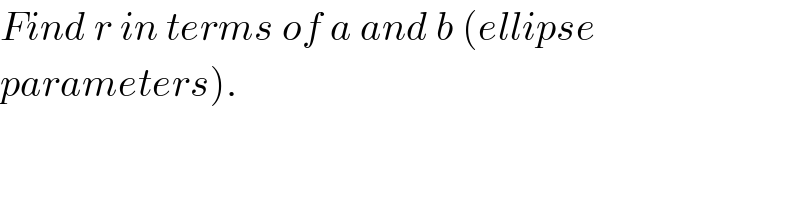
Find r in terms of a and b (ellipse parameters).

$${Find}\:{r}\:{in}\:{terms}\:{of}\:{a}\:{and}\:{b}\:\left({ellipse}\right. \\ $$$$\left.{parameters}\right). \\ $$

Commented by mr W last updated on 07/Jul/20

won′t be easy sir...

$${won}'{t}\:{be}\:{easy}\:{sir}... \\ $$

Answered by mr W last updated on 07/Jul/20

μ=(b/a) touching point P(a cos θ, b sin θ) tan ϕ=y′=(dy/dθ)×(1/(dx/dθ))=−((b cos θ)/(a sin θ))=−(μ/(tan θ)) tan φ=−(1/(tan ϕ))=((tan θ)/μ) center of circle 1 (r, h) r=a cos θ_1 +r cos φ_1 ⇒r=a(1/(√(1+tan^2 θ_1 )))+r(μ/(√(μ^2 +tan^2 θ_1 ))) ⇒(1/(√(1+tan^2 θ_1 )))=(r/a)(1−(μ/(√(μ^2 +tan^2 θ_1 )))) ⇒(1/(√(1+tan^2 θ_1 )))=ξ(1−(μ/(√(μ^2 +tan^2 θ_1 )))) ⇒tan θ_1 =f_1 (ξ) ... h=b sin θ_1 +r sin φ_1 ⇒(h/a)=μ sin θ_1 +ξ((tan θ_1 )/(√(μ^2 +tan^2 θ_1 ))) ⇒(h/a)=((μ tan θ_1 )/(√(1+tan^2 θ_1 )))+((ξ tan θ_1 )/(√(μ^2 +tan^2 θ_1 ))) center of circle 1 (k, r) ⇒r=b sin θ_2 +r((tan θ_2 )/(√(μ^2 +tan^2 θ_2 ))) ⇒(μ/(√(1+tan^2 θ_2 )))=ξ((1/(tan θ_2 ))−(1/(√(μ^2 +tan^2 θ_2 )))) ⇒tan θ_2 =f_2 (ξ) ... ⇒k=a cos θ_2 +r(μ/(√(μ^2 +tan^2 θ_2 ))) ⇒(k/a)=(1/(√(1+tan^2 θ_2 )))+((μξ)/(√(μ^2 +tan^2 θ_2 ))) (k−r)^2 +(r−h)^2 =(2r)^2 ((k/a)−ξ)^2 +((h/a)−ξ)^2 =4ξ^2 ((1/(√(1+tan^2 θ_2 )))+((μξ)/(√(μ^2 +tan^2 θ_2 )))−ξ)^2 +(((μ tan θ_1 )/(√(1+tan^2 θ_1 )))+((ξ tan θ_1 )/(√(μ^2 +tan^2 θ_1 )))−ξ)^2 =4ξ^2 ⇒ξ=(r/a)=...

$$\mu=\frac{{b}}{{a}} \\ $$$${touching}\:{point}\:{P}\left({a}\:\mathrm{cos}\:\theta,\:{b}\:\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{tan}\:\varphi={y}'=\frac{{dy}}{{d}\theta}×\frac{\mathrm{1}}{\frac{{dx}}{{d}\theta}}=−\frac{{b}\:\mathrm{cos}\:\theta}{{a}\:\mathrm{sin}\:\theta}=−\frac{\mu}{\mathrm{tan}\:\theta} \\ $$$$\mathrm{tan}\:\phi=−\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}=\frac{\mathrm{tan}\:\theta}{\mu} \\ $$$$ \\ $$$${center}\:{of}\:{circle}\:\mathrm{1}\:\left({r},\:{h}\right) \\ $$$${r}={a}\:\mathrm{cos}\:\theta_{\mathrm{1}} +{r}\:\mathrm{cos}\:\phi_{\mathrm{1}} \\ $$$$\Rightarrow{r}={a}\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{1}} }}+{r}\frac{\mu}{\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{1}} }} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{1}} }}=\frac{{r}}{{a}}\left(\mathrm{1}−\frac{\mu}{\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{1}} }}\right) \\ $$$$\Rightarrow\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{1}} }}=\xi\left(\mathrm{1}−\frac{\mu}{\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{1}} }}\right) \\ $$$$\Rightarrow\mathrm{tan}\:\theta_{\mathrm{1}} ={f}_{\mathrm{1}} \left(\xi\right)\:... \\ $$$$ \\ $$$${h}={b}\:\mathrm{sin}\:\theta_{\mathrm{1}} +{r}\:\mathrm{sin}\:\phi_{\mathrm{1}} \\ $$$$\Rightarrow\frac{{h}}{{a}}=\mu\:\mathrm{sin}\:\theta_{\mathrm{1}} +\xi\frac{\mathrm{tan}\:\theta_{\mathrm{1}} }{\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{1}} }} \\ $$$$\Rightarrow\frac{{h}}{{a}}=\frac{\mu\:\mathrm{tan}\:\theta_{\mathrm{1}} }{\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{1}} }}+\frac{\xi\:\mathrm{tan}\:\theta_{\mathrm{1}} }{\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{1}} }} \\ $$$$ \\ $$$${center}\:{of}\:{circle}\:\mathrm{1}\:\left({k},\:{r}\right) \\ $$$$\Rightarrow{r}={b}\:\mathrm{sin}\:\theta_{\mathrm{2}} +{r}\frac{\mathrm{tan}\:\theta_{\mathrm{2}} }{\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{2}} }} \\ $$$$\Rightarrow\frac{\mu}{\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{2}} }}=\xi\left(\frac{\mathrm{1}}{\mathrm{tan}\:\theta_{\mathrm{2}} }−\frac{\mathrm{1}}{\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{2}} }}\right) \\ $$$$\Rightarrow\mathrm{tan}\:\theta_{\mathrm{2}} ={f}_{\mathrm{2}} \left(\xi\right)\:... \\ $$$$ \\ $$$$\Rightarrow{k}={a}\:\mathrm{cos}\:\theta_{\mathrm{2}} +{r}\frac{\mu}{\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{2}} }} \\ $$$$\Rightarrow\frac{{k}}{{a}}=\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{2}} }}+\frac{\mu\xi}{\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{2}} }} \\ $$$$ \\ $$$$\left({k}−{r}\right)^{\mathrm{2}} +\left({r}−{h}\right)^{\mathrm{2}} =\left(\mathrm{2}{r}\right)^{\mathrm{2}} \\ $$$$\left(\frac{{k}}{{a}}−\xi\right)^{\mathrm{2}} +\left(\frac{{h}}{{a}}−\xi\right)^{\mathrm{2}} =\mathrm{4}\xi^{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{2}} }}+\frac{\mu\xi}{\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{2}} }}−\xi\right)^{\mathrm{2}} +\left(\frac{\mu\:\mathrm{tan}\:\theta_{\mathrm{1}} }{\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{1}} }}+\frac{\xi\:\mathrm{tan}\:\theta_{\mathrm{1}} }{\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{1}} }}−\xi\right)^{\mathrm{2}} =\mathrm{4}\xi^{\mathrm{2}} \\ $$$$\Rightarrow\xi=\frac{{r}}{{a}}=... \\ $$

Commented by ajfour last updated on 10/Jul/20

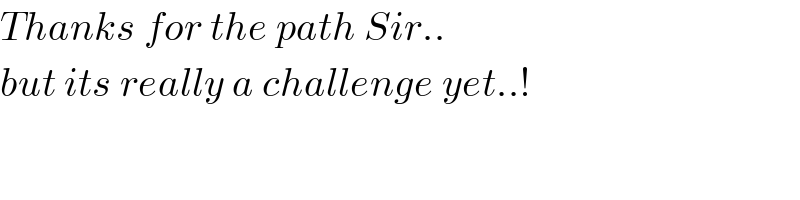
Thanks for the path Sir.. but its really a challenge yet..!

$${Thanks}\:{for}\:{the}\:{path}\:{Sir}.. \\ $$$${but}\:{its}\:{really}\:{a}\:{challenge}\:{yet}..! \\ $$

Answered by ajfour last updated on 08/Jul/20

x=acos θ , y=bsin θ −(dx/dy)=((a/b))((sin θ)/(cos θ)) = (a/b)tan θ=((am)/b) = s m =p, q for circle A and circle B. let center of right circle A be (h,r) and that of upper circle B be (r,k). h=acos θ_1 +(r/(√(s^2 +1))) = (a/(√(p^2 +1)))+(r/((((a^2 p^2 )/b^2 )+1))^(1/) ) r=((ap)/(√(p^2 +1)))+((r(((ap)/b)))/((((a^2 p^2 )/b^2 )+1))^(1/) ) similarly r=(a/(√(q^2 +1)))+(r/((((a^2 q^2 )/b^2 )+1))^(1/) ) k=((aq)/(√(q^2 +1)))+((r(((aq)/b)))/((((a^2 q^2 )/b^2 )+1))^(1/) ) Now (h−r)^2 +(k−r)^2 =4r^2 ..........

$${x}={a}\mathrm{cos}\:\theta\:,\:{y}={b}\mathrm{sin}\:\theta \\ $$$$−\frac{{dx}}{{dy}}=\left(\frac{{a}}{{b}}\right)\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}\:\:=\:\frac{{a}}{{b}}\mathrm{tan}\:\theta=\frac{{am}}{{b}}\:=\:{s} \\ $$$${m}\:={p},\:{q}\:\:\:\:{for}\:{circle}\:{A}\:{and}\:{circle}\:{B}. \\ $$$${let}\:{center}\:{of}\:{right}\:{circle}\:{A}\:{be}\:\left({h},{r}\right) \\ $$$${and}\:{that}\:{of}\:{upper}\:{circle}\:{B}\:{be}\:\left({r},{k}\right). \\ $$$$\:\:\:\:{h}={a}\mathrm{cos}\:\theta_{\mathrm{1}} +\frac{{r}}{\sqrt{{s}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\:\:\:\:\:\:=\:\frac{{a}}{\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}}+\frac{{r}}{\sqrt[{}]{\frac{{a}^{\mathrm{2}} {p}^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\mathrm{1}}} \\ $$$$\:\:\:\:\:{r}=\frac{{ap}}{\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}}+\frac{{r}\left(\frac{{ap}}{{b}}\right)}{\sqrt[{}]{\frac{{a}^{\mathrm{2}} {p}^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\mathrm{1}}} \\ $$$${similarly} \\ $$$$\:\:\:\:\:\:{r}=\frac{{a}}{\sqrt{{q}^{\mathrm{2}} +\mathrm{1}}}+\frac{{r}}{\sqrt[{}]{\frac{{a}^{\mathrm{2}} {q}^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\mathrm{1}}} \\ $$$$\:\:\:\:\:{k}=\frac{{aq}}{\sqrt{{q}^{\mathrm{2}} +\mathrm{1}}}+\frac{{r}\left(\frac{{aq}}{{b}}\right)}{\sqrt[{}]{\frac{{a}^{\mathrm{2}} {q}^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\mathrm{1}}} \\ $$$${Now}\:\:\:\left({h}−{r}\right)^{\mathrm{2}} +\left({k}−{r}\right)^{\mathrm{2}} =\mathrm{4}{r}^{\mathrm{2}} \\ $$$$.......... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com