Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 102716 by Ar Brandon last updated on 10/Jul/20

$${\mathrm{y}}^{″}+{3\mathrm{y}}^{\prime }-10\mathrm{y}={14\mathrm{e}}^{-5\mathrm{x}}$$

Answered by bramlex last updated on 10/Jul/20

$$\mathrm{Homogenous}$$$${\mathrm{r}}^2+3\mathrm{r}-10=0\Rightarrow (\mathrm{r}+5)(\mathrm{r}-2)=0$$$${\mathrm{y}}_{\mathrm{h}}={\mathrm{Ae}}^{2\mathrm{x}}+{\mathrm{Be}}^{-5\mathrm{x}}$$$$\mathrm{PI}.{\mathrm{y}}_{\mathrm{p}}={\mathrm{Cxe}}^{-5\mathrm{x}};{\mathrm{y}}^{\prime }={\mathrm{Ce}}^{-5\mathrm{x}}-{5\mathrm{Cxe}}^{-5\mathrm{x}}$$$${\mathrm{y}}^{″}=-{5\mathrm{Ce}}^{-5\mathrm{x}}-5\mathrm{C}({\mathrm{e}}^{-5\mathrm{x}}-{5\mathrm{xe}}^{-5\mathrm{x}})$$$${\mathrm{y}}^{″}=-{10\mathrm{Ce}}^{-5\mathrm{x}}+{25\mathrm{Cxe}}^{-5\mathrm{x}}$$$$\mathrm{comparing}\mathrm{coefficient}$$$$-{10\mathrm{Ce}}^{-5\mathrm{x}}+{25\mathrm{Cxe}}^{-5\mathrm{x}}+{3\mathrm{Ce}}^{-5\mathrm{x}}-{15\mathrm{Cxe}}^{-5\mathrm{x}}-{10\mathrm{Cxe}}^{-5\mathrm{x}}={14\mathrm{e}}^{-5\mathrm{x}}$$$$\Rightarrow -{7\mathrm{Ce}}^{-5\mathrm{x}}={14\mathrm{e}}^{-5\mathrm{x}}\Rightarrow \mathrm{C}=-2$$$${\mathrm{y}}_{\mathrm{p}}=-{2\mathrm{xe}}^{-5\mathrm{x}}$$$$\therefore \mathrm{generall}\mathrm{solution}$$$$\mathrm{y}={\mathrm{Ae}}^{2\mathrm{x}}+{\mathrm{Be}}^{-5\mathrm{x}}-{2\mathrm{xe}}^{-5\mathrm{x}}$$$$\stackrel{°⌢\bullet ⌢}{\text{blacktrinagledown}}$$

Commented by Ar Brandon last updated on 10/Jul/20

�� Thanks

Commented by bramlex last updated on 10/Jul/20

$$\mathrm{because}{\mathrm{e}}^{-5\mathrm{x}}\mathrm{is}\mathrm{homogenous}$$$$\mathrm{solution}$$

Commented by Ar Brandon last updated on 10/Jul/20

$$\mathrm{I}\mathrm{spent}\mathrm{my}\mathrm{time}\mathrm{trying}\mathrm{to}\mathrm{have}\mathrm{the}\mathrm{solution}\mathrm{using}$$$${\mathrm{y}}_{\mathrm{p}}=\lambda {\mathrm{e}}^{-5\mathrm{x}}$$$$\mathrm{But}\mathrm{why}\mathrm{is}\mathrm{it}\mathrm{instead}{\mathrm{y}}_{\mathrm{p}}={\mathrm{Cxe}}^{-5\mathrm{x}}?$$

Commented by Ar Brandon last updated on 10/Jul/20

$$\mathrm{And}...\mathrm{how}\mathrm{does}\mathrm{that}\mathrm{affect}\mathrm{your}\mathrm{choice}\mathrm{of}{\mathrm{y}}_{\mathrm{p}}?$$

Commented by Ar Brandon last updated on 10/Jul/20

$$\mathrm{OK}\mathrm{I}\mathrm{think}{\mathrm{I}}^{\prime }\mathrm{ve}\mathrm{understood}.\mathrm{I}\mathrm{completely}\mathrm{forgot}$$$$\mathrm{about}\mathrm{that}.\mathrm{The}\mathrm{form}\lambda {\mathrm{e}}^{-5\mathrm{x}}\mathrm{is}\mathrm{already}\mathrm{present}\mathrm{in}$$$$\mathrm{the}\mathrm{Complementary}\mathrm{function}\mathrm{and}{\mathrm{it}}^{\prime }\mathrm{s}\mathrm{pointless}\mathrm{having}$$$$\mathrm{it}\mathrm{again}\mathrm{in}{\mathrm{y}}_{\mathrm{p}}.\mathrm{So}\mathrm{we}\mathrm{therefore}\mathrm{move}\mathrm{to}\mathrm{the}\mathrm{higher}$$$$\mathrm{degree}\mathrm{of}\mathrm{x}.$$

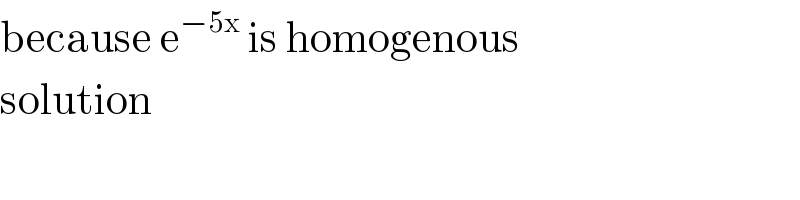
Commented by Ar Brandon last updated on 10/Jul/20

�� Thanks

Commented by Ar Brandon last updated on 10/Jul/20

https://www.pdfdrive.com/search?q=jee+mathematics&pagecount=&pubyear=&searchin=

Commented by Dwaipayan Shikari last updated on 10/Jul/20

$$DoyoustudyIndianIITJEEmathbooksir?$$

Commented by Ar Brandon last updated on 10/Jul/20

Yes bro,�� They're among my ebooks.��

Commented by Dwaipayan Shikari last updated on 10/Jul/20

Oh I am a Indian student also����.Which book do you study?��

Commented by Ar Brandon last updated on 10/Jul/20

��From your name I could deduce that.

Commented by Ar Brandon last updated on 10/Jul/20

But actually I just use these JEE Ebooks to help maximise my skills. I noticed it contains questions which push you to the peak of reasoning in every chapter.And I'm also a student.��

Commented by Dwaipayan Shikari last updated on 10/Jul/20

�� I am also.......( understand what I want to mean)

Commented by Ar Brandon last updated on 10/Jul/20

����

Commented by IRAN_majid last updated on 10/Jul/20

$$ok$$

Answered by mathmax by abdo last updated on 10/Jul/20

$$\mathrm{wronskien}\mathrm{method}$$$$\mathrm{he}\to {\mathrm{y}}^{{}^{″}}+{3\mathrm{y}}^{{}^{\prime }}-10\mathrm{y}=0\Rightarrow {\mathrm{r}}^2+3\mathrm{r}-10=0$$$$\mathrm{\Delta }=9-4(-10)=49\Rightarrow {\mathrm{r}}_1=\frac{-3+7}{2}=2\mathrm{and}{\mathrm{r}}_2=\frac{-3-7}{2}=-5\Rightarrow$$$$\Rightarrow {\mathrm{y}}_{\mathrm{h}}=\mathrm{a}{\mathrm{e}}^{2\mathrm{x}}+\mathrm{b}{\mathrm{e}}^{-5\mathrm{x}}={\mathrm{au}}_1+{\mathrm{bu}}_2$$$$\mathrm{w}({\mathrm{u}}_1,{\mathrm{u}}_2)=\left|\begin{array}{c}{\mathrm{e}}^{2\mathrm{x}}{\mathrm{e}}^{-5\mathrm{x}}\\ {2\mathrm{e}}^{2\mathrm{x}}-5{\mathrm{e}}^{-5\mathrm{x}}\end{array}\right|=-5{\mathrm{e}}^{-3\mathrm{x}}-{2\mathrm{e}}^{-3\mathrm{x}}=-7{\mathrm{e}}^{-3\mathrm{x}}$$$${\mathrm{W}}_1=\left|\begin{array}{c}0{\mathrm{e}}^{-5\mathrm{x}}\\ 14{\mathrm{e}}^{-5\mathrm{x}}-{5\mathrm{e}}^{-5\mathrm{x}}\end{array}\right|=-14{\mathrm{e}}^{-10\mathrm{x}}$$$${\mathrm{W}}_2=\left|\begin{array}{c}{\mathrm{e}}^{2\mathrm{x}}0\\ {2\mathrm{e}}^{2\mathrm{x}}14{\mathrm{e}}^{-5\mathrm{x}}\end{array}\right|={14\mathrm{e}}^{-3\mathrm{x}}$$$${\mathrm{v}}_1=\int \frac{{\mathrm{w}}_1}{\mathrm{W}}\mathrm{dx}=\int \frac{-14{\mathrm{e}}^{-10\mathrm{x}}}{-7{\mathrm{e}}^{-3\mathrm{x}}}\mathrm{dx}=2\int {\mathrm{e}}^{-7\mathrm{x}}\mathrm{dx}=-\frac{2}{7}{\mathrm{e}}^{-7\mathrm{x}}$$$${\mathrm{v}}_2=\int \frac{{\mathrm{W}}_2}{\mathrm{W}}\mathrm{dx}=\int \frac{{14\mathrm{e}}^{-3\mathrm{x}}}{-{7\mathrm{e}}^{-3\mathrm{x}}}\mathrm{dx}=-2\mathrm{x}\Rightarrow {\mathrm{y}}_{\mathrm{p}}={\mathrm{u}}_1{\mathrm{v}}_1+{\mathrm{u}}_2{\mathrm{v}}_2$$$$={\mathrm{e}}^{2\mathrm{x}}\times (-\frac{2}{7}){\mathrm{e}}^{-7\mathrm{x}}+{\mathrm{e}}^{-5\mathrm{x}}\times (-2\mathrm{x})=-\frac{2}{7}{\mathrm{e}}^{-7\mathrm{x}}-2\mathrm{x}{\mathrm{e}}^{-5\mathrm{x}}\Rightarrow$$$$\mathrm{the}\mathrm{general}\mathrm{solution}\mathrm{is}\mathrm{y}={\mathrm{y}}_{\mathrm{h}}+{\mathrm{y}}_{\mathrm{p}}$$$$\mathrm{y}={\mathrm{ae}}^{2\mathrm{x}}+\mathrm{b}{\mathrm{e}}^{-5\mathrm{x}}-\frac{2}{7}{\mathrm{e}}^{-7\mathrm{x}}-2\mathrm{x}{\mathrm{e}}^{-5\mathrm{x}}$$$$$$

Commented by Ar Brandon last updated on 10/Jul/20

What's the theory, Sir ? ��

Commented by Ar Brandon last updated on 10/Jul/20

I understand you may be so busy by now. Please reply whenever you feel it's OK to do so.��

Commented by mathmax by abdo last updated on 10/Jul/20

$$\mathrm{wronskien}\mathrm{method}$$

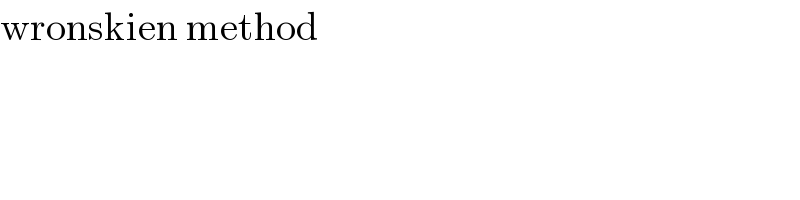
Answered by Aziztisffola last updated on 10/Jul/20

Terms of Service

Privacy Policy

Contact: info@tinkutara.com