Question Number 102816 by mr W last updated on 11/Jul/20

How many 6 digit numbers exist whose digits have exactly the sum 13? for example 120505 is such a number.

Commented byRasheed.Sindhi last updated on 11/Jul/20

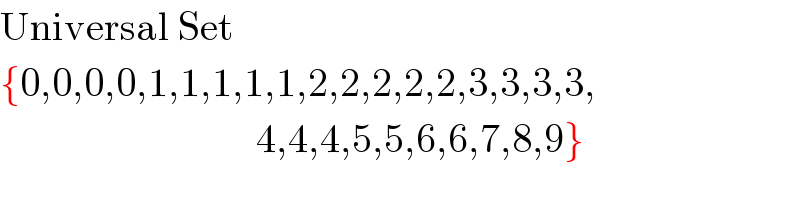
Universal Set {0,0,0,0,1,1,1,1,1,2,2,2,2,2,3,3,3,3, 4,4,4,5,5,6,6,7,8,9}

Commented byaurpeyz last updated on 11/Jul/20

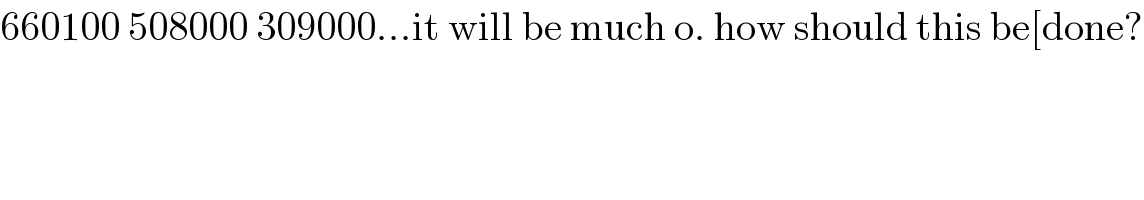
660100 508000 309000...it will be much o. how should this be[done?

Commented bymr W last updated on 11/Jul/20

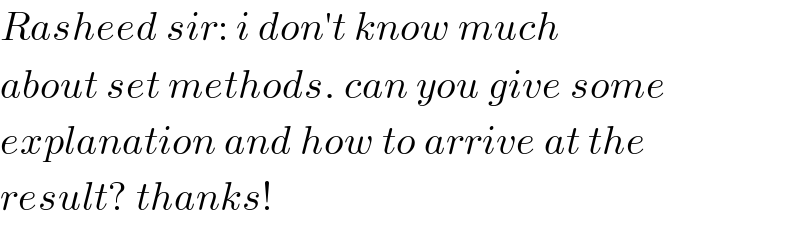
Rasheed sir: i don′t know much about set methods. can you give some explanation and how to arrive at the result? thanks!

Commented bymr W last updated on 11/Jul/20

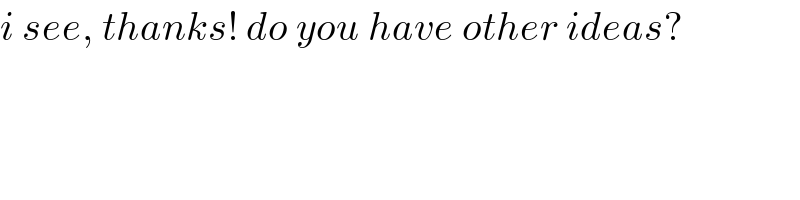
i see, thanks! do you have other ideas?

Commented byRasheed.Sindhi last updated on 11/Jul/20

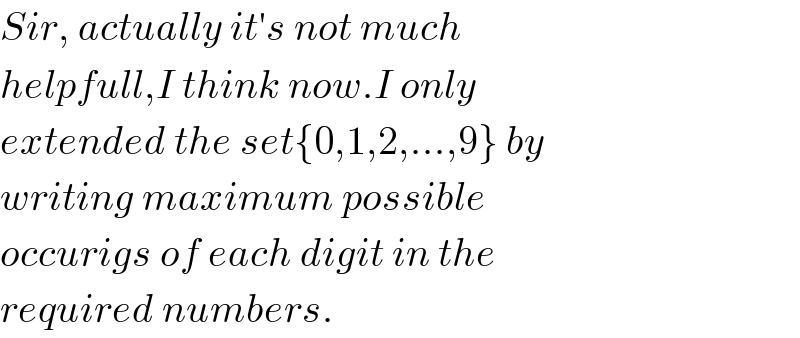
Sir, actually it′s not much helpfull,I think now.I only extended the set{0,1,2,...,9} by writing maximum possible occurigs of each digit in the required numbers.

Commented bymr W last updated on 11/Jul/20

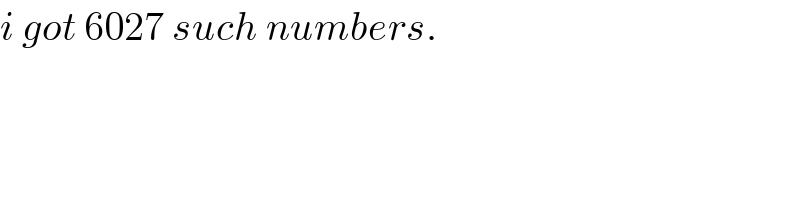
i got 6027 such numbers.

Commented byRasheed.Sindhi last updated on 11/Jul/20

Sir I thought to attack the problem as follows: (i) To determine the number of partions(in an order) of 13 using above ′universal set′ {0,0,0,0,1,1,1,1,1,2,2,2,2,2,3,3,3,3, 4,4,4,5,5,6,6,7,8,9} (ii)To determine number of ′permutations′ of each partitions. (iii)After than number of excluding unwanted numbers. I am not confident of these ideas.You can do better.

Commented byprakash jain last updated on 11/Jul/20

This method i think is known as generating function method, used in problem involving coins etc.

Commented byprakash jain last updated on 11/Jul/20

Thanks. I will recheck calculation for both methods.

Commented byPRITHWISH SEN 2 last updated on 11/Jul/20

Sir itis really hard . But I might find a different way. For instance let find the 3 digits numbers in between 100 and 200 whose digit sum is 12 Sum of digits Numbers 1 −−−−100 2−−−−101−−−−110 3−−−−102−−−−111−−−−120 4−−−−103−−−−112−−−−121−−−−130 5−−−−104−−−−113−−−−122−−−−131 6−−−−105−−−−114−−−−123−−−−132 7−−−−106−−−−115−−−−124−−−−133 8−−−−107−−−−116−−−−125−−−−134 9−−−−108−−−−117−−−−126−−−−135 10−−− 109−−−−118−−−− 127−−−−136 11−−−−−−−−−119−−−−128−−−−137 12−−−−−−−−−−−−−−−129−−−−138 and so on.. so the first number is 129 and the last number is 129+9×n<200 n=7 ∴ no. of 3 digits number whose sum is 12 is = 7+1=8 sir is it can be helpful for such problems ? Sir Rasheed and Mr.Wsir please share your comments.

Commented bymr W last updated on 11/Jul/20

yes! this is the best method to solve. please recheck your formula, i think it contains an error. i got: C_5 ^(17) −C_5 ^8 −5C_5 ^7 =6027

Commented bymr W last updated on 11/Jul/20

big thanks to all for the many ideas!

Commented byprakash jain last updated on 11/Jul/20

See Q22040

Commented byprakash jain last updated on 11/Jul/20

Q55502

Commented byprakash jain last updated on 11/Jul/20

Several other questions answered by mr W only using method. mr W, is the same method not applicable here. I did remember some previous questions so searched.

Commented byPRITHWISH SEN 2 last updated on 11/Jul/20

Thank you sirs

Commented bymr W last updated on 11/Jul/20

there is no standard way for such problems. the way you are trying can reach the goal, but it could be tough.

Commented byRasheed.Sindhi last updated on 11/Jul/20

Sir an idea comes to me! If sum of digits is 13 that means numbers which leaves remainder 1 when they′re divided by 3. That is 3k+1 type numbers. The numbers leaves remainder 4 when they′re divided by 9. That is the numbers of 9k+4 types....Some extra numbers ....

Commented byPRITHWISH SEN 2 last updated on 11/Jul/20

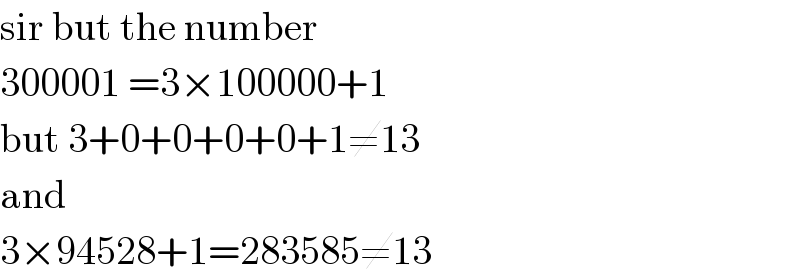
sir but the number 300001 =3×100000+1 but 3+0+0+0+0+1≠13 and 3×94528+1=283585≠13

Commented byRasheed.Sindhi last updated on 11/Jul/20

Hello sir PRITHWISH SEN! You′re right sir! Some extra numbers will also included.So...

Commented byPRITHWISH SEN 2 last updated on 11/Jul/20

Please check this 1^(st) Digit No. of numbers 9 The coefficient of 4 in (a^0 +a^1 +a^2 +a^3 +a^4 +a^5 +a^6 +a^7 +a^8 +a^9 )^5 8 The coeffi. of 5 in (a^0 +a^1 +a^2 +a^3 +a^4 +a^5 +a^6 +a^7 +a^8 +a^9 )^5 7 The coeffi. of 6 in (a^0 +a^1 +a^2 +a^3 +a^4 +a^5 +a^6 +a^7 +a^8 +a^9 )^5 6 The coeffi. of 7 in (a^0 +a^1 +a^2 +a^3 +a^4 +a^5 +a^6 +a^7 +a^8 +a^9 )^5 5 The coeffi. of 8 in (a^0 +a^1 +a^2 +a^3 +a^4 +a^5 +a^6 +a^7 +a^8 +a^9 )^5 4 The coeffi. of 9 in (a^0 +a^1 +a^2 +a^3 +a^4 +a^5 +a^6 +a^7 +a^8 +a^9 )^5 3 The coeffi. of 10 in (a^0 +a^1 +a^2 +a^3 +a^4 +a^5 +a^6 +a^7 +a^8 +a^9 )^5 2 The coeffi. of 11 in (a^0 +a^1 +a^2 +a^3 +a^4 +a^5 +a^6 +a^7 +a^8 +a^9 )^5 1 The coeffi. of 12 in (a^0 +a^1 +a^2 +a^3 +a^4 +a^5 +a^6 +a^7 +a^8 +a^9 )^5

Commented byprakash jain last updated on 11/Jul/20

First digits 1 to 9 rest all 0 to 9 (x^1 +....+x^9 )(1+...+x^9 )^5 Digits with sum 13 is given by coefficient of x^(13) in above expression. ((x(1−x^9 ))/(1−x))×(((1−x^(10) )^5 )/((1−x)^5 )) =x(1−x^9 −x^(10) +higherpower)(1−x)^(−6) =x(1−x^9 −5x^(10) )(1+Σ_(i=1) ^∞ ^(6+i−1) C_i x^i ) =(x−x^(10) −x^(11) )(...) Terms in ()that will given x^(13 ) x^(12) ,x^3 ,x^2 ^(17) C_5 −^8 C_3 −5 ^7 C_2 (correction (1−x^(10) )^5 was earlier written (1−x^(10) +..) it should be (1−5x^(10) +..)

Commented bymr W last updated on 11/Jul/20

yes sir! i solved similar questions sometimes ago, but i can′t remember the old posts. how did you find these old posts?

Commented byprakash jain last updated on 11/Jul/20

I searched for generating or just generat etc. tried 2−3 search text.

Commented bymr W last updated on 11/Jul/20

thanks sir! in this way one can find some old posts, great!

Commented byPRITHWISH SEN 2 last updated on 11/Jul/20

sir prakash jain i think your 2^(nd) expression will be (1+....+x^9 )^5 not 6

Commented byprakash jain last updated on 11/Jul/20

yes. it is 5.

Commented byprakash jain last updated on 11/Jul/20

ok. I realize now. in previous step i have written six.

Answered by mr W last updated on 11/Jul/20

let′s look at the general case: how many n digit numbers exist whose digits have exactly the sum m? say such a number is d_1 d_2 d_3 ...d_n with the conditions: 1≤d_1 ≤9 0≤d_2 ,d_3 ,...,d_n ≤9 so the question is how many integral solutions the following equation d_1 +d_2 +d_3 +...+d_n =m ...(I) has under the given conditions. we can use the generating functions for d_1 : x+x^2 +x^3 +...+x^9 for d_2 ,d_3 ,...,d_n : 1+x+x^2 +x^3 +...+x^9 for d_1 +d_2 +d_3 +...+d_n it is then (x+x^2 +x^3 +...+x^9 )(1+x+x^2 +x^3 +...+x^9 )^(n−1) =((x(1−x^9 )(1−x^(10) )^(n−1) )/((1−x)^n )) =x(1−x^9 )(1−x^(10) )^(n−1) Σ_(k=0) ^∞ C_(n−1) ^(k+n−1) x^k =x(1−x^9 )[Σ_(r=0) ^(n−1) (−1)^r C_r ^(n−1) x^(10r) ][Σ_(k=0) ^∞ C_(n−1) ^(k+n−1) x^k ] the coefficient of the x^m term in this generating function represents the number of solutions of eqn. (I). example: n=6, m=13 GF=x(1−x^9 )(1−5x^(10) +...)Σ_(k=0) ^∞ C_5 ^(k+5) x^k =x(1−x^9 −5x^(10) +...)Σ_(k=0) ^∞ C_5 ^(k+5) x^k coefficient of x^(13) term is (for k=12, 3, 2) C_5 ^(17) −C_5 ^8 −5C_5 ^7 =6027

Commented byPRITHWISH SEN 2 last updated on 11/Jul/20

Thanks sir

Answered by prakash jain last updated on 11/Jul/20

xxxxxxxxxxxxxxxxxx (18x) Replace any 5 of last 17 x by a bar count the number of xs between to bars to get a digit. Now this will include cases where where all 5 bars are included in 8 or less continous xs. Meaning digits has to be ≤9. # of ways to place 5 bars= ^(17) C_5 one digits is 10=6× ^5 C_3 + ^7 C_4 + ^6 C_4 =110 one digits is 11=5× ^4 C_3 + ^6 C_4 + ^5 C_4 =55 one digits is 12=4× ^3 C_3 + ^5 C_4 +^4 C_4 =10 one digits is 13=1 valid outcomes =^(17) C_5 −161=6188−161=6027 count the number of x between 2 bars to get the digit. x∣10x∣5x to x6x∣10x xx∣xxx∣xxx∣∣xxx∣xx 233032 xx∣∣∣∣∣∣xxxxxxxxxxx

Commented byRasheed.Sindhi last updated on 11/Jul/20

Sir really useful method! I remember now that long ago I had learnt it from you but I forgot!

Commented byprakash jain last updated on 11/Jul/20

This method is commonly known as stars and bars. Very useful for dividing n items in m boxes. The above is a special cases where first box is not empty and other boxes can be empty but cannot contain more than 9 items.