Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 102836 by ajfour last updated on 11/Jul/20

Commented by ajfour last updated on 11/Jul/20

△ABC is equilateral with side a. If regions 1,2,3 have equal perimeters, find x/a.

$$\bigtriangleup{ABC}\:{is}\:{equilateral}\:{with}\:{side}\:{a}. \\ $$$${If}\:{regions}\:\mathrm{1},\mathrm{2},\mathrm{3}\:{have}\:{equal} \\ $$$${perimeters},\:{find}\:{x}/{a}. \\ $$

Answered by mr W last updated on 11/Jul/20

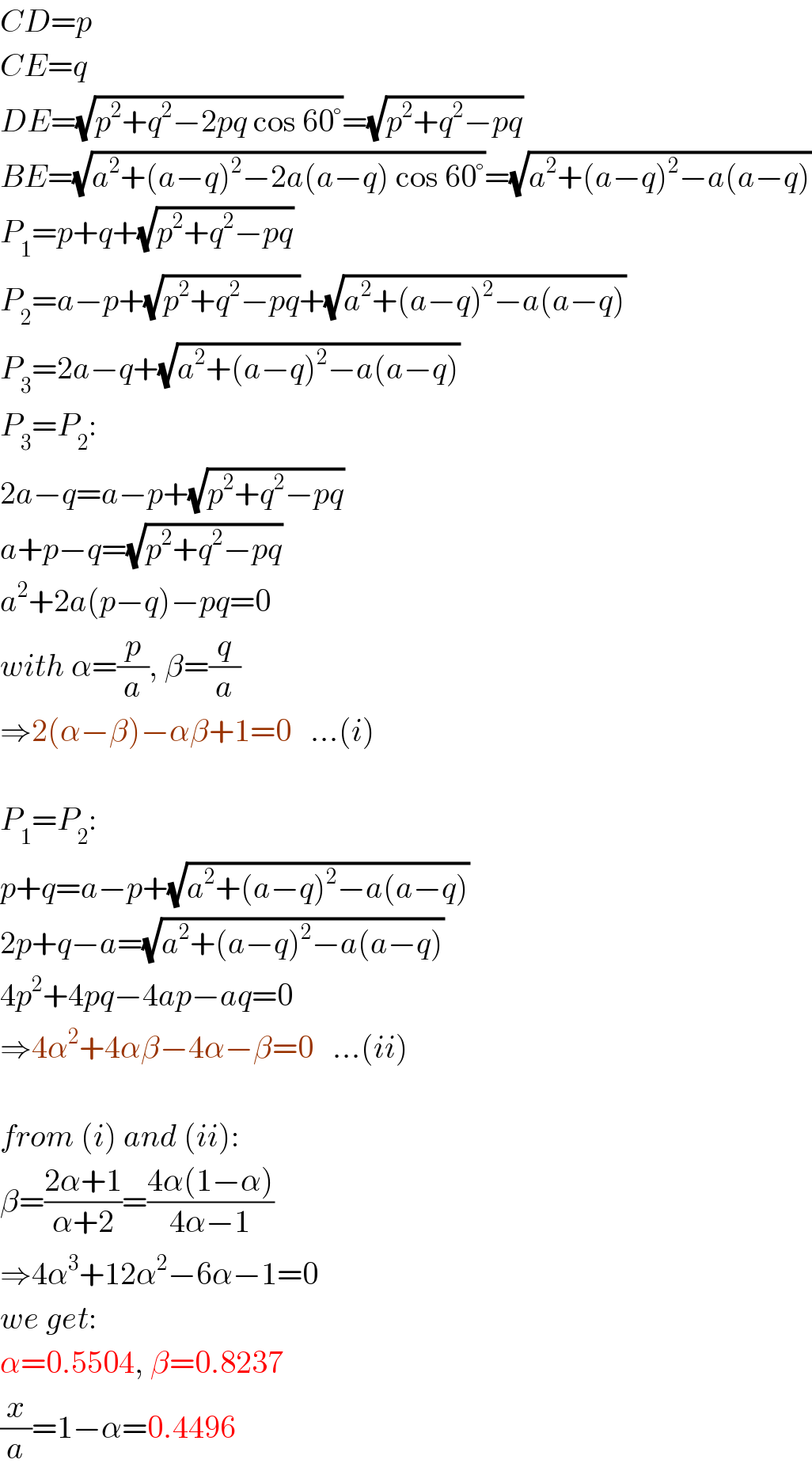
CD=p CE=q DE=(√(p^2 +q^2 −2pq cos 60°))=(√(p^2 +q^2 −pq)) BE=(√(a^2 +(a−q)^2 −2a(a−q) cos 60°))=(√(a^2 +(a−q)^2 −a(a−q))) P_1 =p+q+(√(p^2 +q^2 −pq)) P_2 =a−p+(√(p^2 +q^2 −pq))+(√(a^2 +(a−q)^2 −a(a−q))) P_3 =2a−q+(√(a^2 +(a−q)^2 −a(a−q))) P_3 =P_2 : 2a−q=a−p+(√(p^2 +q^2 −pq)) a+p−q=(√(p^2 +q^2 −pq)) a^2 +2a(p−q)−pq=0 with α=(p/a), β=(q/a) ⇒2(α−β)−αβ+1=0 ...(i) P_1 =P_2 : p+q=a−p+(√(a^2 +(a−q)^2 −a(a−q))) 2p+q−a=(√(a^2 +(a−q)^2 −a(a−q))) 4p^2 +4pq−4ap−aq=0 ⇒4α^2 +4αβ−4α−β=0 ...(ii) from (i) and (ii): β=((2α+1)/(α+2))=((4α(1−α))/(4α−1)) ⇒4α^3 +12α^2 −6α−1=0 we get: α=0.5504, β=0.8237 (x/a)=1−α=0.4496

$${CD}={p} \\ $$$${CE}={q} \\ $$$${DE}=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{2}{pq}\:\mathrm{cos}\:\mathrm{60}°}=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{pq}} \\ $$$${BE}=\sqrt{{a}^{\mathrm{2}} +\left({a}−{q}\right)^{\mathrm{2}} −\mathrm{2}{a}\left({a}−{q}\right)\:\mathrm{cos}\:\mathrm{60}°}=\sqrt{{a}^{\mathrm{2}} +\left({a}−{q}\right)^{\mathrm{2}} −{a}\left({a}−{q}\right)} \\ $$$${P}_{\mathrm{1}} ={p}+{q}+\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{pq}} \\ $$$${P}_{\mathrm{2}} ={a}−{p}+\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{pq}}+\sqrt{{a}^{\mathrm{2}} +\left({a}−{q}\right)^{\mathrm{2}} −{a}\left({a}−{q}\right)} \\ $$$${P}_{\mathrm{3}} =\mathrm{2}{a}−{q}+\sqrt{{a}^{\mathrm{2}} +\left({a}−{q}\right)^{\mathrm{2}} −{a}\left({a}−{q}\right)} \\ $$$${P}_{\mathrm{3}} ={P}_{\mathrm{2}} : \\ $$$$\mathrm{2}{a}−{q}={a}−{p}+\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{pq}} \\ $$$${a}+{p}−{q}=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{pq}} \\ $$$${a}^{\mathrm{2}} +\mathrm{2}{a}\left({p}−{q}\right)−{pq}=\mathrm{0} \\ $$$${with}\:\alpha=\frac{{p}}{{a}},\:\beta=\frac{{q}}{{a}} \\ $$$$\Rightarrow\mathrm{2}\left(\alpha−\beta\right)−\alpha\beta+\mathrm{1}=\mathrm{0}\:\:\:...\left({i}\right) \\ $$$$ \\ $$$${P}_{\mathrm{1}} ={P}_{\mathrm{2}} : \\ $$$${p}+{q}={a}−{p}+\sqrt{{a}^{\mathrm{2}} +\left({a}−{q}\right)^{\mathrm{2}} −{a}\left({a}−{q}\right)} \\ $$$$\mathrm{2}{p}+{q}−{a}=\sqrt{{a}^{\mathrm{2}} +\left({a}−{q}\right)^{\mathrm{2}} −{a}\left({a}−{q}\right)} \\ $$$$\mathrm{4}{p}^{\mathrm{2}} +\mathrm{4}{pq}−\mathrm{4}{ap}−{aq}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{4}\alpha\beta−\mathrm{4}\alpha−\beta=\mathrm{0}\:\:\:...\left({ii}\right) \\ $$$$ \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right): \\ $$$$\beta=\frac{\mathrm{2}\alpha+\mathrm{1}}{\alpha+\mathrm{2}}=\frac{\mathrm{4}\alpha\left(\mathrm{1}−\alpha\right)}{\mathrm{4}\alpha−\mathrm{1}} \\ $$$$\Rightarrow\mathrm{4}\alpha^{\mathrm{3}} +\mathrm{12}\alpha^{\mathrm{2}} −\mathrm{6}\alpha−\mathrm{1}=\mathrm{0} \\ $$$${we}\:{get}: \\ $$$$\alpha=\mathrm{0}.\mathrm{5504},\:\beta=\mathrm{0}.\mathrm{8237} \\ $$$$\frac{{x}}{{a}}=\mathrm{1}−\alpha=\mathrm{0}.\mathrm{4496} \\ $$

Commented by ajfour last updated on 11/Jul/20

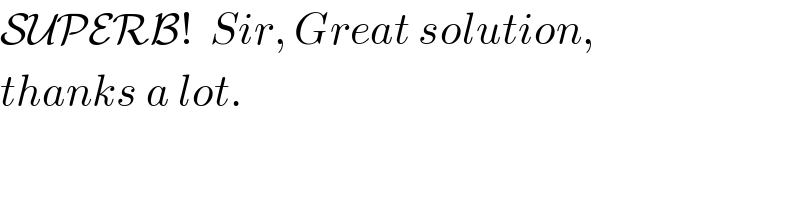
SUPERB! Sir, Great solution, thanks a lot.

$$\mathcal{SUPERB}!\:\:{Sir},\:{Great}\:{solution}, \\ $$$${thanks}\:{a}\:{lot}. \\ $$

Answered by 1549442205 last updated on 11/Jul/20

Commented by 1549442205 last updated on 12/Jul/20

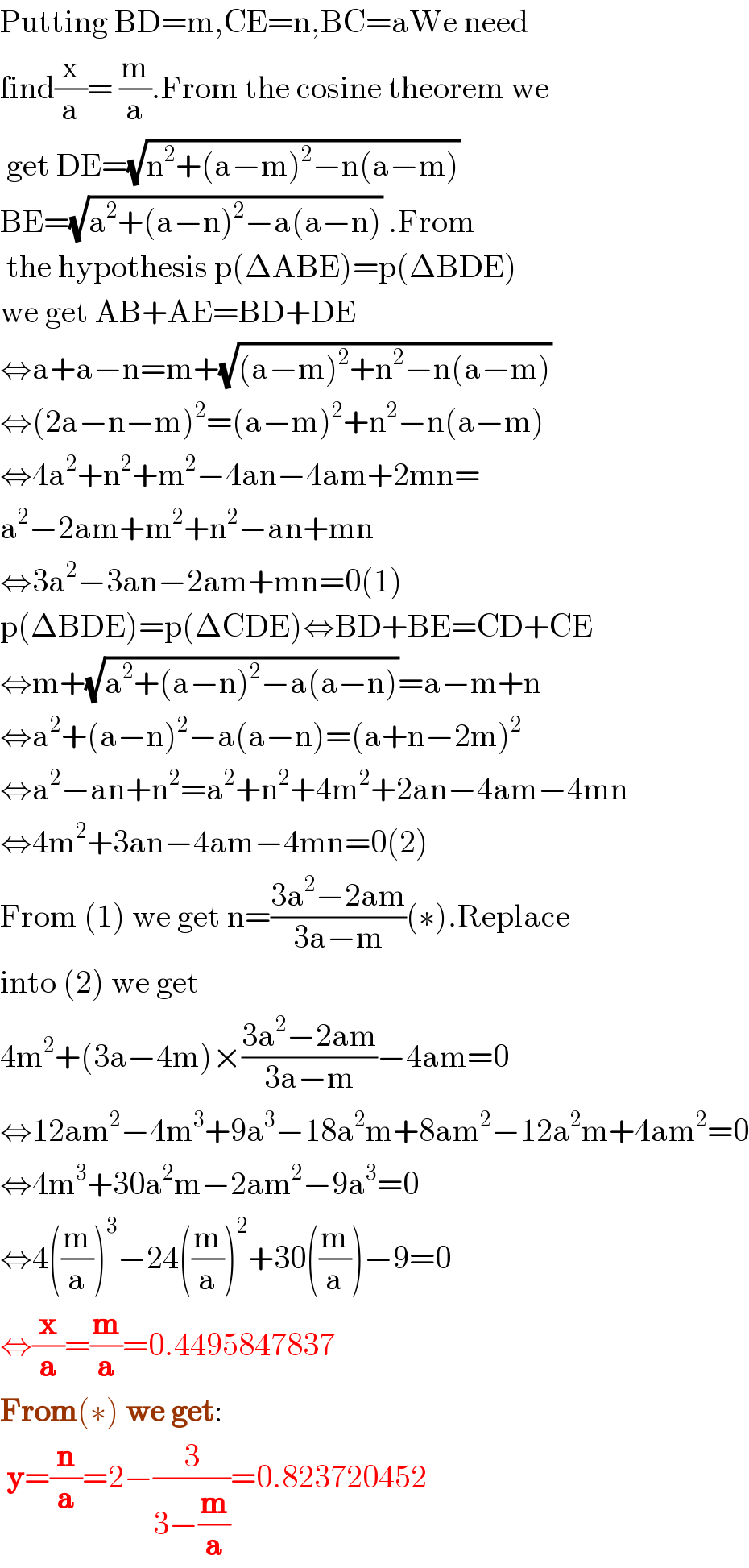
Putting BD=m,CE=n,BC=aWe need find(x/a)= (m/a).From the cosine theorem we get DE=(√(n^2 +(a−m)^2 −n(a−m))) BE=(√(a^2 +(a−n)^2 −a(a−n))) .From the hypothesis p(ΔABE)=p(ΔBDE) we get AB+AE=BD+DE ⇔a+a−n=m+(√((a−m)^2 +n^2 −n(a−m))) ⇔(2a−n−m)^2 =(a−m)^2 +n^2 −n(a−m) ⇔4a^2 +n^2 +m^2 −4an−4am+2mn= a^2 −2am+m^2 +n^2 −an+mn ⇔3a^2 −3an−2am+mn=0(1) p(ΔBDE)=p(ΔCDE)⇔BD+BE=CD+CE ⇔m+(√(a^2 +(a−n)^2 −a(a−n)))=a−m+n ⇔a^2 +(a−n)^2 −a(a−n)=(a+n−2m)^2 ⇔a^2 −an+n^2 =a^2 +n^2 +4m^2 +2an−4am−4mn ⇔4m^2 +3an−4am−4mn=0(2) From (1) we get n=((3a^2 −2am)/(3a−m))(∗).Replace into (2) we get 4m^2 +(3a−4m)×((3a^2 −2am)/(3a−m))−4am=0 ⇔12am^2 −4m^3 +9a^3 −18a^2 m+8am^2 −12a^2 m+4am^2 =0 ⇔4m^3 +30a^2 m−2am^2 −9a^3 =0 ⇔4((m/a))^3 −24((m/a))^2 +30((m/a))−9=0 ⇔(x/a)=(m/a)=0.4495847837 From(∗) we get: y=(n/a)=2−(3/(3−(m/a)))=0.823720452

$$\mathrm{Putting}\:\mathrm{BD}=\mathrm{m},\mathrm{CE}=\mathrm{n},\mathrm{BC}=\mathrm{aWe}\:\mathrm{need} \\ $$$$\mathrm{find}\frac{\mathrm{x}}{\mathrm{a}}=\:\frac{\mathrm{m}}{\mathrm{a}}.\mathrm{From}\:\mathrm{the}\:\mathrm{cosine}\:\mathrm{theorem}\:\mathrm{we} \\ $$$$\:\mathrm{get}\:\mathrm{DE}=\sqrt{\mathrm{n}^{\mathrm{2}} +\left(\mathrm{a}−\mathrm{m}\right)^{\mathrm{2}} −\mathrm{n}\left(\mathrm{a}−\mathrm{m}\right)} \\ $$$$\mathrm{BE}=\sqrt{\mathrm{a}^{\mathrm{2}} +\left(\mathrm{a}−\mathrm{n}\right)^{\mathrm{2}} −\mathrm{a}\left(\mathrm{a}−\mathrm{n}\right)}\:.\mathrm{From} \\ $$$$\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{p}\left(\Delta\mathrm{ABE}\right)=\mathrm{p}\left(\Delta\mathrm{BDE}\right) \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{AB}+\mathrm{AE}=\mathrm{BD}+\mathrm{DE} \\ $$$$\Leftrightarrow\mathrm{a}+\mathrm{a}−\mathrm{n}=\mathrm{m}+\sqrt{\left(\mathrm{a}−\mathrm{m}\right)^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} −\mathrm{n}\left(\mathrm{a}−\mathrm{m}\right)} \\ $$$$\Leftrightarrow\left(\mathrm{2a}−\mathrm{n}−\mathrm{m}\right)^{\mathrm{2}} =\left(\mathrm{a}−\mathrm{m}\right)^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} −\mathrm{n}\left(\mathrm{a}−\mathrm{m}\right) \\ $$$$\Leftrightarrow\mathrm{4a}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} +\mathrm{m}^{\mathrm{2}} −\mathrm{4an}−\mathrm{4am}+\mathrm{2mn}= \\ $$$$\mathrm{a}^{\mathrm{2}} −\mathrm{2am}+\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} −\mathrm{an}+\mathrm{mn} \\ $$$$\Leftrightarrow\mathrm{3a}^{\mathrm{2}} −\mathrm{3an}−\mathrm{2am}+\mathrm{mn}=\mathrm{0}\left(\mathrm{1}\right) \\ $$$$\mathrm{p}\left(\Delta\mathrm{BDE}\right)=\mathrm{p}\left(\Delta\mathrm{CDE}\right)\Leftrightarrow\mathrm{BD}+\mathrm{BE}=\mathrm{CD}+\mathrm{CE} \\ $$$$\Leftrightarrow\mathrm{m}+\sqrt{\mathrm{a}^{\mathrm{2}} +\left(\mathrm{a}−\mathrm{n}\right)^{\mathrm{2}} −\mathrm{a}\left(\mathrm{a}−\mathrm{n}\right)}=\mathrm{a}−\mathrm{m}+\mathrm{n} \\ $$$$\Leftrightarrow\mathrm{a}^{\mathrm{2}} +\left(\mathrm{a}−\mathrm{n}\right)^{\mathrm{2}} −\mathrm{a}\left(\mathrm{a}−\mathrm{n}\right)=\left(\mathrm{a}+\mathrm{n}−\mathrm{2m}\right)^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{a}^{\mathrm{2}} −\mathrm{an}+\mathrm{n}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} +\mathrm{4m}^{\mathrm{2}} +\mathrm{2an}−\mathrm{4am}−\mathrm{4mn} \\ $$$$\Leftrightarrow\mathrm{4m}^{\mathrm{2}} +\mathrm{3an}−\mathrm{4am}−\mathrm{4mn}=\mathrm{0}\left(\mathrm{2}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\:\mathrm{we}\:\mathrm{get}\:\mathrm{n}=\frac{\mathrm{3a}^{\mathrm{2}} −\mathrm{2am}}{\mathrm{3a}−\mathrm{m}}\left(\ast\right).\mathrm{Replace} \\ $$$$\mathrm{into}\:\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{4m}^{\mathrm{2}} +\left(\mathrm{3a}−\mathrm{4m}\right)×\frac{\mathrm{3a}^{\mathrm{2}} −\mathrm{2am}}{\mathrm{3a}−\mathrm{m}}−\mathrm{4am}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{12am}^{\mathrm{2}} −\mathrm{4m}^{\mathrm{3}} +\mathrm{9a}^{\mathrm{3}} −\mathrm{18a}^{\mathrm{2}} \mathrm{m}+\mathrm{8am}^{\mathrm{2}} −\mathrm{12a}^{\mathrm{2}} \mathrm{m}+\mathrm{4am}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{4m}^{\mathrm{3}} +\mathrm{30a}^{\mathrm{2}} \mathrm{m}−\mathrm{2am}^{\mathrm{2}} −\mathrm{9a}^{\mathrm{3}} =\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{4}\left(\frac{\mathrm{m}}{\mathrm{a}}\right)^{\mathrm{3}} −\mathrm{24}\left(\frac{\mathrm{m}}{\mathrm{a}}\right)^{\mathrm{2}} +\mathrm{30}\left(\frac{\mathrm{m}}{\mathrm{a}}\right)−\mathrm{9}=\mathrm{0} \\ $$$$\Leftrightarrow\frac{\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{a}}}=\frac{\boldsymbol{\mathrm{m}}}{\boldsymbol{\mathrm{a}}}=\mathrm{0}.\mathrm{4495847837} \\ $$$$\boldsymbol{\mathrm{From}}\left(\ast\right)\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}}: \\ $$$$\:\boldsymbol{\mathrm{y}}=\frac{\boldsymbol{\mathrm{n}}}{\boldsymbol{\mathrm{a}}}=\mathrm{2}−\frac{\mathrm{3}}{\mathrm{3}−\frac{\boldsymbol{\mathrm{m}}}{\boldsymbol{\mathrm{a}}}}=\mathrm{0}.\mathrm{823720452} \\ $$

Commented by ajfour last updated on 12/Jul/20

thanks Sir, excellent.

$${thanks}\:{Sir},\:{excellent}. \\ $$

Commented by 1549442205 last updated on 13/Jul/20

You are welcome sir.

$$\mathrm{You}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com