∫ (dθ/(2sin^2 θ−cos^2 θ)) ?


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 102926 by mohammad17 last updated on 11/Jul/20

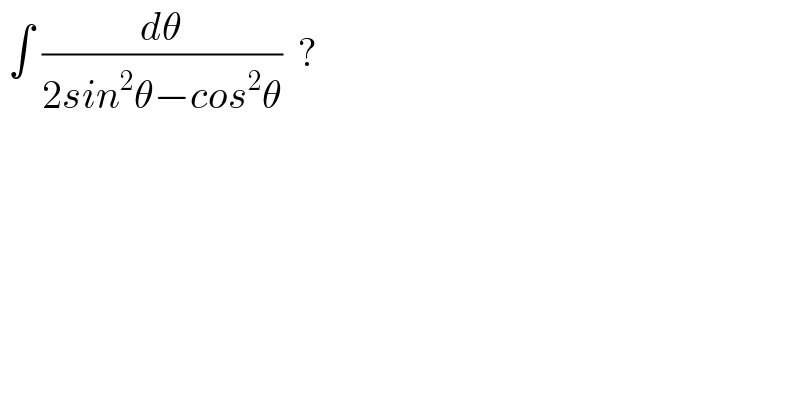
$\int \frac{d θ}{2 {s i n}^{2} θ - {c o s}^{2} θ} ?$
	Answered by OlafThorendsen last updated on 11/Jul/20

	$\int \frac{d θ}{2 \frac{2 t}{1 + t^{2}} - \frac{1 - t^{2}}{1 + t^{2}}}$ $(t = t a n \frac{θ}{2})$ $\int \frac{1 + t^{2}}{t^{2} + 4 t - 1} d θ$ $\int \frac{1 + t^{2}}{{(t + 2)}^{2} - 5} d θ$ $\int \frac{1 + t^{2}}{2 \sqrt{5}} [\frac{1}{t + 2 - \sqrt{5}} - \frac{1}{t + 2 + \sqrt{5}}] d θ$ $\frac{1}{\sqrt{5}} \ln \frac{t + 2 - \sqrt{5}}{t + 2 + \sqrt{5}} + C$ $\frac{1}{\sqrt{5}} \ln \frac{t a n \frac{θ}{2} + 2 - \sqrt{5}}{t a n \frac{θ}{2} + 2 + \sqrt{5}} + C$
	Commented by mohammad17 last updated on 11/Jul/20

	$t h a n k y o u s i r$
	Answered by Dwaipayan Shikari last updated on 11/Jul/20

	$\int \frac{{s e c}^{2} θ d θ}{2 {t a n}^{2} θ - 1} = \int \frac{d t}{2 t^{2} - 1} = \frac{1}{2} \int \frac{d t}{t^{2} - \frac{1}{2}} = \frac{1}{2 \sqrt{2}} l o g (\frac{\sqrt{2} t - 1}{\sqrt{2} t + 1}) + C (t a k e$ $t a n θ = x$ $\frac{1}{2 \sqrt{2}} l o g (\frac{\sqrt{2} t a n θ - 1}{\sqrt{2} t a n θ + 1}) + C$
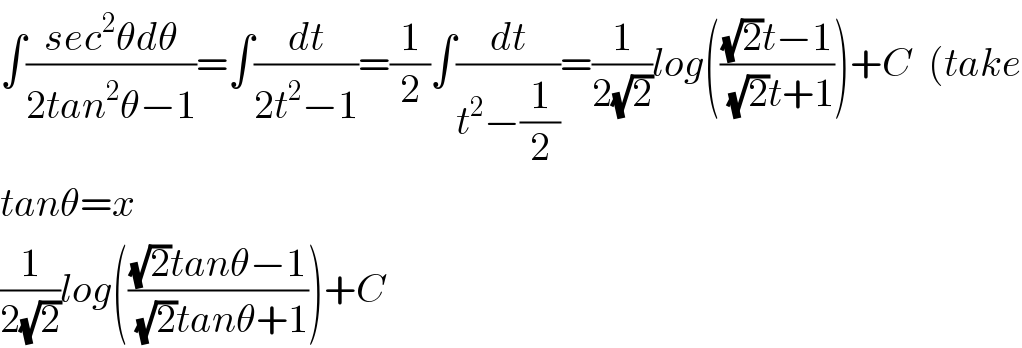
	Commented by mohammad17 last updated on 11/Jul/20

	$v e r y n i c e t h a n k y o u s i r$
	Answered by mathmax by abdo last updated on 11/Jul/20

	$I = \int \frac{dx}{{2 \sin}^{2} x - \cos^{2} x} \Rightarrow I = \int \frac{dx}{{2 \sin}^{2} x - (1 - \sin^{2} x)}$ $= \int \frac{dx}{{2 \sin}^{2} x - 1 + \sin^{2} x} = \int \frac{dx}{{3 \sin}^{2} x - 1} = \int \frac{dx}{(\sqrt{3} sinx - 1) (\sqrt{3} sinx + 1)}$ $= \frac{1}{2} \int (\frac{1}{\sqrt{3} sinx - 1} - \frac{1}{\sqrt{3} sinx + 1}) dx = H - K$ $H = \frac{1}{2} \int \frac{dx}{\sqrt{3} sinx - 1} \Rightarrow 2 H =_{\tan (\frac{x}{2}) = t} \int \frac{2 dt}{(1 + t^{2}) (\sqrt{3} \times \frac{2 t}{1 + t^{2}} - 1)}$ $= \int \frac{2 dt}{2 \sqrt{3} t - 1 - t^{2}} = - 2 \int \frac{dt}{t^{2} - 2 \sqrt{3} t + 1}$ $t^{2} - 2 \sqrt{3} t + 1 = 0 \to Δ^{^{'}} = 3 - 1 = 2 \Rightarrow t_{1} = \sqrt{3} + \sqrt{2} and t_{2} = \sqrt{3} - \sqrt{2}$ $2 H = - 2 \int \frac{dt}{(t - t_{1}) (t - t_{2})} = \frac{- 1}{\sqrt{2}} \int (\frac{1}{t - t_{1}} - \frac{1}{t - t_{2}}) dt$ $H = - \frac{1}{2 \sqrt{2}} \ln ∣ \frac{t - t_{1}}{t - t_{2}} ∣ + C = - \frac{1}{2 \sqrt{2}} \ln ∣ \frac{\tan (\frac{x}{2}) - \sqrt{3} - \sqrt{2}}{\tan (\frac{x}{2}) - \sqrt{3} + \sqrt{2}} ∣ + C$ $K = \frac{1}{2} \int \frac{dx}{\sqrt{3} sinx + 1} \Rightarrow 2 K =_{\tan (\frac{x}{2}) = t} \int \frac{2 dt}{(1 + t^{2}) (\sqrt{3} \times \frac{2 t}{1 + t^{2}} + 1)}$ $\Rightarrow K = \int \frac{dt}{2 \sqrt{3} t + 1 + t^{2}} = \int \frac{dt}{t^{2} + 2 \sqrt{3} t + 1}$ $Δ^{^{'}} = 2 \Rightarrow t_{1} = - \sqrt{3} + \sqrt{2} and t_{2} = - \sqrt{3} - \sqrt{2} \Rightarrow$ $K = \int \frac{dt}{(t - t_{1}) (t - t_{2})} = \frac{1}{2 \sqrt{2}} \int (\frac{1}{t - t_{1}} - \frac{1}{t - t_{2}}) dt$ $= \frac{1}{2 \sqrt{2}} \ln ∣ \frac{t - t_{1}}{t - t_{2}} ∣ + C = \frac{1}{2 \sqrt{2}} \ln ∣ \frac{\tan (\frac{x}{2}) + \sqrt{3} - \sqrt{2}}{\tan (\frac{x}{2}) + \sqrt{3} + \sqrt{2}} ∣ + C$ $I = H - K$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum