
Question and Answers Forum
Question Number 102985 by DGmichael last updated on 12/Jul/20
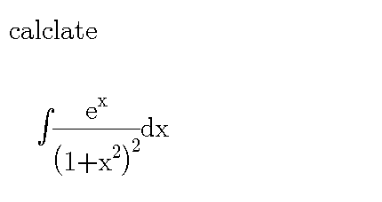
Answered by mathmax by abdo last updated on 12/Jul/20
![at form of serie let f(x) =∫_0 ^x (e^t /((1+t^2 )^2 ))dt if o≤x<1 we have (1/(1+u)) =Σ_(n=0) ^∞ (−1)^n u^(n ) ⇒by derivation we get −(1/((1+u)^2 )) =Σ_(n=1) ^∞ n(−1)^n u^(n−1) ⇒(1/((1+u)^2 )) =Σ_(n=1) ^∞ n(−1)^(n−1) u^(n−1) ⇒ (1/((1+t^2 )^2 )) =Σ_(n=1) ^∞ n(−1)^(n−1) t^(2n−2) ⇒f(x) =∫_0 ^(x ) e^t (Σ_(n=1) ^(∞ ) n(−1)^(n−1 ) t^(2n−2) )dt =Σ_(n=1) ^∞ n(−1)^(n−1) ∫_0 ^(x ) t^(2n−2) e^t dt =Σ_(n=1) ^∞ n(−1)^(n−1) U_n U_n =∫_0 ^x t^(2n−2 ) e^t dt by parts u^′ =t^(2n−2) and v =e^t ⇒ U_n =[(1/(2n−1)) t^(2n−1) e^t ]_0 ^x −∫_0 ^x (1/(2n−1)) t^(2n−1) e^(t ) dt =((x^(2n−1) e^x )/(2n−1)) −(1/(2n−1)) ∫_0 ^x t^(2n−1) e^t dt and ∫_0 ^x t^(2n−1) e^t dt =[(t^(2n) /(2n)) e^t ]_0 ^x −∫_0 ^x (t^(2n) /(2n))e^t dt =((x^(2n) e^x )/(2n)) −(1/(2n)) ∫_0 ^x t^(2n) e^t dt =((x^(2n) e^x )/(2n))−(1/(2n))U_(n+1) ⇒U_n =((x^(2n−1) e^x )/(2n−1))−(1/(2n−1)){((x^(2n) e^x )/(2n))−(1/(2n)) U_(n+1) } =((x^(2n−1) e^x )/(2n−1))−((x^(2n) e^x )/((2n−1)(2n))) +(1/(2n(2n−1))) U_(n+1) ...be continued](Q103032.png)
Answered by maths mind last updated on 12/Jul/20
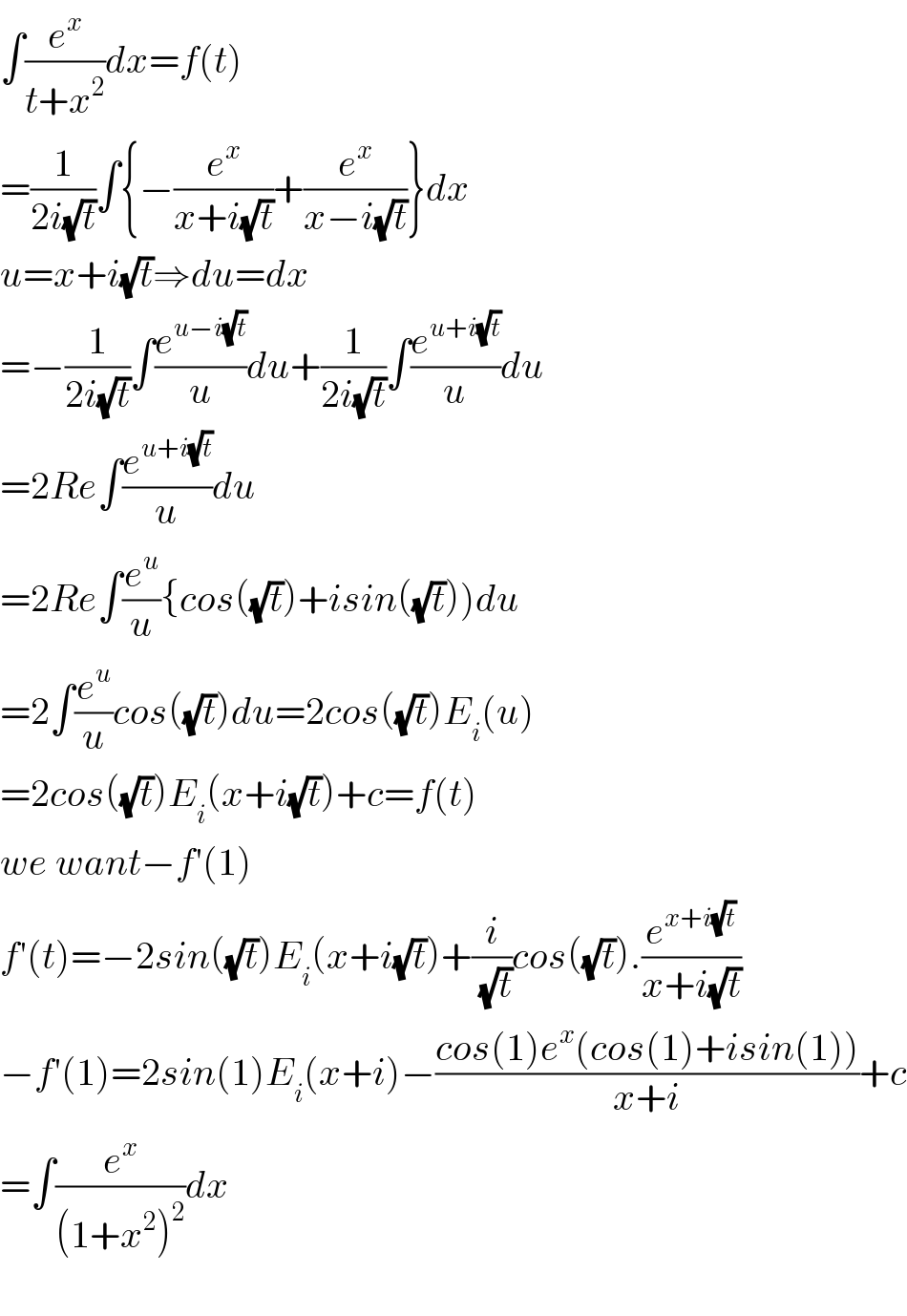
| ||
Question and Answers Forum | ||
Question Number 102985 by DGmichael last updated on 12/Jul/20 | ||
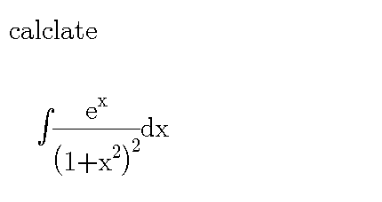 | ||
Answered by mathmax by abdo last updated on 12/Jul/20 | ||
![at form of serie let f(x) =∫_0 ^x (e^t /((1+t^2 )^2 ))dt if o≤x<1 we have (1/(1+u)) =Σ_(n=0) ^∞ (−1)^n u^(n ) ⇒by derivation we get −(1/((1+u)^2 )) =Σ_(n=1) ^∞ n(−1)^n u^(n−1) ⇒(1/((1+u)^2 )) =Σ_(n=1) ^∞ n(−1)^(n−1) u^(n−1) ⇒ (1/((1+t^2 )^2 )) =Σ_(n=1) ^∞ n(−1)^(n−1) t^(2n−2) ⇒f(x) =∫_0 ^(x ) e^t (Σ_(n=1) ^(∞ ) n(−1)^(n−1 ) t^(2n−2) )dt =Σ_(n=1) ^∞ n(−1)^(n−1) ∫_0 ^(x ) t^(2n−2) e^t dt =Σ_(n=1) ^∞ n(−1)^(n−1) U_n U_n =∫_0 ^x t^(2n−2 ) e^t dt by parts u^′ =t^(2n−2) and v =e^t ⇒ U_n =[(1/(2n−1)) t^(2n−1) e^t ]_0 ^x −∫_0 ^x (1/(2n−1)) t^(2n−1) e^(t ) dt =((x^(2n−1) e^x )/(2n−1)) −(1/(2n−1)) ∫_0 ^x t^(2n−1) e^t dt and ∫_0 ^x t^(2n−1) e^t dt =[(t^(2n) /(2n)) e^t ]_0 ^x −∫_0 ^x (t^(2n) /(2n))e^t dt =((x^(2n) e^x )/(2n)) −(1/(2n)) ∫_0 ^x t^(2n) e^t dt =((x^(2n) e^x )/(2n))−(1/(2n))U_(n+1) ⇒U_n =((x^(2n−1) e^x )/(2n−1))−(1/(2n−1)){((x^(2n) e^x )/(2n))−(1/(2n)) U_(n+1) } =((x^(2n−1) e^x )/(2n−1))−((x^(2n) e^x )/((2n−1)(2n))) +(1/(2n(2n−1))) U_(n+1) ...be continued](Q103032.png) | ||
| ||
Answered by maths mind last updated on 12/Jul/20 | ||
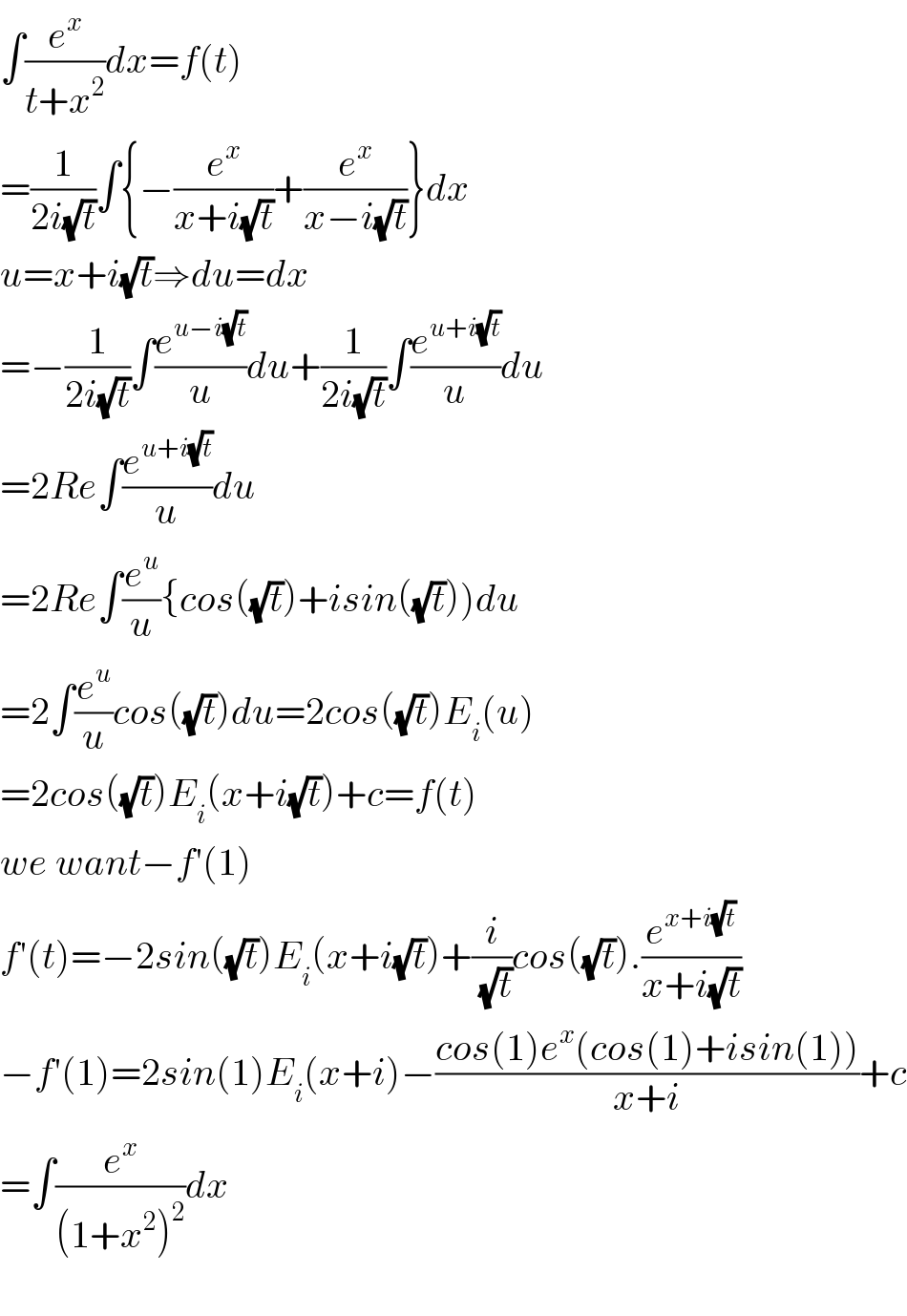 | ||
| ||