Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 103322 by abony1303 last updated on 14/Jul/20

A differentiable function f(x) satisfies f(x^3 −x^2 +x)=2^(x+1) for every real number x. When g(x) is the inverse function of f(x), find g′(4)?

$$\mathrm{A}\:\mathrm{differentiable}\:\mathrm{function}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{satisfies} \\ $$$$\mathrm{f}\left(\mathrm{x}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)=\mathrm{2}^{\mathrm{x}+\mathrm{1}} \:\:\mathrm{for}\:\mathrm{every}\:\mathrm{real}\:\mathrm{number}\:{x}. \\ $$$$\mathrm{When}\:\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{inverse}\:\mathrm{function}\:\mathrm{of}\:\mathrm{f}\left(\mathrm{x}\right), \\ $$$$\mathrm{find}\:\mathrm{g}'\left(\mathrm{4}\right)? \\ $$

Commented by abony1303 last updated on 14/Jul/20

pls help

$$\mathrm{pls}\:\mathrm{help} \\ $$

Answered by Worm_Tail last updated on 14/Jul/20

f(x^3 −x^2 +x)=2^(x+1) ⇒ x^3 −x^2 +x=f^(−1) (2^(x+1) ) x^3 −x^2 +x=g(2^(x+1) ) 3x^2 −2x+1=2^(x+1) ln(2)g′(2^(x+1) )_(x=1) 3−2+1=4ln(2)g′(4) 2=4ln(2)g′(4)⇒g′(4)=(1/(2ln(2)))

$${f}\left({x}^{\mathrm{3}} −{x}^{\mathrm{2}} +{x}\right)=\mathrm{2}^{{x}+\mathrm{1}} \Rightarrow \\ $$$${x}^{\mathrm{3}} −{x}^{\mathrm{2}} +{x}={f}^{−\mathrm{1}} \left(\mathrm{2}^{{x}+\mathrm{1}} \right) \\ $$$${x}^{\mathrm{3}} −{x}^{\mathrm{2}} +{x}={g}\left(\mathrm{2}^{{x}+\mathrm{1}} \right) \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}=\mathrm{2}^{{x}+\mathrm{1}} {ln}\left(\mathrm{2}\right){g}'\left(\mathrm{2}^{{x}+\mathrm{1}} \right)_{{x}=\mathrm{1}} \\ $$$$\mathrm{3}−\mathrm{2}+\mathrm{1}=\mathrm{4}{ln}\left(\mathrm{2}\right){g}'\left(\mathrm{4}\right) \\ $$$$\mathrm{2}=\mathrm{4}{ln}\left(\mathrm{2}\right){g}'\left(\mathrm{4}\right)\Rightarrow{g}'\left(\mathrm{4}\right)=\frac{\mathrm{1}}{\mathrm{2}{ln}\left(\mathrm{2}\right)} \\ $$

Commented by abony1303 last updated on 14/Jul/20

Thank you sir

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by mathmax by abdo last updated on 14/Jul/20

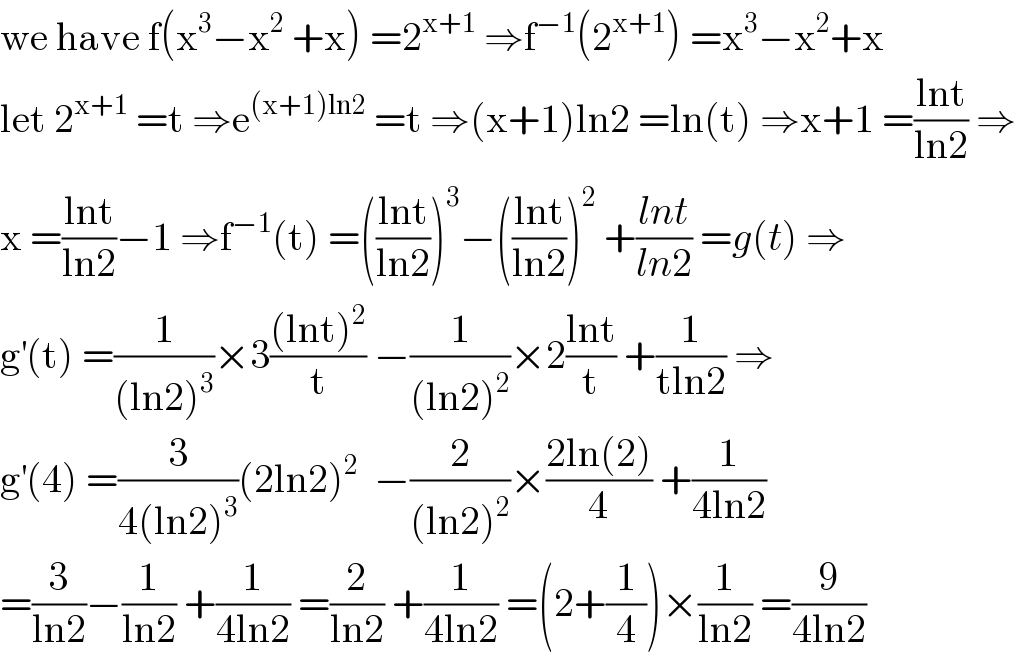
we have f(x^3 −x^2 +x) =2^(x+1) ⇒f^(−1) (2^(x+1) ) =x^3 −x^2 +x let 2^(x+1) =t ⇒e^((x+1)ln2) =t ⇒(x+1)ln2 =ln(t) ⇒x+1 =((lnt)/(ln2)) ⇒ x =((lnt)/(ln2))−1 ⇒f^(−1) (t) =(((lnt)/(ln2)))^3 −(((lnt)/(ln2)))^2 +((lnt)/(ln2)) =g(t) ⇒ g^′ (t) =(1/((ln2)^3 ))×3(((lnt)^2 )/t) −(1/((ln2)^2 ))×2((lnt)/t) +(1/(tln2)) ⇒ g^′ (4) =(3/(4(ln2)^3 ))(2ln2)^2 −(2/((ln2)^2 ))×((2ln(2))/4) +(1/(4ln2)) =(3/(ln2))−(1/(ln2)) +(1/(4ln2)) =(2/(ln2)) +(1/(4ln2)) =(2+(1/4))×(1/(ln2)) =(9/(4ln2))

$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{x}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}\right)\:=\mathrm{2}^{\mathrm{x}+\mathrm{1}} \:\Rightarrow\mathrm{f}^{−\mathrm{1}} \left(\mathrm{2}^{\mathrm{x}+\mathrm{1}} \right)\:=\mathrm{x}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} +\mathrm{x} \\ $$$$\mathrm{let}\:\mathrm{2}^{\mathrm{x}+\mathrm{1}} \:=\mathrm{t}\:\Rightarrow\mathrm{e}^{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{ln2}} \:=\mathrm{t}\:\Rightarrow\left(\mathrm{x}+\mathrm{1}\right)\mathrm{ln2}\:=\mathrm{ln}\left(\mathrm{t}\right)\:\Rightarrow\mathrm{x}+\mathrm{1}\:=\frac{\mathrm{lnt}}{\mathrm{ln2}}\:\Rightarrow \\ $$$$\mathrm{x}\:=\frac{\mathrm{lnt}}{\mathrm{ln2}}−\mathrm{1}\:\Rightarrow\mathrm{f}^{−\mathrm{1}} \left(\mathrm{t}\right)\:=\left(\frac{\mathrm{lnt}}{\mathrm{ln2}}\right)^{\mathrm{3}} −\left(\frac{\mathrm{lnt}}{\mathrm{ln2}}\right)^{\mathrm{2}} \:+\frac{{lnt}}{{ln}\mathrm{2}}\:={g}\left({t}\right)\:\Rightarrow \\ $$$$\mathrm{g}^{'} \left(\mathrm{t}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{ln2}\right)^{\mathrm{3}} }×\mathrm{3}\frac{\left(\mathrm{lnt}\right)^{\mathrm{2}} }{\mathrm{t}}\:−\frac{\mathrm{1}}{\left(\mathrm{ln2}\right)^{\mathrm{2}} }×\mathrm{2}\frac{\mathrm{lnt}}{\mathrm{t}}\:+\frac{\mathrm{1}}{\mathrm{tln2}}\:\Rightarrow \\ $$$$\mathrm{g}^{'} \left(\mathrm{4}\right)\:=\frac{\mathrm{3}}{\mathrm{4}\left(\mathrm{ln2}\right)^{\mathrm{3}} }\left(\mathrm{2ln2}\right)^{\mathrm{2}} \:\:−\frac{\mathrm{2}}{\left(\mathrm{ln2}\right)^{\mathrm{2}} }×\frac{\mathrm{2ln}\left(\mathrm{2}\right)}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{4ln2}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{ln2}}−\frac{\mathrm{1}}{\mathrm{ln2}}\:+\frac{\mathrm{1}}{\mathrm{4ln2}}\:=\frac{\mathrm{2}}{\mathrm{ln2}}\:+\frac{\mathrm{1}}{\mathrm{4ln2}}\:=\left(\mathrm{2}+\frac{\mathrm{1}}{\mathrm{4}}\right)×\frac{\mathrm{1}}{\mathrm{ln2}}\:=\frac{\mathrm{9}}{\mathrm{4ln2}} \\ $$

Commented by 1549442205 last updated on 15/Jul/20

Sir′s the idea is right ,however mistaked at third line:f^(−1) (t)=(((lnt)/(ln2))−1)^3 −(((lnt)/(ln2))−1)^2 +((lnt)/(ln2))−1 =(((lnt)/(ln2)))^3 −3(((lnt)/(ln2)))^2 +3((lnt)/(ln2))−1−[(((lnt)/(ln2)))^2 −2((lnt)/(ln2))+1]+((lnt)/(ln2))−1 =(((lnt)/(ln2)))^3 −4(((lnt)/(ln2)))^2 +6((lnt)/(ln2))−2 g′(t)=(1/((ln2)^3 ))×3(((lnt)^2 )/t)−(4/((ln2)^2 ))×2((lnt)/t)+(6/(tln2)) g′(4)=(3/(ln2))−(4/(ln2))+(3/(2ln2))=(1/(2ln2))

$$\mathrm{Sir}'\mathrm{s}\:\mathrm{the}\:\mathrm{idea}\:\mathrm{is}\:\mathrm{right}\:,\mathrm{however} \\ $$$$\mathrm{mistaked}\:\:\mathrm{at}\:\mathrm{third}\:\mathrm{line}:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{t}\right)=\left(\frac{\mathrm{lnt}}{\mathrm{ln2}}−\mathrm{1}\right)^{\mathrm{3}} −\left(\frac{\mathrm{lnt}}{\mathrm{ln2}}−\mathrm{1}\right)^{\mathrm{2}} +\frac{\mathrm{lnt}}{\mathrm{ln2}}−\mathrm{1} \\ $$$$=\left(\frac{\mathrm{lnt}}{\mathrm{ln2}}\right)^{\mathrm{3}} −\mathrm{3}\left(\frac{\mathrm{lnt}}{\mathrm{ln2}}\right)^{\mathrm{2}} +\mathrm{3}\frac{\mathrm{lnt}}{\mathrm{ln2}}−\mathrm{1}−\left[\left(\frac{\mathrm{lnt}}{\mathrm{ln2}}\right)^{\mathrm{2}} −\mathrm{2}\frac{\mathrm{lnt}}{\mathrm{ln2}}+\mathrm{1}\right]+\frac{\mathrm{lnt}}{\mathrm{ln2}}−\mathrm{1} \\ $$$$=\left(\frac{\mathrm{lnt}}{\mathrm{ln2}}\right)^{\mathrm{3}} −\mathrm{4}\left(\frac{\mathrm{lnt}}{\mathrm{ln2}}\right)^{\mathrm{2}} +\mathrm{6}\frac{\mathrm{lnt}}{\mathrm{ln2}}−\mathrm{2} \\ $$$$\mathrm{g}'\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\left(\mathrm{ln2}\right)^{\mathrm{3}} }×\mathrm{3}\frac{\left(\mathrm{lnt}\right)^{\mathrm{2}} }{\mathrm{t}}−\frac{\mathrm{4}}{\left(\mathrm{ln2}\right)^{\mathrm{2}} }×\mathrm{2}\frac{\mathrm{lnt}}{\mathrm{t}}+\frac{\mathrm{6}}{\mathrm{tln2}} \\ $$$$\mathrm{g}'\left(\mathrm{4}\right)=\frac{\mathrm{3}}{\mathrm{ln2}}−\frac{\mathrm{4}}{\mathrm{ln2}}+\frac{\mathrm{3}}{\mathrm{2ln2}}=\frac{\mathrm{1}}{\mathrm{2ln2}} \\ $$

Commented by mathmax by abdo last updated on 14/Jul/20

yes thank you sir...

$$\mathrm{yes}\:\:\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}... \\ $$

Commented by mathmax by abdo last updated on 14/Jul/20

i forget −1!

$$\mathrm{i}\:\mathrm{forget}\:−\mathrm{1}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com