Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 103591 by mathmax by abdo last updated on 16/Jul/20

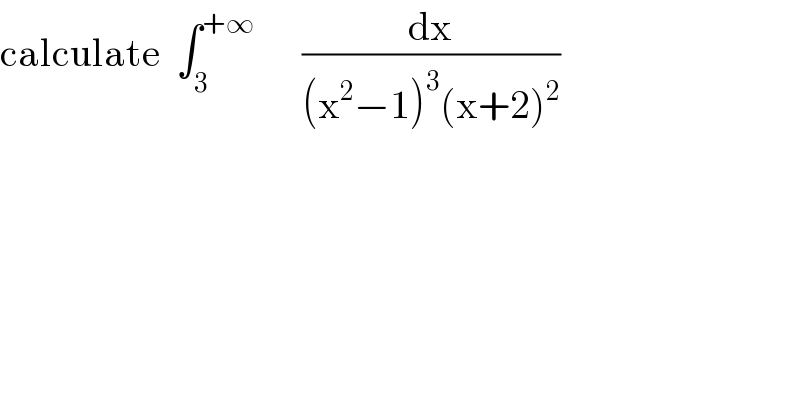
calculate ∫_3 ^(+∞) (dx/((x^2 −1)^3 (x+2)^2 ))

$$\mathrm{calculate}\:\:\int_{\mathrm{3}} ^{+\infty} \:\:\:\:\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$

Commented by Worm_Tail last updated on 16/Jul/20

∫_3 ^(+∞) (dx/((x^2 −1)^3 (x+2)^2 )) pfd ∫_3 ^(oo) ((−3)/(16(x+1)))+(4/(27(x+2)))+(1/(16(x+1)^2 ))+(1/(27(x+2)^2 ))−(1/(8(x+1)^3 ))+((17)/(432(x−1)))−((13)/(432(x−1)^2 ))+(1/(72(x−1)^3 ))dx [((−3ln(x+1))/(16))+(4/(27))ln(x+2)−(1/(16(x+1)))−(1/(27(x+2)))+(1/(16(x+1)^2 ))+((17ln(x−1))/(432))+((13)/(432(x−1)))−(1/(144(x−1)^2 ))]_3 ^(oo) [((ln(((x+2)^(64) (x−1)^(17) )/((x+1)^(81) )))/(432))−(1/(27(x+2)))+(1/(16(x+1)^2 ))+((13)/(432(x−1)))−(1/(144(x−1)^2 ))]_3 ^(oo) lim_(t→oo) [((ln(((t+2)^(64) (t−1)^(17) )/((t+1)^(81) )))/(432))−(1/(27(t+2)))+(1/(16(t+1)^2 ))+((13)/(432(t−1)))−(1/(144(t−1)^2 ))] − [((ln(((3+2)^(64) (3−1)^(17) )/((3+1)^(81) )))/(432))−(1/(27(3+2)))+(1/(16(3+1)^2 ))+((13)/(432(3−1)))−(1/(144(3−1)^2 ))] lim_(t→oo) [((ln(1))/(432))−0+0+0−0]−[((ln((5^(64) ×2^(17) )/4^(81) ))/(432))+((113)/(11520))] −[((64ln(5)−145ln(2))/(432))+((113)/(11520))] ((−64ln(5)+145ln(2))/(432))−((113)/(11520))

$$ \\ $$$$\:\:\:\:\:\int_{\mathrm{3}} ^{+\infty} \:\:\:\:\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} }\:\:\:\:\:{pfd} \\ $$$$\:\:\:\:\:\:\int_{\mathrm{3}} ^{{oo}} \frac{−\mathrm{3}}{\mathrm{16}\left({x}+\mathrm{1}\right)}+\frac{\mathrm{4}}{\mathrm{27}\left({x}+\mathrm{2}\right)}+\frac{\mathrm{1}}{\mathrm{16}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{27}\left({x}+\mathrm{2}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{8}\left({x}+\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{17}}{\mathrm{432}\left({x}−\mathrm{1}\right)}−\frac{\mathrm{13}}{\mathrm{432}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{72}\left({x}−\mathrm{1}\right)^{\mathrm{3}} }{dx} \\ $$$$\:\:\:\:\:\:\left[\frac{−\mathrm{3}{ln}\left({x}+\mathrm{1}\right)}{\mathrm{16}}+\frac{\mathrm{4}}{\mathrm{27}}{ln}\left({x}+\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{16}\left({x}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{27}\left({x}+\mathrm{2}\right)}+\frac{\mathrm{1}}{\mathrm{16}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{17}{ln}\left({x}−\mathrm{1}\right)}{\mathrm{432}}+\frac{\mathrm{13}}{\mathrm{432}\left({x}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{144}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\right]_{\mathrm{3}} ^{{oo}} \\ $$$$\:\:\:\:\:\left[\frac{{ln}\frac{\left({x}+\mathrm{2}\right)^{\mathrm{64}} \left({x}−\mathrm{1}\right)^{\mathrm{17}} }{\left({x}+\mathrm{1}\right)^{\mathrm{81}} }}{\mathrm{432}}−\frac{\mathrm{1}}{\mathrm{27}\left({x}+\mathrm{2}\right)}+\frac{\mathrm{1}}{\mathrm{16}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{13}}{\mathrm{432}\left({x}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{144}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\right]_{\mathrm{3}} ^{{oo}} \\ $$$$\:{li}\underset{{t}\rightarrow{oo}} {{m}}\:\:\:\:\left[\frac{{ln}\frac{\left({t}+\mathrm{2}\right)^{\mathrm{64}} \left({t}−\mathrm{1}\right)^{\mathrm{17}} }{\left({t}+\mathrm{1}\right)^{\mathrm{81}} }}{\mathrm{432}}−\frac{\mathrm{1}}{\mathrm{27}\left({t}+\mathrm{2}\right)}+\frac{\mathrm{1}}{\mathrm{16}\left({t}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{13}}{\mathrm{432}\left({t}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{144}\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\right] \\ $$$$\:−\:\:\:\:\left[\frac{{ln}\frac{\left(\mathrm{3}+\mathrm{2}\right)^{\mathrm{64}} \left(\mathrm{3}−\mathrm{1}\right)^{\mathrm{17}} }{\left(\mathrm{3}+\mathrm{1}\right)^{\mathrm{81}} }}{\mathrm{432}}−\frac{\mathrm{1}}{\mathrm{27}\left(\mathrm{3}+\mathrm{2}\right)}+\frac{\mathrm{1}}{\mathrm{16}\left(\mathrm{3}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{13}}{\mathrm{432}\left(\mathrm{3}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{144}\left(\mathrm{3}−\mathrm{1}\right)^{\mathrm{2}} }\right] \\ $$$$\: \\ $$$$\:{li}\underset{{t}\rightarrow{oo}} {{m}}\:\:\:\:\left[\frac{{ln}\left(\mathrm{1}\right)}{\mathrm{432}}−\mathrm{0}+\mathrm{0}+\mathrm{0}−\mathrm{0}\right]−\left[\frac{{ln}\frac{\mathrm{5}^{\mathrm{64}} ×\mathrm{2}^{\mathrm{17}} }{\mathrm{4}^{\mathrm{81}} }}{\mathrm{432}}+\frac{\mathrm{113}}{\mathrm{11520}}\right] \\ $$$$\:−\left[\frac{\mathrm{64}{ln}\left(\mathrm{5}\right)−\mathrm{145}{ln}\left(\mathrm{2}\right)}{\mathrm{432}}+\frac{\mathrm{113}}{\mathrm{11520}}\right] \\ $$$$\:\frac{−\mathrm{64}{ln}\left(\mathrm{5}\right)+\mathrm{145}{ln}\left(\mathrm{2}\right)}{\mathrm{432}}−\frac{\mathrm{113}}{\mathrm{11520}} \\ $$$$\:\:\:\: \\ $$$$\:\:\:\:\:\: \\ $$

Commented by Worm_Tail last updated on 16/Jul/20

mistake might have crept in

$${mistake}\:\:{might}\:\:\:{have}\:\:\:{crept}\:\:\:{in} \\ $$

Commented by abdomathmax last updated on 16/Jul/20

can you chow how do you find the decomposition?

$$\mathrm{can}\:\mathrm{you}\:\mathrm{chow}\:\mathrm{how}\:\mathrm{do}\:\mathrm{you}\:\mathrm{find}\:\mathrm{the}\:\mathrm{decomposition}? \\ $$

Commented by Worm_Tail last updated on 16/Jul/20

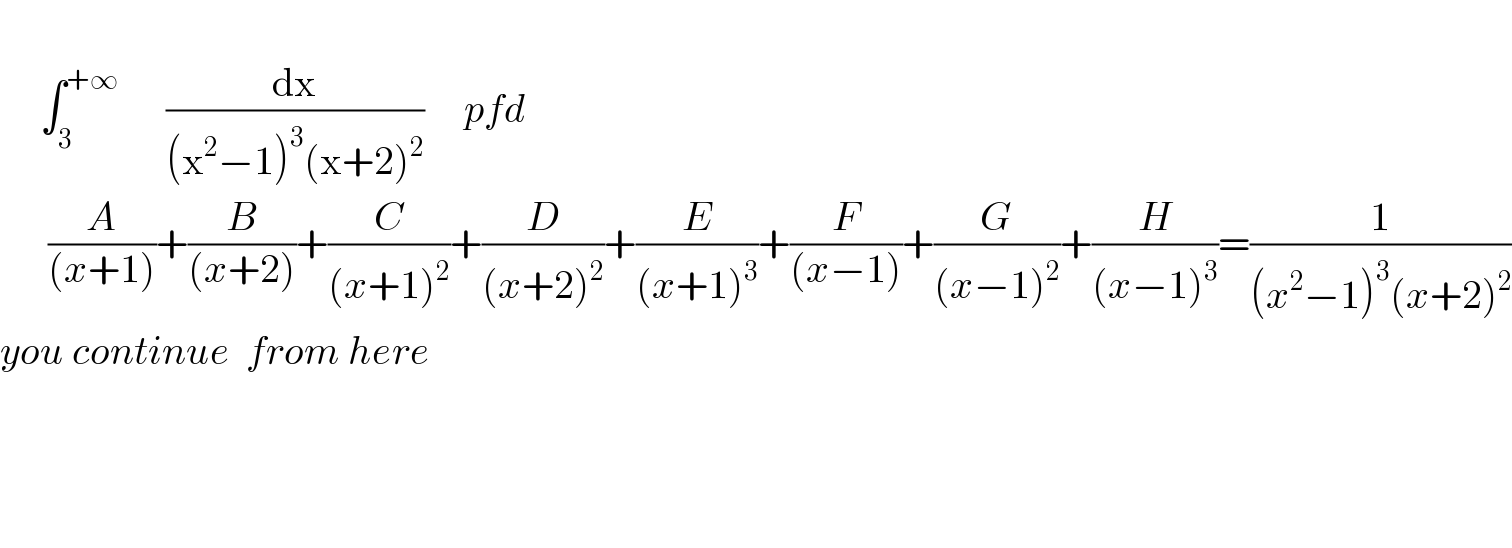
∫_3 ^(+∞) (dx/((x^2 −1)^3 (x+2)^2 )) pfd (A/((x+1)))+(B/((x+2)))+(C/((x+1)^2 ))+(D/((x+2)^2 ))+(E/((x+1)^3 ))+(F/((x−1)))+(G/((x−1)^2 ))+(H/((x−1)^3 ))=(1/((x^2 −1)^3 (x+2)^2 )) you continue from here

$$ \\ $$$$\:\:\:\:\:\int_{\mathrm{3}} ^{+\infty} \:\:\:\:\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} }\:\:\:\:\:{pfd} \\ $$$$\:\:\:\:\:\:\frac{{A}}{\left({x}+\mathrm{1}\right)}+\frac{{B}}{\left({x}+\mathrm{2}\right)}+\frac{{C}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{{D}}{\left({x}+\mathrm{2}\right)^{\mathrm{2}} }+\frac{{E}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }+\frac{{F}}{\left({x}−\mathrm{1}\right)}+\frac{{G}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{{H}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} }=\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} \left({x}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${you}\:{continue}\:\:{from}\:{here} \\ $$$$\: \\ $$$$\:\:\: \\ $$$$\:\:\:\:\:\: \\ $$

Answered by abdomathmax last updated on 16/Jul/20

I =∫_3 ^∞ (dx/((x^2 −1)^3 (x+2)^2 )) ⇒ I =∫_3 ^∞ (dx/((x−1)^3 (x+1)^3 (x+2)^2 )) =∫_3 ^∞ (dx/((((x−1)/(x+1)))^3 (x+1)^6 (x+2)^2 )) we do tbe cha7gement ((x−1)/(x+1)) =t ⇒x−1 =tx+t ⇒(1−t)x =t+1 ⇒ x =((1+t)/(1−t)) ⇒ (dx/dt) =((1−t+(1+t))/((1−t)^2 )) =(2/((1−t)^2 )) x+1 =((1+t)/(1−t)) +1 =((1+t+1−t)/(1−t)) =(2/(1−t)) x+2 =((1+t)/(1−t))+2 =((1+t+2−2t)/(1−t)) =((3−t)/(1−t)) ⇒ I = ∫_(1/2) ^1 ((2dt)/((1−t)^2 t^3 ((2/(1−t)))^6 (((3−t)/(1−t)))^2 )) =2∫_(1/2) ^1 (((t−1)^8 )/((t−1)^2 t^3 .2^6 (3−t)^2 ))dt =(1/2^5 ) ∫_(1/2) ^1 (((t−1)^6 )/(t^3 (3−t)^2 ))dt =(1/2^5 ) ∫_(1/2) ^1 (((t−1)^6 )/(((t/(t−3)))^3 (t−3)^5 ))dt again ch.(t/(t−3)) =z ⇒t =zt−3z ⇒(1−z)t =−3z ⇒ t =((−3z)/(1−z)) =((3z)/(z−1)) and t−3 =((3z)/(z−1))−3 =((3z−3z+3)/(z−1)) =(3/(z−1)) and t−1 =((3z)/(z−1))−1 =((3z−z+1)/(z−1)) =((2z+1)/(z−1)) I =(1/2^5 )∫_(−(1/5)) ^(−(1/2)) (((((2z+1)/(z−1)))^6 )/(z^3 ((3/(z−1)))^5 ))×((−3)/((z−1)^2 ))dz =−(1/(2^5 .3^4 )) ∫_(−(1/5)) ^(−(1/2)) (((2z+1)^6 (z−1)^5 )/(z^3 (z−1)^8 )) dz =−(1/(2^5 .3^4 )) ∫_(−(1/5)) ^(−(1/2)) (((2z+1)^6 )/(z^3 (z−1)^3 ))dz =−(1/(2^5 .3^4 )) ∫_(−(1/5)) ^(−(1/2)) ((Σ_(k=0) ^6 C_6 ^k (2z)^k )/(z^3 (z−1)^3 ))dz =−(1/(2^5 .3^4 )) ∫_(−(1/5)) ^(−(1/2)) Σ_(k=0) ^6 2^k C_6 ^k (z^k /(z^3 (z−1)^3 ))dz =−(1/(2^5 .3^4 )) Σ_(k=0) ^6 2^k C_6 ^k ∫_(−(1/5)) ^(−(1/2)) (z^k /(z^3 (z−1)^3 ))dz after we decompose F_k (z) =(z^k /(z^3 (z−1)^3 )) ...be continued...

$$\mathrm{I}\:=\int_{\mathrm{3}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} }\:\Rightarrow\:\mathrm{I}\:=\int_{\mathrm{3}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{3}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)^{\mathrm{3}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{6}} \left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} }\:\mathrm{we}\:\mathrm{do}\:\mathrm{tbe}\:\mathrm{cha7gement} \\ $$$$\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:=\mathrm{t}\:\Rightarrow\mathrm{x}−\mathrm{1}\:=\mathrm{tx}+\mathrm{t}\:\Rightarrow\left(\mathrm{1}−\mathrm{t}\right)\mathrm{x}\:=\mathrm{t}+\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{x}\:=\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}\:\Rightarrow\:\frac{\mathrm{dx}}{\mathrm{dt}}\:=\frac{\mathrm{1}−\mathrm{t}+\left(\mathrm{1}+\mathrm{t}\right)}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} } \\ $$$$\mathrm{x}+\mathrm{1}\:=\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}\:+\mathrm{1}\:=\frac{\mathrm{1}+\mathrm{t}+\mathrm{1}−\mathrm{t}}{\mathrm{1}−\mathrm{t}}\:=\frac{\mathrm{2}}{\mathrm{1}−\mathrm{t}} \\ $$$$\mathrm{x}+\mathrm{2}\:=\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}+\mathrm{2}\:=\frac{\mathrm{1}+\mathrm{t}+\mathrm{2}−\mathrm{2t}}{\mathrm{1}−\mathrm{t}}\:=\frac{\mathrm{3}−\mathrm{t}}{\mathrm{1}−\mathrm{t}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:\:\frac{\mathrm{2dt}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} \mathrm{t}^{\mathrm{3}} \left(\frac{\mathrm{2}}{\mathrm{1}−\mathrm{t}}\right)^{\mathrm{6}} \left(\frac{\mathrm{3}−\mathrm{t}}{\mathrm{1}−\mathrm{t}}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:\:\:\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{8}} }{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{t}^{\mathrm{3}} \:.\mathrm{2}^{\mathrm{6}} \left(\mathrm{3}−\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:\:\:\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{6}} }{\mathrm{t}^{\mathrm{3}} \left(\mathrm{3}−\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{6}} }{\left(\frac{\mathrm{t}}{\mathrm{t}−\mathrm{3}}\right)^{\mathrm{3}} \left(\mathrm{t}−\mathrm{3}\right)^{\mathrm{5}} }\mathrm{dt} \\ $$$$\mathrm{again}\:\mathrm{ch}.\frac{\mathrm{t}}{\mathrm{t}−\mathrm{3}}\:=\mathrm{z}\:\Rightarrow\mathrm{t}\:\:=\mathrm{zt}−\mathrm{3z}\:\Rightarrow\left(\mathrm{1}−\mathrm{z}\right)\mathrm{t}\:=−\mathrm{3z}\:\Rightarrow \\ $$$$\mathrm{t}\:=\frac{−\mathrm{3z}}{\mathrm{1}−\mathrm{z}}\:=\frac{\mathrm{3z}}{\mathrm{z}−\mathrm{1}}\:\mathrm{and}\:\mathrm{t}−\mathrm{3}\:=\frac{\mathrm{3z}}{\mathrm{z}−\mathrm{1}}−\mathrm{3}\:=\frac{\mathrm{3z}−\mathrm{3z}+\mathrm{3}}{\mathrm{z}−\mathrm{1}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{z}−\mathrm{1}}\:\:\mathrm{and}\:\mathrm{t}−\mathrm{1}\:=\frac{\mathrm{3z}}{\mathrm{z}−\mathrm{1}}−\mathrm{1}\:=\frac{\mathrm{3z}−\mathrm{z}+\mathrm{1}}{\mathrm{z}−\mathrm{1}}\:=\frac{\mathrm{2z}+\mathrm{1}}{\mathrm{z}−\mathrm{1}} \\ $$$$\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }\int_{−\frac{\mathrm{1}}{\mathrm{5}}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\:\frac{\left(\frac{\mathrm{2z}+\mathrm{1}}{\mathrm{z}−\mathrm{1}}\right)^{\mathrm{6}} }{\mathrm{z}^{\mathrm{3}} \left(\frac{\mathrm{3}}{\mathrm{z}−\mathrm{1}}\right)^{\mathrm{5}} }×\frac{−\mathrm{3}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dz} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} .\mathrm{3}^{\mathrm{4}} }\:\int_{−\frac{\mathrm{1}}{\mathrm{5}}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\:\:\frac{\left(\mathrm{2z}+\mathrm{1}\right)^{\mathrm{6}} \left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{5}} }{\mathrm{z}^{\mathrm{3}} \left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{8}} }\:\mathrm{dz} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} .\mathrm{3}^{\mathrm{4}} }\:\int_{−\frac{\mathrm{1}}{\mathrm{5}}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\:\frac{\left(\mathrm{2z}+\mathrm{1}\right)^{\mathrm{6}} }{\mathrm{z}^{\mathrm{3}} \left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dz} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} .\mathrm{3}^{\mathrm{4}} }\:\int_{−\frac{\mathrm{1}}{\mathrm{5}}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{6}} \:\mathrm{C}_{\mathrm{6}} ^{\mathrm{k}} \left(\mathrm{2z}\right)^{\mathrm{k}} }{\mathrm{z}^{\mathrm{3}} \left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dz} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} .\mathrm{3}^{\mathrm{4}} }\:\int_{−\frac{\mathrm{1}}{\mathrm{5}}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} \sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{6}} \:\mathrm{2}^{\mathrm{k}} \:\mathrm{C}_{\mathrm{6}} ^{\mathrm{k}} \:\frac{\mathrm{z}^{\mathrm{k}} }{\mathrm{z}^{\mathrm{3}} \left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dz} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} .\mathrm{3}^{\mathrm{4}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{6}} \:\mathrm{2}^{\mathrm{k}} \:\mathrm{C}_{\mathrm{6}} ^{\mathrm{k}} \:\int_{−\frac{\mathrm{1}}{\mathrm{5}}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\mathrm{z}^{\mathrm{k}} }{\mathrm{z}^{\mathrm{3}} \left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dz} \\ $$$$\mathrm{after}\:\mathrm{we}\:\mathrm{decompose}\:\mathrm{F}_{\mathrm{k}} \left(\mathrm{z}\right)\:=\frac{\mathrm{z}^{\mathrm{k}} }{\mathrm{z}^{\mathrm{3}} \left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$...\mathrm{be}\:\mathrm{continued}... \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com