Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 10374 by ridwan balatif last updated on 06/Feb/17

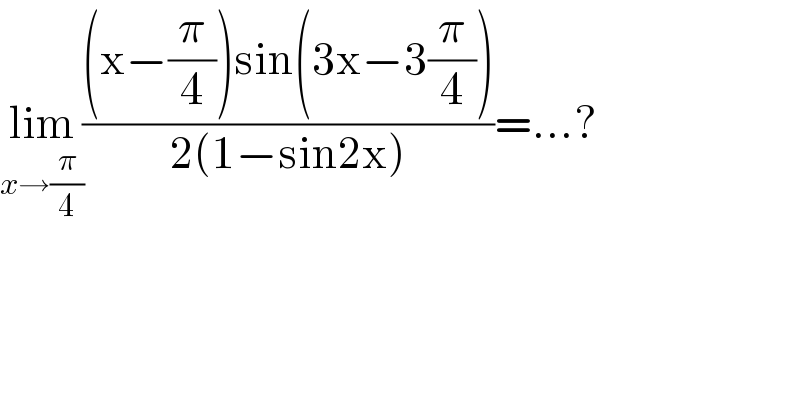
lim_(x→(π/4)) (((x−(π/4))sin(3x−3(π/4)))/(2(1−sin2x)))=...?

$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\frac{\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)\mathrm{sin}\left(\mathrm{3x}−\mathrm{3}\frac{\pi}{\mathrm{4}}\right)}{\mathrm{2}\left(\mathrm{1}−\mathrm{sin2x}\right)}=...? \\ $$

Answered by mrW1 last updated on 06/Feb/17

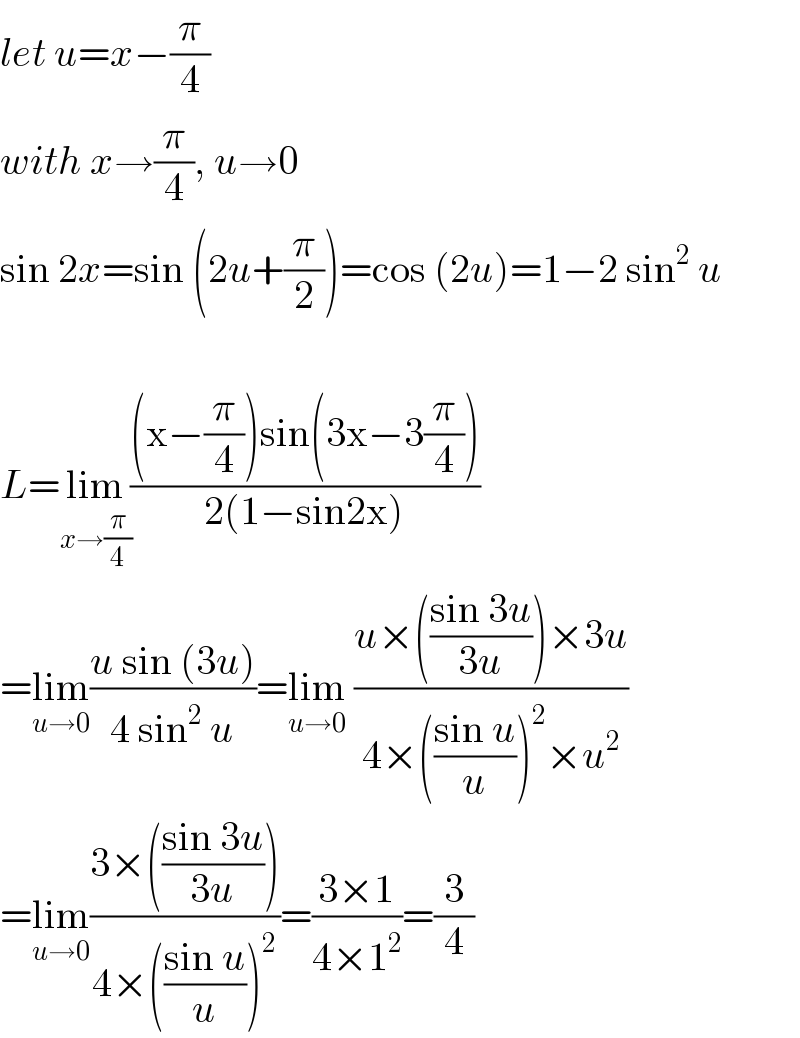
let u=x−(π/4) with x→(π/4), u→0 sin 2x=sin (2u+(π/2))=cos (2u)=1−2 sin^2 u L=lim_(x→(π/4)) (((x−(π/4))sin(3x−3(π/4)))/(2(1−sin2x))) =lim_(u→0) ((u sin (3u))/(4 sin^2 u))=lim_(u→0) ((u×(((sin 3u)/(3u)))×3u)/(4×(((sin u)/u))^2 ×u^2 )) =lim_(u→0) ((3×(((sin 3u)/(3u))))/(4×(((sin u)/u))^2 ))=((3×1)/(4×1^2 ))=(3/4)

$${let}\:{u}={x}−\frac{\pi}{\mathrm{4}} \\ $$$${with}\:{x}\rightarrow\frac{\pi}{\mathrm{4}},\:{u}\rightarrow\mathrm{0} \\ $$$$\mathrm{sin}\:\mathrm{2}{x}=\mathrm{sin}\:\left(\mathrm{2}{u}+\frac{\pi}{\mathrm{2}}\right)=\mathrm{cos}\:\left(\mathrm{2}{u}\right)=\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:{u} \\ $$$$ \\ $$$${L}=\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\frac{\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)\mathrm{sin}\left(\mathrm{3x}−\mathrm{3}\frac{\pi}{\mathrm{4}}\right)}{\mathrm{2}\left(\mathrm{1}−\mathrm{sin2x}\right)} \\ $$$$=\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{u}\:\mathrm{sin}\:\left(\mathrm{3}{u}\right)}{\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:{u}}=\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{u}×\left(\frac{\mathrm{sin}\:\mathrm{3}{u}}{\mathrm{3}{u}}\right)×\mathrm{3}{u}}{\mathrm{4}×\left(\frac{\mathrm{sin}\:{u}}{{u}}\right)^{\mathrm{2}} ×{u}^{\mathrm{2}} } \\ $$$$=\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}×\left(\frac{\mathrm{sin}\:\mathrm{3}{u}}{\mathrm{3}{u}}\right)}{\mathrm{4}×\left(\frac{\mathrm{sin}\:{u}}{{u}}\right)^{\mathrm{2}} }=\frac{\mathrm{3}×\mathrm{1}}{\mathrm{4}×\mathrm{1}^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{4}} \\ $$

Commented by ridwan balatif last updated on 06/Feb/17

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by arge last updated on 08/Feb/17

por l′hopital, y=(((x−(x/4))sen(3x−((12+π)/4)))/(2(1−sen2x))) y′=((2(1−sen2x)[(x−(x/4))cos(3x−((12+π)/4))+sen(3x−((12+π)/4))(1−(1/4))]−(x−(x/4))sen(3x−((12+π)/4))×2(−cos2x))/(4(1−2sen2x+4sen^2 xcos^2 x))) y′=(A/0) A=_ −134.65, y′=∞∵∵∵∵∵Rta

$${por}\:{l}'{hopital}, \\ $$$$ \\ $$$${y}=\frac{\left({x}−\frac{{x}}{\mathrm{4}}\right){sen}\left(\mathrm{3}{x}−\frac{\mathrm{12}+\pi}{\mathrm{4}}\right)}{\mathrm{2}\left(\mathrm{1}−{sen}\mathrm{2}{x}\right)} \\ $$$$ \\ $$$${y}'=\frac{\mathrm{2}\left(\mathrm{1}−{sen}\mathrm{2}{x}\right)\left[\left({x}−\frac{{x}}{\mathrm{4}}\right){cos}\left(\mathrm{3}{x}−\frac{\mathrm{12}+\pi}{\mathrm{4}}\right)+{sen}\left(\mathrm{3}{x}−\frac{\mathrm{12}+\pi}{\mathrm{4}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right)\right]−\left({x}−\frac{{x}}{\mathrm{4}}\right){sen}\left(\mathrm{3}{x}−\frac{\mathrm{12}+\pi}{\mathrm{4}}\right)×\mathrm{2}\left(−{cos}\mathrm{2}{x}\right)}{\mathrm{4}\left(\mathrm{1}−\mathrm{2}{sen}\mathrm{2}{x}+\mathrm{4}{sen}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}\right)} \\ $$$$ \\ $$$${y}'=\frac{{A}}{\mathrm{0}} \\ $$$$ \\ $$$${A}\underset{} {=}\:\:−\mathrm{134}.\mathrm{65},\:{y}'=\infty\because\because\because\because\because{Rta} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Answered by bahmanfeshki last updated on 02/Mar/17

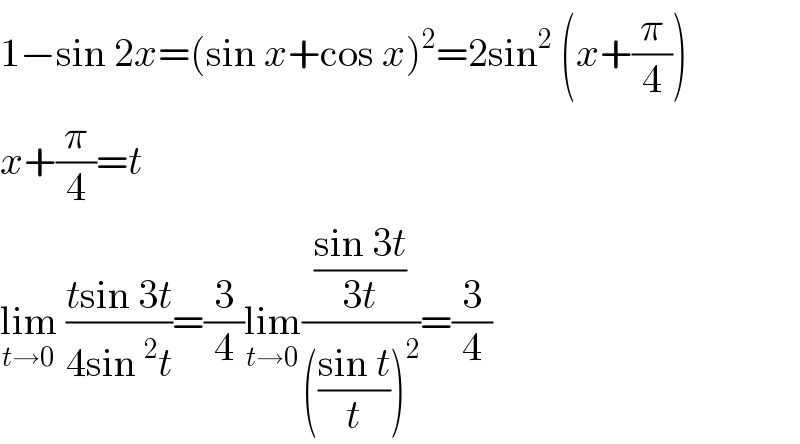
1−sin 2x=(sin x+cos x)^2 =2sin^2 (x+(π/4)) x+(π/4)=t lim_(t→0) ((tsin 3t)/(4sin^2 t))=(3/4)lim_(t→0) (((sin 3t)/(3t))/((((sin t)/t))^2 ))=(3/4)

$$\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}=\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} =\mathrm{2sin}^{\mathrm{2}} \:\left({x}+\frac{\pi}{\mathrm{4}}\right) \\ $$$${x}+\frac{\pi}{\mathrm{4}}={t} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{t}\mathrm{sin}\:\mathrm{3}{t}}{\mathrm{4sin}\:^{\mathrm{2}} {t}}=\frac{\mathrm{3}}{\mathrm{4}}\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{sin}\:\mathrm{3}{t}}{\mathrm{3}{t}}}{\left(\frac{\mathrm{sin}\:{t}}{{t}}\right)^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{4}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com