Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 104104 by bemath last updated on 19/Jul/20

∫ ((xtan^(−1) (x))/(√(1+x^2 ))) dx ?

$$\int\:\frac{{x}\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx}\:? \\ $$

Answered by OlafThorendsen last updated on 19/Jul/20

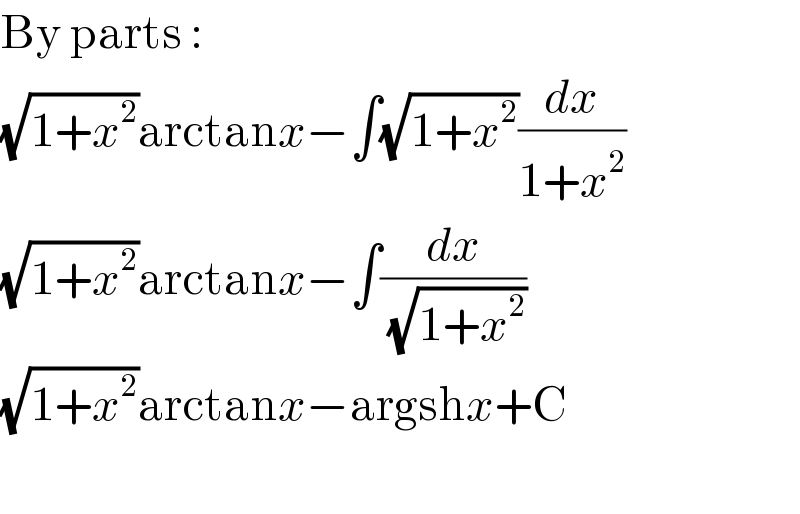
By parts : (√(1+x^2 ))arctanx−∫(√(1+x^2 ))(dx/(1+x^2 )) (√(1+x^2 ))arctanx−∫(dx/(√(1+x^2 ))) (√(1+x^2 ))arctanx−argshx+C

$$\mathrm{By}\:\mathrm{parts}\:: \\ $$$$\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\mathrm{arctan}{x}−\int\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\mathrm{arctan}{x}−\int\frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$$\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\mathrm{arctan}{x}−\mathrm{argsh}{x}+\mathrm{C} \\ $$$$ \\ $$

Answered by Dwaipayan Shikari last updated on 19/Jul/20

∫((θtanθ)/(secθ)) sec^2 θdθ {x=tanθ ⇒1=sec^2 θ(dθ/dx) ∫θsecθtanθ θ∫secθtanθ−∫∫secθtanθ θsecθ−log(secθ+tanθ)+C tan^(−1) x sec(tan^(−1) x)−log(sec(tan^(−1) x)+x)+C Another way tan^(−1) x.(1/2)∫((2x)/(√(x^2 +1)))−∫(1/(x^2 +1)).(1/2)∫((2x)/(√(x^2 +1))) tan^(−1) x(√(x^2 +1))−∫(dx/(√(x^2 +1)))=tan^(−1) x (√(x^2 +1))−log(x+(√(x^2 +1)))+C

$$\int\frac{\theta{tan}\theta}{{sec}\theta}\:{sec}^{\mathrm{2}} \theta{d}\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{{x}={tan}\theta\:\:\Rightarrow\mathrm{1}={sec}^{\mathrm{2}} \theta\frac{{d}\theta}{{dx}}\right. \\ $$$$\int\theta{sec}\theta{tan}\theta \\ $$$$\theta\int{sec}\theta{tan}\theta−\int\int{sec}\theta{tan}\theta \\ $$$$\theta{sec}\theta−{log}\left({sec}\theta+{tan}\theta\right)+{C} \\ $$$${tan}^{−\mathrm{1}} {x}\:{sec}\left({tan}^{−\mathrm{1}} {x}\right)−{log}\left({sec}\left({tan}^{−\mathrm{1}} {x}\right)+{x}\right)+{C} \\ $$$$ \\ $$$$ \\ $$$${Another}\:{way} \\ $$$$ \\ $$$$ \\ $$$${tan}^{−\mathrm{1}} {x}.\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}}{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}−\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}.\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}}{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${tan}^{−\mathrm{1}} {x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−\int\frac{{dx}}{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}={tan}^{−\mathrm{1}} {x}\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{log}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)+{C} \\ $$

Answered by bobhans last updated on 19/Jul/20

∫ tan^(−1) (x) d((√(1+x^2 ))) = (√(1+x^2 )) tan^(−1) (x)−∫ ((√(1+x^2 ))/(1+x^2 )) dx = (√(1+x^2 )) tan^(−1) (x)−∫ (dx/(√(1+x^2 ))) let I_1 = ∫ (dx/(√(1+x^2 ))) [ x = tan p ] I_1 = ∫ ((sec^2 p)/(sec p)) dp = ∫ sec p dp I_1 = ln ∣sec p + tan p ∣ + c ∴ I = (√(1+x^2 )) tan^(−1) (x)−ln ∣(√(1+x^2 )) +x∣ + c

$$\int\:\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\:{d}\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:=\: \\ $$$$\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\mathrm{tan}^{−\mathrm{1}} \left({x}\right)−\int\:\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:= \\ $$$$\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\mathrm{tan}^{−\mathrm{1}} \left({x}\right)−\int\:\frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$${let}\:{I}_{\mathrm{1}} =\:\int\:\frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:\:\left[\:{x}\:=\:\mathrm{tan}\:{p}\:\right] \\ $$$${I}_{\mathrm{1}} =\:\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} {p}}{\mathrm{sec}\:{p}}\:{dp}\:=\:\int\:\mathrm{sec}\:{p}\:{dp} \\ $$$${I}_{\mathrm{1}} =\:\mathrm{ln}\:\mid\mathrm{sec}\:{p}\:+\:\mathrm{tan}\:{p}\:\mid\:+\:{c}\: \\ $$$$\therefore\:{I}\:=\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\mathrm{tan}^{−\mathrm{1}} \left({x}\right)−\mathrm{ln}\:\mid\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+{x}\mid\:+\:{c} \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 19/Jul/20

I =∫ ((xarctanx)/(√(1+x^2 )))dx by parts u^′ =(x/(√(1+x^2 ))) and v =arctanx ⇒ I =(√(1+x^2 )) arctanx −∫ (√(1+x^2 ))×(dx/(1+x^2 )) =arctanx(√(1+x^2 )) −∫ (dx/(√(1+x^2 ))) =arctan(x)(√(1+x^2 )) −ln(x+(√(1+x^2 ))) +C

$$\mathrm{I}\:=\int\:\:\frac{\mathrm{xarctanx}}{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}\:\:\:\mathrm{by}\:\mathrm{parts}\:\mathrm{u}^{'} \:=\frac{\mathrm{x}}{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\:\mathrm{and}\:\mathrm{v}\:=\mathrm{arctanx}\:\Rightarrow \\ $$$$\mathrm{I}\:=\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{arctanx}\:−\int\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }×\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\mathrm{arctanx}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:−\int\:\frac{\mathrm{dx}}{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }} \\ $$$$=\mathrm{arctan}\left(\mathrm{x}\right)\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:−\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\:+\mathrm{C} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com