
Question and Answers Forum
Question Number 104197 by mathmax by abdo last updated on 20/Jul/20
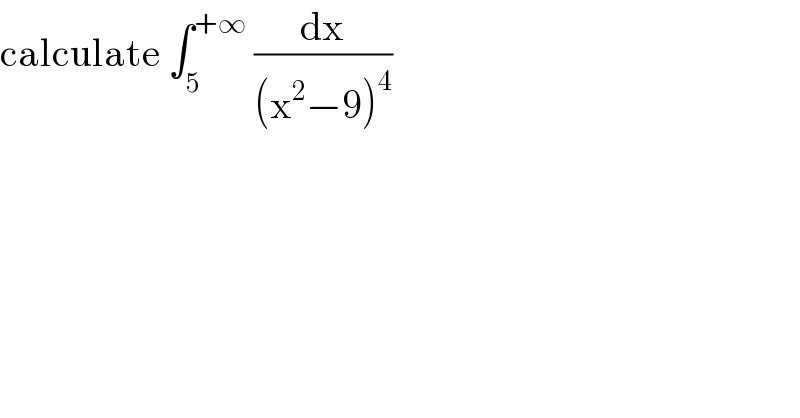
Answered by Dwaipayan Shikari last updated on 20/Jul/20

Answered by mathmax by abdo last updated on 20/Jul/20
![A =∫_5 ^∞ (dx/((x^2 −9)^4 )) ⇒A =∫_5 ^∞ (dx/((x−3)^4 (x+3)^4 )) =∫_5 ^∞ (dx/((((x−3)/(x+3)))^4 (x+3)^8 )) we do the changement ((x−3)/(x+3)) =t ⇒x−3 =tx+3t ⇒(1−t)x =3t+3 ⇒x =((3t+3)/(1−t)) (dx/dx) =((3(1−t)+(3t+3))/((1−t)^2 )) =(6/((1−t)^2 )) x+3 =((3t+3)/(1−t)) +3 =((3t+3+3−3t)/(1−t)) =(6/(1−t)) ⇒A =∫_(1/4) ^1 (6/((1−t)^2 t^4 ((6/(1−t)))^8 ))dt =(1/6^7 ) ∫_(1/4) ^1 (((t−1)^8 )/((t−1)^2 t^4 ))dt =(1/6^7 ) ∫_(1/4) ^1 (((t−1)^6 )/t^4 ) dt =(1/6^7 ) ∫_(1/4) ^1 ((Σ_(k=0) ^6 C_6 ^(k ) t^k )/t^4 )dt =(1/6^7 ) Σ_(k=0) ^6 C_6 ^k ∫_(1/4) ^1 t^(k−4) dt =(1/6^7 ) Σ_(k=0and k≠3) ^6 C_6 ^k [(1/(k−3))t^(k−3) ]_(1/4) ^1 +(1/6^7 )C_6 ^3 [lnt]_(1/4) ^1 A =(1/6^7 ) Σ_(k=0 and k≠3) ^6 (C_6 ^k /(k−3)){1−(1/4^(k−3) )} +(C_6 ^3 /6^7 )×(2ln2)](Q104261.png)
| ||
Question and Answers Forum | ||
Question Number 104197 by mathmax by abdo last updated on 20/Jul/20 | ||
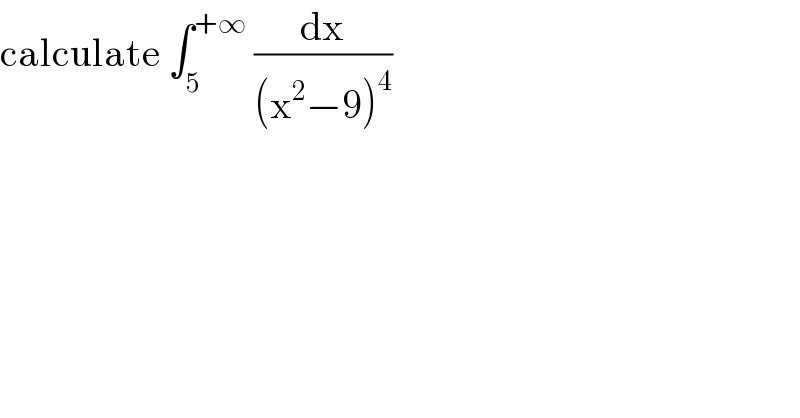 | ||
Answered by Dwaipayan Shikari last updated on 20/Jul/20 | ||
 | ||
| ||
Answered by mathmax by abdo last updated on 20/Jul/20 | ||
![A =∫_5 ^∞ (dx/((x^2 −9)^4 )) ⇒A =∫_5 ^∞ (dx/((x−3)^4 (x+3)^4 )) =∫_5 ^∞ (dx/((((x−3)/(x+3)))^4 (x+3)^8 )) we do the changement ((x−3)/(x+3)) =t ⇒x−3 =tx+3t ⇒(1−t)x =3t+3 ⇒x =((3t+3)/(1−t)) (dx/dx) =((3(1−t)+(3t+3))/((1−t)^2 )) =(6/((1−t)^2 )) x+3 =((3t+3)/(1−t)) +3 =((3t+3+3−3t)/(1−t)) =(6/(1−t)) ⇒A =∫_(1/4) ^1 (6/((1−t)^2 t^4 ((6/(1−t)))^8 ))dt =(1/6^7 ) ∫_(1/4) ^1 (((t−1)^8 )/((t−1)^2 t^4 ))dt =(1/6^7 ) ∫_(1/4) ^1 (((t−1)^6 )/t^4 ) dt =(1/6^7 ) ∫_(1/4) ^1 ((Σ_(k=0) ^6 C_6 ^(k ) t^k )/t^4 )dt =(1/6^7 ) Σ_(k=0) ^6 C_6 ^k ∫_(1/4) ^1 t^(k−4) dt =(1/6^7 ) Σ_(k=0and k≠3) ^6 C_6 ^k [(1/(k−3))t^(k−3) ]_(1/4) ^1 +(1/6^7 )C_6 ^3 [lnt]_(1/4) ^1 A =(1/6^7 ) Σ_(k=0 and k≠3) ^6 (C_6 ^k /(k−3)){1−(1/4^(k−3) )} +(C_6 ^3 /6^7 )×(2ln2)](Q104261.png) | ||
| ||