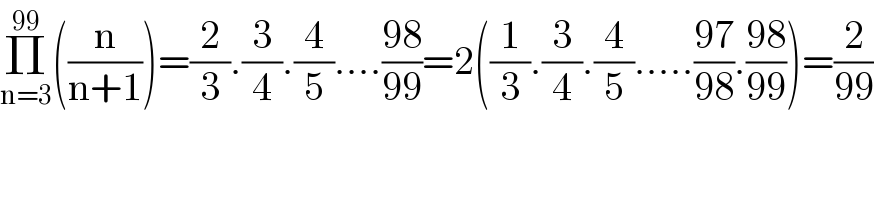Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 104246 by Anindita last updated on 20/Jul/20

$$(1-\frac{1}{3})(1-\frac{1}{4})(1-\frac{1}{5})....(1-\frac{1}{99})=?$$

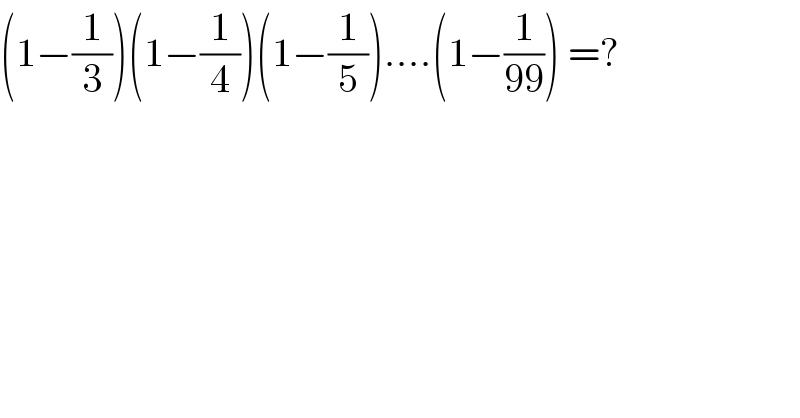
Answered by mathmax by abdo last updated on 20/Jul/20

$$\mathrm{let}{\mathrm{A}}_{\mathrm{n}}=(1-\frac{1}{3})(1-\frac{1}{4})....(1-\frac{1}{\mathrm{n}})\Rightarrow {\mathrm{A}}_{\mathrm{n}}=\frac{2}{3}\times \frac{3}{4}\times \frac{4}{5}\times ...\frac{\mathrm{n}-2}{\mathrm{n}-1}\times \frac{\mathrm{n}-1}{\mathrm{n}}$$$$\Rightarrow {\mathrm{A}}_{\mathrm{n}}=\frac{2}{\mathrm{n}}\mathrm{and}(1-\frac{1}{3})(1-\frac{1}{4})...(1-\frac{1}{99})=\frac{2}{99}$$

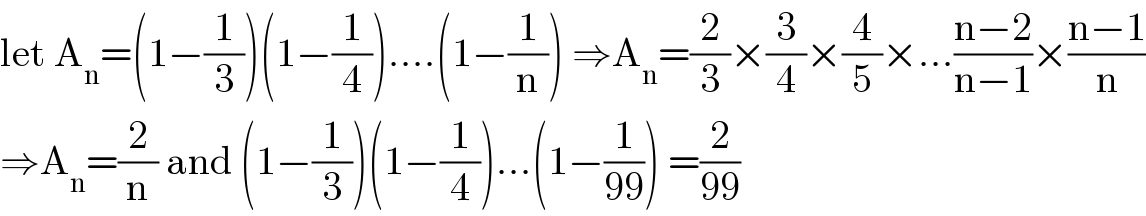
Answered by OlafThorendsen last updated on 20/Jul/20

$$\mathrm{P}=\underset{k=3}{\prod ^{99}}(1-\frac{1}{k})$$$$\mathrm{P}=\underset{k=3}{\prod ^{99}}\frac{k-1}{k}$$$$\mathrm{P}=\frac{2}{3}\times \frac{3}{4}\times \frac{4}{5}....\frac{97}{98}\times \frac{98}{99}$$$$\mathrm{P}=\frac{2}{99}$$

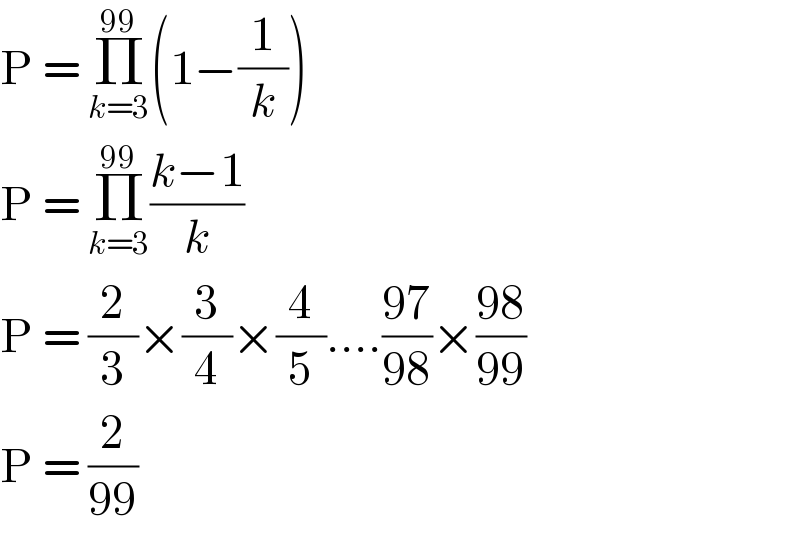
Answered by Dwaipayan Shikari last updated on 20/Jul/20

$$\underset{\mathrm{n}=3}{\prod ^{99}}\left(\frac{\mathrm{n}}{\mathrm{n}+1}\right)=\frac{2}{3}.\frac{3}{4}.\frac{4}{5}....\frac{98}{99}=2(\frac{1}{3}.\frac{3}{4}.\frac{4}{5}.....\frac{97}{98}.\frac{98}{99})=\frac{2}{99}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com