Question Number 104609 by M±th+et+s last updated on 22/Jul/20
$${prove}: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{4}} \left(\mathrm{1}−{x}\right)^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{22}}{\mathrm{7}}−\pi \\ $$
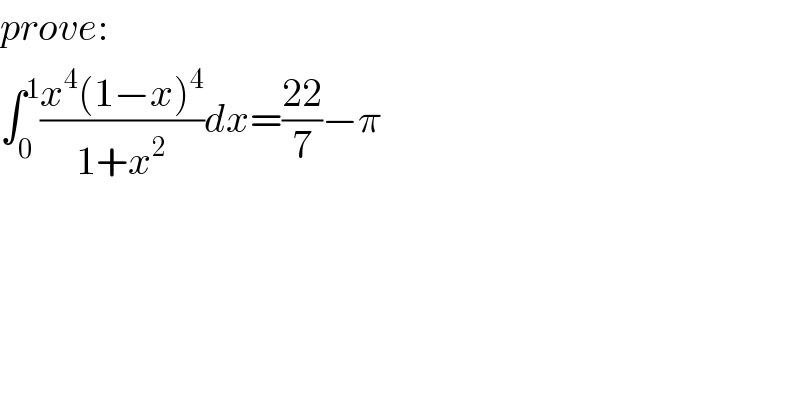
Answered by Dwaipayan Shikari last updated on 22/Jul/20
![∫_0 ^1 ((x^4 (1−2x+x^2 )^2 )/(1+x^2 ))dx ∫_0 ^1 ((x^4 ((1+x^2 )^2 −4x(1+x^2 )+4x^2 ))/(1+x^2 ))dx ∫_0 ^1 x^4 (1+x^2 )−4x^5 +((4x^6 )/(1+x^2 ))dx ∫_0 ^1 x^4 +x^6 −4x^5 +((4x^6 +4)/(1+x^2 ))−(4/(1+x^2 ))dx [(x^5 /5)+(x^7 /7)−((4x^6 )/6)]_0 ^1 +∫4(x^4 −x^2 +1)−[4 tan^(−1) x]_0 ^1 (1/5)+(1/7)−(2/3)+(4/5)−(4/3)+4−4.(π/4) =1+(1/7)−2+4−π =3+(1/7)−π =((22)/7)−π It proves that 𝛑 is smaller than ((22)/7)](Q104612.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{4}} \left(\mathrm{1}−\mathrm{2}{x}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{4}} \left(\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+\mathrm{4}{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{4}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\mathrm{4}{x}^{\mathrm{5}} +\frac{\mathrm{4}{x}^{\mathrm{6}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{4}} +{x}^{\mathrm{6}} −\mathrm{4}{x}^{\mathrm{5}} +\frac{\mathrm{4}{x}^{\mathrm{6}} +\mathrm{4}}{\mathrm{1}+{x}^{\mathrm{2}} }−\frac{\mathrm{4}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\left[\frac{{x}^{\mathrm{5}} }{\mathrm{5}}+\frac{{x}^{\mathrm{7}} }{\mathrm{7}}−\frac{\mathrm{4}{x}^{\mathrm{6}} }{\mathrm{6}}\right]_{\mathrm{0}} ^{\mathrm{1}} +\int\mathrm{4}\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)−\left[\mathrm{4}\:{tan}^{−\mathrm{1}} {x}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{7}}−\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{4}}{\mathrm{5}}−\frac{\mathrm{4}}{\mathrm{3}}+\mathrm{4}−\mathrm{4}.\frac{\pi}{\mathrm{4}} \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{7}}−\mathrm{2}+\mathrm{4}−\pi \\ $$$$=\mathrm{3}+\frac{\mathrm{1}}{\mathrm{7}}−\pi \\ $$$$=\frac{\mathrm{22}}{\mathrm{7}}−\pi\:\:\: \\ $$$$\mathrm{It}\:\mathrm{proves}\:\boldsymbol{\mathrm{that}}\:\boldsymbol{\pi}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{smaller}}\:\boldsymbol{\mathrm{than}}\:\frac{\mathrm{22}}{\mathrm{7}} \\ $$
Commented by Dwaipayan Shikari last updated on 22/Jul/20
����
Commented by Ar Brandon last updated on 22/Jul/20
Great decomposition ��
Commented by M±th+et+s last updated on 22/Jul/20
$${nice}\:{work}\:{sir} \\ $$
Commented by Dwaipayan Shikari last updated on 22/Jul/20
������