
Question and Answers Forum
Question Number 104774 by mathmax by abdo last updated on 23/Jul/20
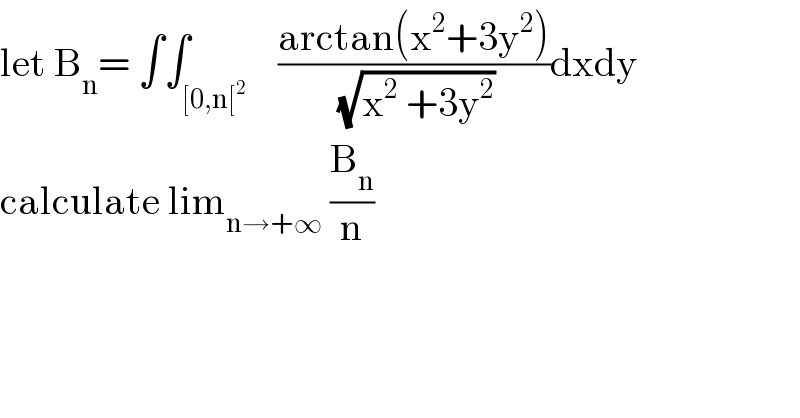
Answered by mathmax by abdo last updated on 26/Jul/20

Commented by mathmax by abdo last updated on 26/Jul/20
![=(1/(2(√2))){ ln((√((r+(1/r)−(√2))/(r+(1/r)+(√2))))) +arctan((1/(√2))(r−(1/r))) +c ⇒ ∫_0 ^(2n) arctan(r^2 )dr =[r arctan(r^2 )]_0 ^(2n) −(1/(√2))[{ln((√((r^2 +1−(√2)r)/(r^2 +1+(√2)r)))) +arctan((1/(√2))(r−(1/r)))]_0 ^(2n) =2n arctan(4n^2 )−(1/(√2)){ln((√((4n^2 +1−2(√2)n)/(4n^2 +1+2(√2)n))))+arctan((1/(√2))(2n−(1/(2n)))=u_n +(π/2)} ⇒B_n =(π/2)u_n ⇒(B_n /n) =(π/2)(u_n /n) =π arctan(4n^2 ) −(1/(n(√2))){ln(√((4n^2 +1−2(√2)n)/(4n^2 +1+2(√2)n)))+arctan((1/(√2))(2n−(1/n))} ⇒lim_(n→+∞) (B_n /n) =π×(π/2) =(π^2 /2)](Q105172.png)
| ||
Question and Answers Forum | ||
Question Number 104774 by mathmax by abdo last updated on 23/Jul/20 | ||
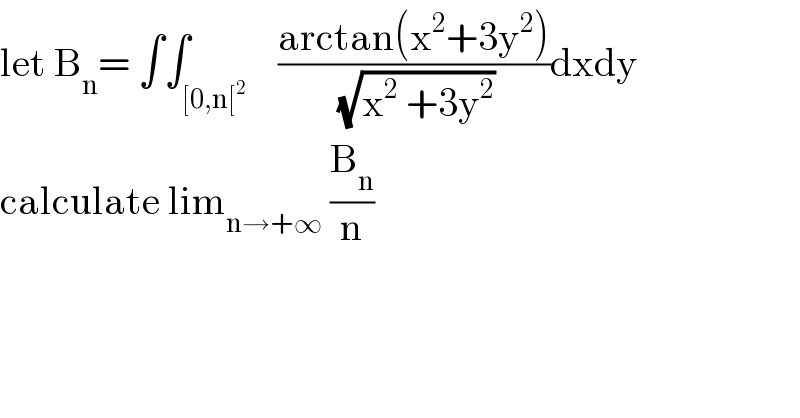 | ||
Answered by mathmax by abdo last updated on 26/Jul/20 | ||
 | ||
| ||
Commented by mathmax by abdo last updated on 26/Jul/20 | ||
![=(1/(2(√2))){ ln((√((r+(1/r)−(√2))/(r+(1/r)+(√2))))) +arctan((1/(√2))(r−(1/r))) +c ⇒ ∫_0 ^(2n) arctan(r^2 )dr =[r arctan(r^2 )]_0 ^(2n) −(1/(√2))[{ln((√((r^2 +1−(√2)r)/(r^2 +1+(√2)r)))) +arctan((1/(√2))(r−(1/r)))]_0 ^(2n) =2n arctan(4n^2 )−(1/(√2)){ln((√((4n^2 +1−2(√2)n)/(4n^2 +1+2(√2)n))))+arctan((1/(√2))(2n−(1/(2n)))=u_n +(π/2)} ⇒B_n =(π/2)u_n ⇒(B_n /n) =(π/2)(u_n /n) =π arctan(4n^2 ) −(1/(n(√2))){ln(√((4n^2 +1−2(√2)n)/(4n^2 +1+2(√2)n)))+arctan((1/(√2))(2n−(1/n))} ⇒lim_(n→+∞) (B_n /n) =π×(π/2) =(π^2 /2)](Q105172.png) | ||