Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 10485 by Saham last updated on 13/Feb/17

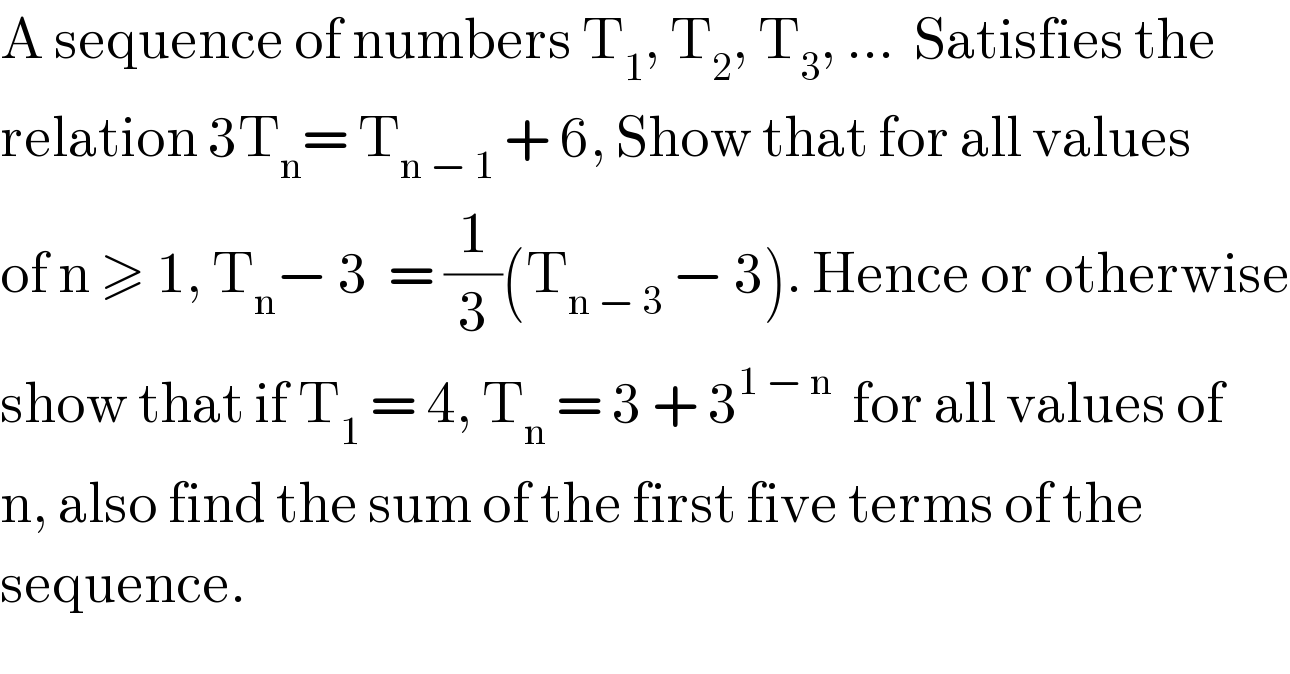
A sequence of numbers T_1 , T_2 , T_3 , ... Satisfies the relation 3T_n = T_(n − 1) + 6, Show that for all values of n ≥ 1, T_n − 3 = (1/3)(T_(n − 3) − 3). Hence or otherwise show that if T_1 = 4, T_n = 3 + 3^(1 − n) for all values of n, also find the sum of the first five terms of the sequence.

$$\mathrm{A}\:\mathrm{sequence}\:\mathrm{of}\:\mathrm{numbers}\:\mathrm{T}_{\mathrm{1}} ,\:\mathrm{T}_{\mathrm{2}} ,\:\mathrm{T}_{\mathrm{3}} ,\:...\:\:\mathrm{Satisfies}\:\mathrm{the} \\ $$$$\mathrm{relation}\:\mathrm{3T}_{\mathrm{n}} =\:\mathrm{T}_{\mathrm{n}\:−\:\mathrm{1}} \:+\:\mathrm{6},\:\mathrm{Show}\:\mathrm{that}\:\mathrm{for}\:\mathrm{all}\:\mathrm{values}\: \\ $$$$\mathrm{of}\:\mathrm{n}\:\geqslant\:\mathrm{1},\:\mathrm{T}_{\mathrm{n}} −\:\mathrm{3}\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{T}_{\mathrm{n}\:−\:\mathrm{3}} \:−\:\mathrm{3}\right).\:\mathrm{Hence}\:\mathrm{or}\:\mathrm{otherwise} \\ $$$$\mathrm{show}\:\mathrm{that}\:\mathrm{if}\:\mathrm{T}_{\mathrm{1}} \:=\:\mathrm{4},\:\mathrm{T}_{\mathrm{n}} \:=\:\mathrm{3}\:+\:\mathrm{3}^{\mathrm{1}\:−\:\mathrm{n}} \:\:\mathrm{for}\:\mathrm{all}\:\mathrm{values}\:\mathrm{of} \\ $$$$\mathrm{n},\:\mathrm{also}\:\mathrm{find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{first}\:\mathrm{five}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\: \\ $$$$\mathrm{sequence}. \\ $$

Answered by mrW1 last updated on 19/Feb/17

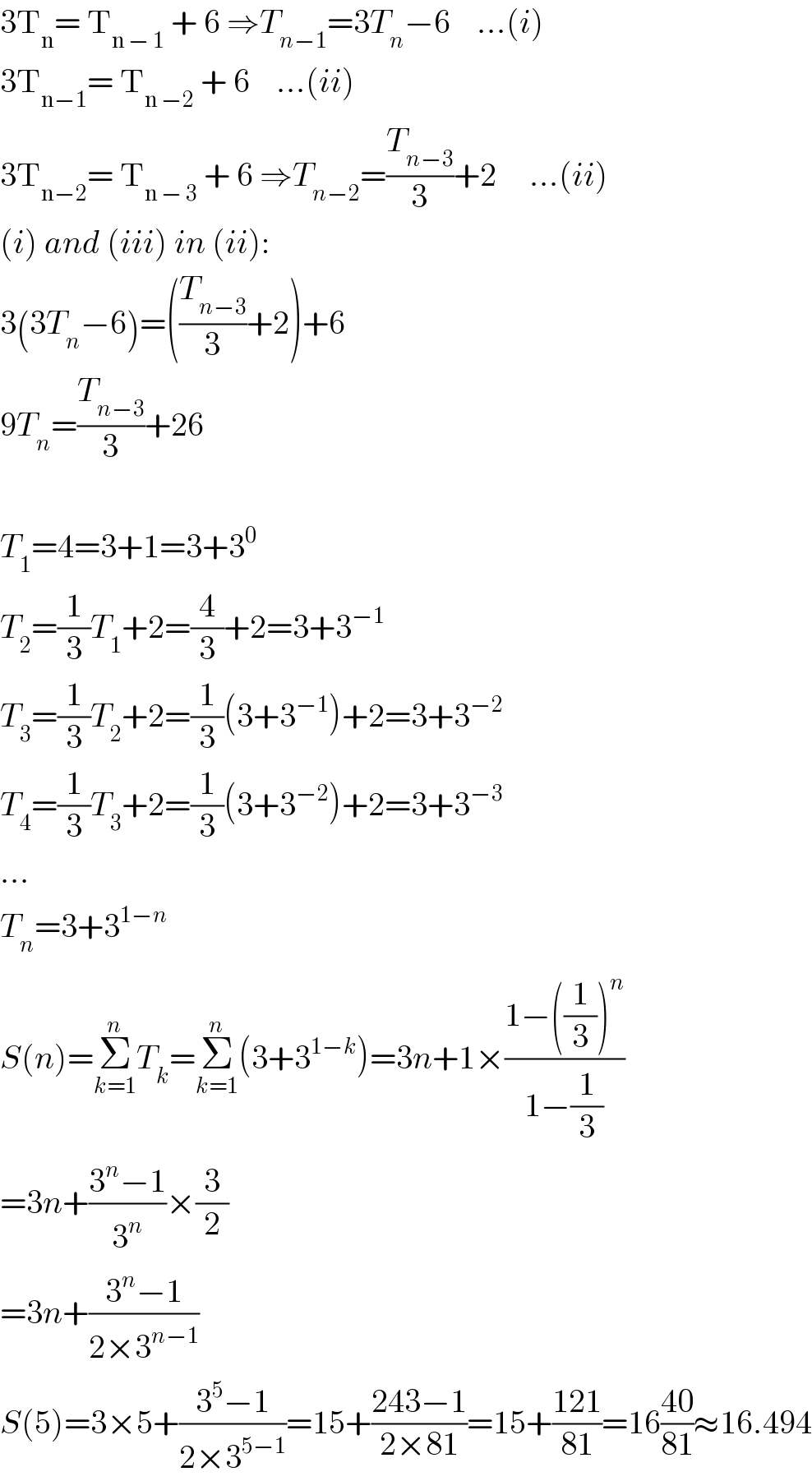
3T_n = T_(n − 1) + 6 ⇒T_(n−1) =3T_n −6 ...(i) 3T_(n−1) = T_(n −2) + 6 ...(ii) 3T_(n−2) = T_(n − 3) + 6 ⇒T_(n−2) =(T_(n−3) /3)+2 ...(ii) (i) and (iii) in (ii): 3(3T_n −6)=((T_(n−3) /3)+2)+6 9T_n =(T_(n−3) /3)+26 T_1 =4=3+1=3+3^0 T_2 =(1/3)T_1 +2=(4/3)+2=3+3^(−1) T_3 =(1/3)T_2 +2=(1/3)(3+3^(−1) )+2=3+3^(−2) T_4 =(1/3)T_3 +2=(1/3)(3+3^(−2) )+2=3+3^(−3) ... T_n =3+3^(1−n) S(n)=Σ_(k=1) ^n T_k =Σ_(k=1) ^n (3+3^(1−k) )=3n+1×((1−((1/3))^n )/(1−(1/3))) =3n+((3^n −1)/3^n )×(3/2) =3n+((3^n −1)/(2×3^(n−1) )) S(5)=3×5+((3^5 −1)/(2×3^(5−1) ))=15+((243−1)/(2×81))=15+((121)/(81))=16((40)/(81))≈16.494

$$\mathrm{3T}_{\mathrm{n}} =\:\mathrm{T}_{\mathrm{n}\:−\:\mathrm{1}} \:+\:\mathrm{6}\:\Rightarrow{T}_{{n}−\mathrm{1}} =\mathrm{3}{T}_{{n}} −\mathrm{6}\:\:\:\:...\left({i}\right) \\ $$$$\mathrm{3T}_{\mathrm{n}−\mathrm{1}} =\:\mathrm{T}_{\mathrm{n}\:−\mathrm{2}} \:+\:\mathrm{6}\:\:\:\:...\left({ii}\right) \\ $$$$\mathrm{3T}_{\mathrm{n}−\mathrm{2}} =\:\mathrm{T}_{\mathrm{n}\:−\:\mathrm{3}} \:+\:\mathrm{6}\:\Rightarrow{T}_{{n}−\mathrm{2}} =\frac{{T}_{{n}−\mathrm{3}} }{\mathrm{3}}+\mathrm{2}\:\:\:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)\:{and}\:\left({iii}\right)\:{in}\:\left({ii}\right): \\ $$$$\mathrm{3}\left(\mathrm{3}{T}_{{n}} −\mathrm{6}\right)=\left(\frac{{T}_{{n}−\mathrm{3}} }{\mathrm{3}}+\mathrm{2}\right)+\mathrm{6} \\ $$$$\mathrm{9}{T}_{{n}} =\frac{{T}_{{n}−\mathrm{3}} }{\mathrm{3}}+\mathrm{26} \\ $$$$ \\ $$$${T}_{\mathrm{1}} =\mathrm{4}=\mathrm{3}+\mathrm{1}=\mathrm{3}+\mathrm{3}^{\mathrm{0}} \\ $$$${T}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}}{T}_{\mathrm{1}} +\mathrm{2}=\frac{\mathrm{4}}{\mathrm{3}}+\mathrm{2}=\mathrm{3}+\mathrm{3}^{−\mathrm{1}} \\ $$$${T}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{3}}{T}_{\mathrm{2}} +\mathrm{2}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{3}+\mathrm{3}^{−\mathrm{1}} \right)+\mathrm{2}=\mathrm{3}+\mathrm{3}^{−\mathrm{2}} \\ $$$${T}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{3}}{T}_{\mathrm{3}} +\mathrm{2}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{3}+\mathrm{3}^{−\mathrm{2}} \right)+\mathrm{2}=\mathrm{3}+\mathrm{3}^{−\mathrm{3}} \\ $$$$... \\ $$$${T}_{{n}} =\mathrm{3}+\mathrm{3}^{\mathrm{1}−{n}} \\ $$$${S}\left({n}\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{T}_{{k}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{3}+\mathrm{3}^{\mathrm{1}−{k}} \right)=\mathrm{3}{n}+\mathrm{1}×\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} }{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$=\mathrm{3}{n}+\frac{\mathrm{3}^{{n}} −\mathrm{1}}{\mathrm{3}^{{n}} }×\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$=\mathrm{3}{n}+\frac{\mathrm{3}^{{n}} −\mathrm{1}}{\mathrm{2}×\mathrm{3}^{{n}−\mathrm{1}} } \\ $$$${S}\left(\mathrm{5}\right)=\mathrm{3}×\mathrm{5}+\frac{\mathrm{3}^{\mathrm{5}} −\mathrm{1}}{\mathrm{2}×\mathrm{3}^{\mathrm{5}−\mathrm{1}} }=\mathrm{15}+\frac{\mathrm{243}−\mathrm{1}}{\mathrm{2}×\mathrm{81}}=\mathrm{15}+\frac{\mathrm{121}}{\mathrm{81}}=\mathrm{16}\frac{\mathrm{40}}{\mathrm{81}}\approx\mathrm{16}.\mathrm{494} \\ $$

Commented by Saham last updated on 19/Feb/17

God bless you sir. i will reduce it.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{will}\:\mathrm{reduce}\:\mathrm{it}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com