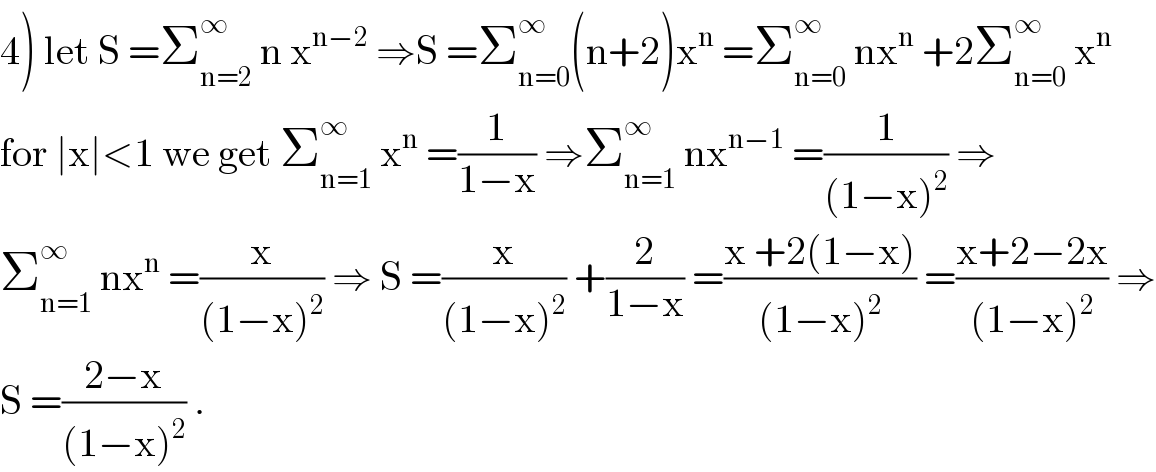Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 104871 by I want to learn more last updated on 24/Jul/20

Answered by mathmax by abdo last updated on 24/Jul/20

A_p =∫_0 ^1 ((tan^2 x)/x^p )dx ⇒A_p =∫_0 ^1 (((tanx)/x))^2 ×(dx/x^(p−2) ) the function x→(((tanx)/x))^2 ×(1/x^(p−2) ) is continue on]0,1] so integrable at V(o) f(x) ∼(1/x^(p−2) ) and ∫ (dx/x^(p−2) ) converge ⇔ p−2<1 ⇔p<3

$$\mathrm{A}_{\mathrm{p}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{p}} }\mathrm{dx}\:\Rightarrow\mathrm{A}_{\mathrm{p}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\frac{\mathrm{tanx}}{\mathrm{x}}\right)^{\mathrm{2}} \:×\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{p}−\mathrm{2}} } \\ $$$$\left.\mathrm{t}\left.\mathrm{he}\:\mathrm{function}\:\mathrm{x}\rightarrow\left(\frac{\mathrm{tanx}}{\mathrm{x}}\right)^{\mathrm{2}} ×\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{p}−\mathrm{2}} }\:\mathrm{is}\:\mathrm{continue}\:\mathrm{on}\right]\mathrm{0},\mathrm{1}\right]\:\mathrm{so}\:\mathrm{integrable} \\ $$$$\mathrm{at}\:\mathrm{V}\left(\mathrm{o}\right)\:\mathrm{f}\left(\mathrm{x}\right)\:\sim\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{p}−\mathrm{2}} }\:\mathrm{and}\:\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{p}−\mathrm{2}} }\:\mathrm{converge}\:\Leftrightarrow\:\mathrm{p}−\mathrm{2}<\mathrm{1}\:\Leftrightarrow\mathrm{p}<\mathrm{3} \\ $$

Commented by I want to learn more last updated on 24/Jul/20

Thanks sir. I appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Commented by mathmax by abdo last updated on 24/Jul/20

you are welcome sir.

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$

Answered by mathmax by abdo last updated on 24/Jul/20

4) let S =Σ_(n=2) ^∞ n x^(n−2) ⇒S =Σ_(n=0) ^∞ (n+2)x^n =Σ_(n=0) ^∞ nx^n +2Σ_(n=0) ^∞ x^n for ∣x∣<1 we get Σ_(n=1) ^∞ x^n =(1/(1−x)) ⇒Σ_(n=1) ^∞ nx^(n−1) =(1/((1−x)^2 )) ⇒ Σ_(n=1) ^∞ nx^n =(x/((1−x)^2 )) ⇒ S =(x/((1−x)^2 )) +(2/(1−x)) =((x +2(1−x))/((1−x)^2 )) =((x+2−2x)/((1−x)^2 )) ⇒ S =((2−x)/((1−x)^2 )) .

$$\left.\mathrm{4}\right)\:\mathrm{let}\:\mathrm{S}\:=\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\mathrm{n}\:\mathrm{x}^{\mathrm{n}−\mathrm{2}} \:\Rightarrow\mathrm{S}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(\mathrm{n}+\mathrm{2}\right)\mathrm{x}^{\mathrm{n}} \:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}} \:+\mathrm{2}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \\ $$$$\mathrm{for}\:\mid\mathrm{x}\mid<\mathrm{1}\:\mathrm{we}\:\mathrm{get}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\:\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \:=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}} \:=\frac{\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:\Rightarrow\:\mathrm{S}\:=\frac{\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:+\frac{\mathrm{2}}{\mathrm{1}−\mathrm{x}}\:=\frac{\mathrm{x}\:+\mathrm{2}\left(\mathrm{1}−\mathrm{x}\right)}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:=\frac{\mathrm{x}+\mathrm{2}−\mathrm{2x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{S}\:=\frac{\mathrm{2}−\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com