Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 10489 by Saham last updated on 13/Feb/17

The fifth, nineth, sixteenth terms of a linear sequence are consecutive terms of an exponential sequence . (1) Find the common difference of the linear sequence in terms of the first term (2) Show that 21^(th) , 37^(th) , 65^(th) terms of the linear sequence are consecutive terms of an exponential sequence whose common ratio is (3/4)

$$\mathrm{The}\:\mathrm{fifth},\:\mathrm{nineth},\:\mathrm{sixteenth}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{a}\:\mathrm{linear}\: \\ $$$$\mathrm{sequence}\:\mathrm{are}\:\mathrm{consecutive}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{an}\:\mathrm{exponential} \\ $$$$\mathrm{sequence}\:. \\ $$$$\left(\mathrm{1}\right)\:\mathrm{Find}\:\mathrm{the}\:\mathrm{common}\:\mathrm{difference}\:\mathrm{of}\:\mathrm{the}\:\mathrm{linear}\: \\ $$$$\mathrm{sequence}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{first}\:\mathrm{term} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{Show}\:\mathrm{that}\:\mathrm{21}^{\mathrm{th}} ,\:\mathrm{37}^{\mathrm{th}} ,\:\mathrm{65}^{\mathrm{th}} \:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{linear} \\ $$$$\mathrm{sequence}\:\mathrm{are}\:\mathrm{consecutive}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{an}\:\mathrm{exponential} \\ $$$$\mathrm{sequence}\:\mathrm{whose}\:\mathrm{common}\:\mathrm{ratio}\:\mathrm{is}\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$

Answered by mrW1 last updated on 14/Feb/17

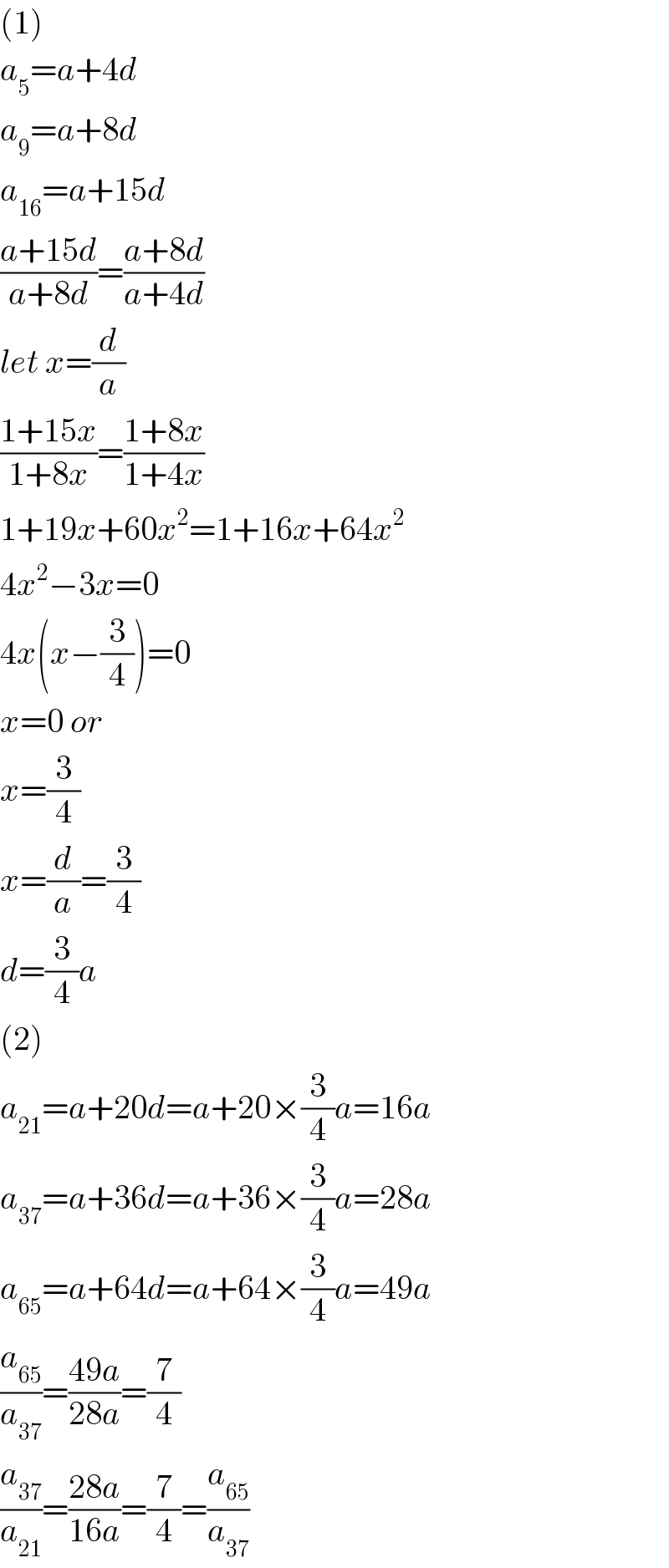
(1) a_5 =a+4d a_9 =a+8d a_(16) =a+15d ((a+15d)/(a+8d))=((a+8d)/(a+4d)) let x=(d/a) ((1+15x)/(1+8x))=((1+8x)/(1+4x)) 1+19x+60x^2 =1+16x+64x^2 4x^2 −3x=0 4x(x−(3/4))=0 x=0 or x=(3/4) x=(d/a)=(3/4) d=(3/4)a (2) a_(21) =a+20d=a+20×(3/4)a=16a a_(37) =a+36d=a+36×(3/4)a=28a a_(65) =a+64d=a+64×(3/4)a=49a (a_(65) /a_(37) )=((49a)/(28a))=(7/4) (a_(37) /a_(21) )=((28a)/(16a))=(7/4)=(a_(65) /a_(37) )

$$\left(\mathrm{1}\right) \\ $$$${a}_{\mathrm{5}} ={a}+\mathrm{4}{d} \\ $$$${a}_{\mathrm{9}} ={a}+\mathrm{8}{d} \\ $$$${a}_{\mathrm{16}} ={a}+\mathrm{15}{d} \\ $$$$\frac{{a}+\mathrm{15}{d}}{{a}+\mathrm{8}{d}}=\frac{{a}+\mathrm{8}{d}}{{a}+\mathrm{4}{d}} \\ $$$${let}\:{x}=\frac{{d}}{{a}} \\ $$$$\frac{\mathrm{1}+\mathrm{15}{x}}{\mathrm{1}+\mathrm{8}{x}}=\frac{\mathrm{1}+\mathrm{8}{x}}{\mathrm{1}+\mathrm{4}{x}} \\ $$$$\mathrm{1}+\mathrm{19}{x}+\mathrm{60}{x}^{\mathrm{2}} =\mathrm{1}+\mathrm{16}{x}+\mathrm{64}{x}^{\mathrm{2}} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{3}{x}=\mathrm{0} \\ $$$$\mathrm{4}{x}\left({x}−\frac{\mathrm{3}}{\mathrm{4}}\right)=\mathrm{0} \\ $$$${x}=\mathrm{0}\:{or} \\ $$$${x}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${x}=\frac{{d}}{{a}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${d}=\frac{\mathrm{3}}{\mathrm{4}}{a} \\ $$$$\left(\mathrm{2}\right) \\ $$$${a}_{\mathrm{21}} ={a}+\mathrm{20}{d}={a}+\mathrm{20}×\frac{\mathrm{3}}{\mathrm{4}}{a}=\mathrm{16}{a} \\ $$$${a}_{\mathrm{37}} ={a}+\mathrm{36}{d}={a}+\mathrm{36}×\frac{\mathrm{3}}{\mathrm{4}}{a}=\mathrm{28}{a} \\ $$$${a}_{\mathrm{65}} ={a}+\mathrm{64}{d}={a}+\mathrm{64}×\frac{\mathrm{3}}{\mathrm{4}}{a}=\mathrm{49}{a} \\ $$$$\frac{{a}_{\mathrm{65}} }{{a}_{\mathrm{37}} }=\frac{\mathrm{49}{a}}{\mathrm{28}{a}}=\frac{\mathrm{7}}{\mathrm{4}} \\ $$$$\frac{{a}_{\mathrm{37}} }{{a}_{\mathrm{21}} }=\frac{\mathrm{28}{a}}{\mathrm{16}{a}}=\frac{\mathrm{7}}{\mathrm{4}}=\frac{{a}_{\mathrm{65}} }{{a}_{\mathrm{37}} } \\ $$

Commented by Saham last updated on 14/Feb/17

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com