
Question and Answers Forum
Question Number 104904 by bemath last updated on 24/Jul/20
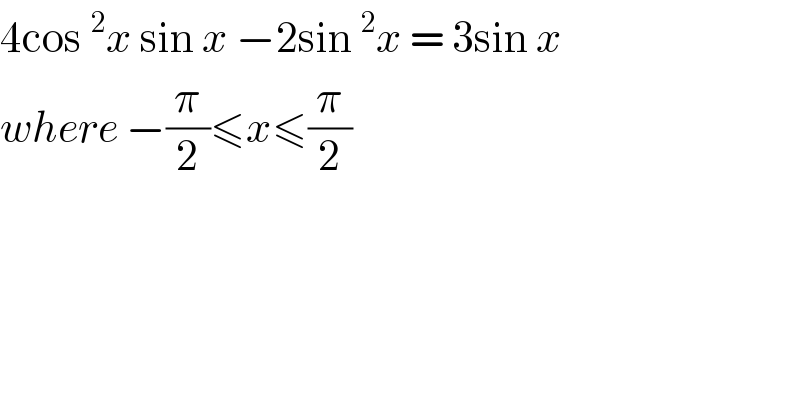
Answered by bramlex last updated on 24/Jul/20
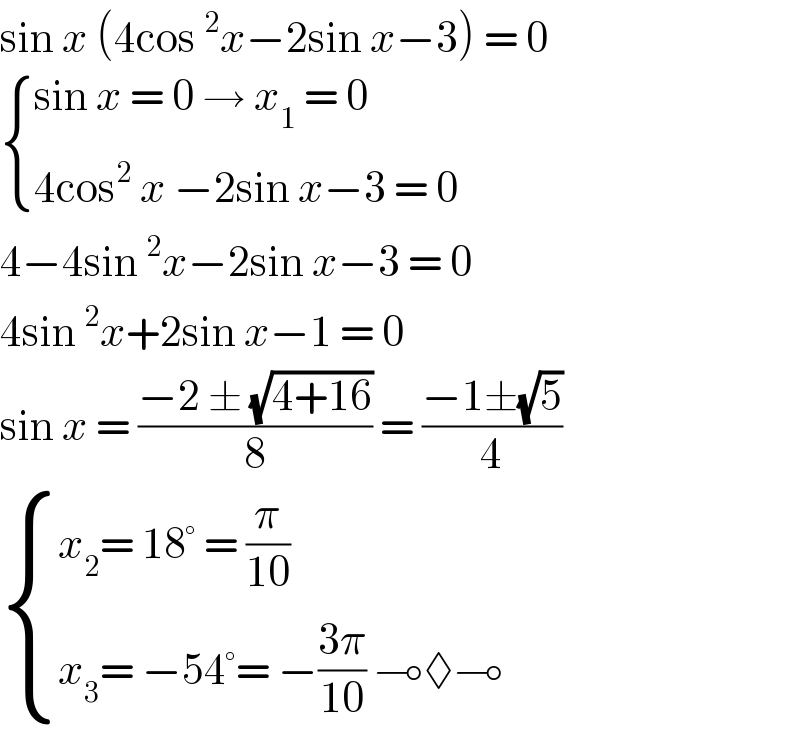
Answered by Dwaipayan Shikari last updated on 24/Jul/20

Answered by 1549442205PVT last updated on 24/Jul/20
![⇔sinx(4cos^(2 ) x−2sinx−3)=0 ⇔sinx[(4(1−sin^(2 ) x)−2sinx−3]=0 ⇔sinx(4sin^2 x+2sinx−1)=0 i)sinx=0⇔x=kπ .Since x∈[−(π/2),(π/2)] ⇒x=0 ii)4sin^2 x+2sinx−1=0 ⇔sinx =((−1+(√5))/4) or sinx=((−1−(√5))/4) a)sinx=(((√5)−1)/4)=sin(π/(10))⇒x=(π/(10)) b)sinx=((−((√5)+1))/4)=sin((−3π)/(10))⇒x=((−3π)/(10)) Thus,x∈{0,(π/(10)),((−3π)/(10))}](Q104915.png)
| ||
Question and Answers Forum | ||
Question Number 104904 by bemath last updated on 24/Jul/20 | ||
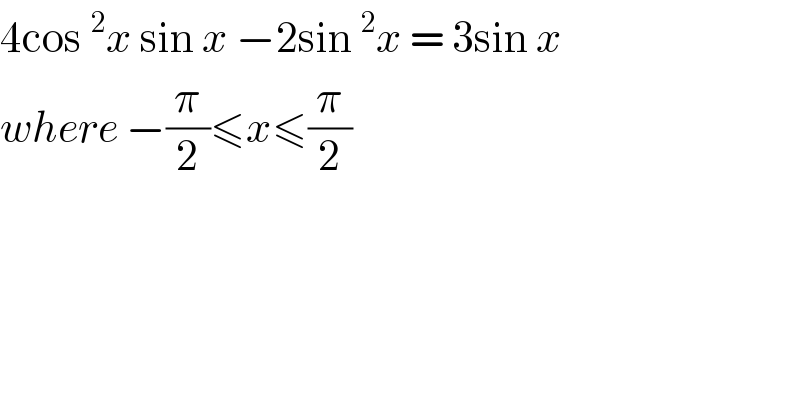 | ||
Answered by bramlex last updated on 24/Jul/20 | ||
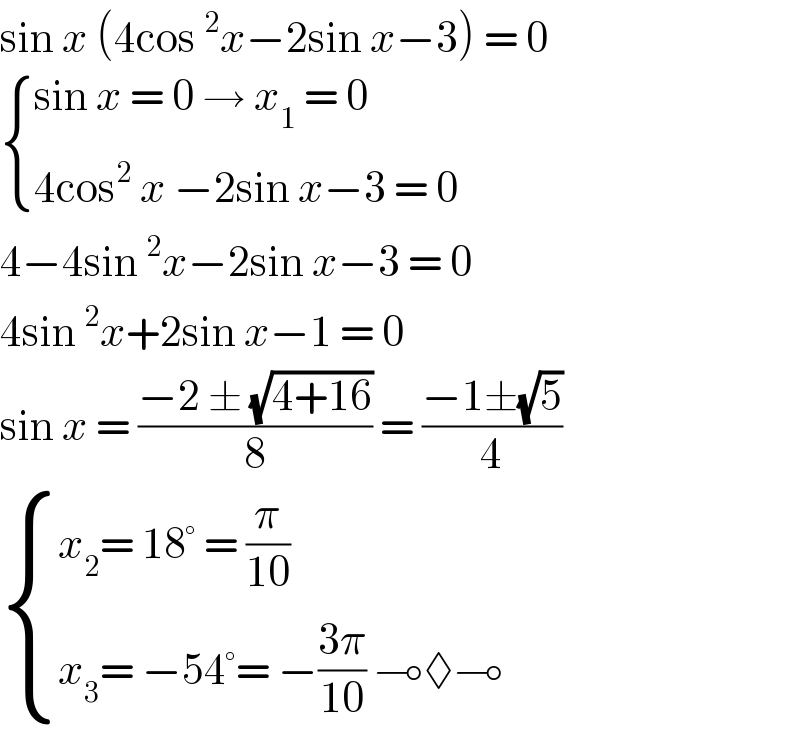 | ||
| ||
Answered by Dwaipayan Shikari last updated on 24/Jul/20 | ||
 | ||
| ||
Answered by 1549442205PVT last updated on 24/Jul/20 | ||
![⇔sinx(4cos^(2 ) x−2sinx−3)=0 ⇔sinx[(4(1−sin^(2 ) x)−2sinx−3]=0 ⇔sinx(4sin^2 x+2sinx−1)=0 i)sinx=0⇔x=kπ .Since x∈[−(π/2),(π/2)] ⇒x=0 ii)4sin^2 x+2sinx−1=0 ⇔sinx =((−1+(√5))/4) or sinx=((−1−(√5))/4) a)sinx=(((√5)−1)/4)=sin(π/(10))⇒x=(π/(10)) b)sinx=((−((√5)+1))/4)=sin((−3π)/(10))⇒x=((−3π)/(10)) Thus,x∈{0,(π/(10)),((−3π)/(10))}](Q104915.png) | ||
| ||