(1) ∫ (dx/(x^6 −64)) (2) y′ + y tan x = sin 2x y(0) = 1


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 105039 by bemath last updated on 25/Jul/20

$(1) \int \frac{d x}{x^{6} - 64}$ $(2) y^{'} + y \tan x = \sin 2 x$ $y (0) = 1$
	Answered by bobhans last updated on 25/Jul/20
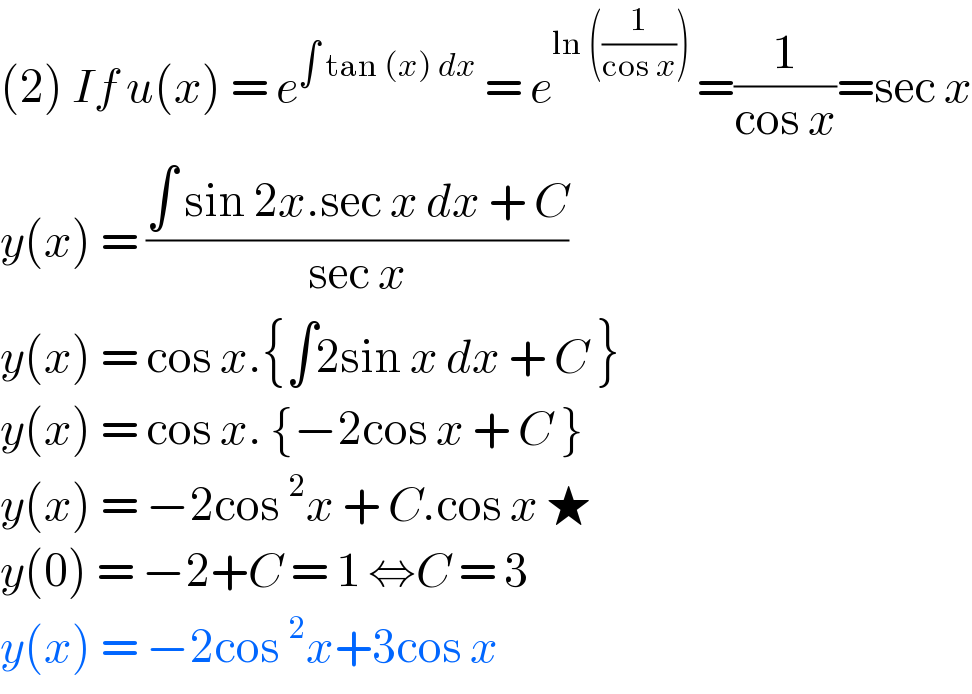
	$(2) If u(x) = e^(∫ tan (x) dx) = e^(ln ((1/(cos x))) ) =(1/(cos x))=sec x y(x) = ((∫ sin 2x.sec x dx + C)/(sec x)) y(x) = cos x.{∫2sin x dx + C } y(x) = cos x. {−2cos x + C } y(x) = −2cos^2 x + C.cos x ★ y(0) = −2+C = 1 ⇔C = 3 y(x) = −2cos^2 x+3cos x$
	$(2) I f u (x) = e^{\int \tan (x) d x} = e^{\ln (\frac{1}{\cos x})} = \frac{1}{\cos x} = \sec x$ $y (x) = \frac{\int \sin 2 x . \sec x d x + C}{\sec x}$ $y (x) = \cos x . {\int 2 \sin x d x + C}$ $y (x) = \cos x . {- 2 \cos x + C}$ $y (x) = - 2 \cos^{2} x + C . \cos x ★$ $y (0) = - 2 + C = 1 \Leftrightarrow C = 3$ $y (x) = - 2 \cos^{2} x + 3 \cos x$
	Answered by mathmax by abdo last updated on 25/Jul/20

	$1) complex method we decompose F (z) = \frac{1}{z^{6} - 64} \Rightarrow$ $z^{6} = 64 let z = {re}^{i θ} so e \Rightarrow r^{6} e^{i 6 θ} = 64 e^{i (2 k π)} \Rightarrow r =^{6} \sqrt{64} = 2$ $θ = \frac{k π}{3} and k \in [[0, 5]] so the roots are z_{k} = {2 e}^{i \frac{k π}{3}} and 0 ⩽ k ⩽ 5$ $\Rightarrow F (z) = \frac{1}{\prod_{k = 0}^{5} (z - z_{k})} = \sum_{k = 0}^{5} \frac{a_{k}}{z - z_{k}} with a_{k} = \frac{1}{{6 z}_{k}^{5}} = \frac{z_{k}}{6 (64)} = \frac{z_{k}}{384}$ $\Rightarrow F (z) = \frac{1}{384} \sum_{k = 0}^{5} \frac{z_{k}}{z - z_{k}} \Rightarrow \int F (z) dz = \frac{1}{384} \sum_{k = 0}^{5} z_{k} \int \frac{dz}{z - {2 e}^{\frac{ik π}{3}}}$ $= \frac{1}{384} \sum_{k = 0}^{5} ({2 e}^{\frac{ik π}{3}}) \ln (z - {2 e}^{\frac{ik π}{3}}) + C$
	Commented by Dwaipayan Shikari last updated on 25/Jul/20

	$I t h i n k i t c a n b e d o n e w i t h \frac{1}{16} \int \frac{1}{x^{3} - 8} - \int \frac{1}{x^{3} + 8}$ $= \frac{1}{16} \int \frac{A}{x - 2} + \frac{B x + C}{x^{2} + 2 x + 4} - \frac{1}{16} \int \frac{A^{'}}{x + 2} + \frac{B^{'} x + C^{'}}{x^{2} - 2 x + 4}$
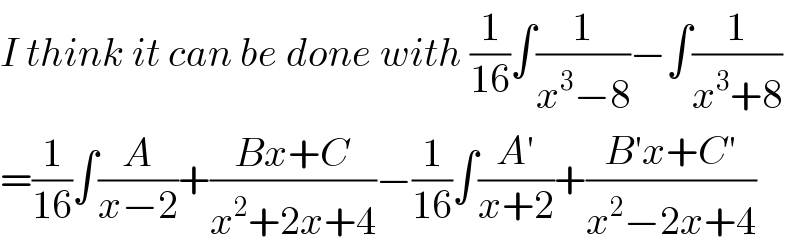
	Commented by mathmax by abdo last updated on 26/Jul/20

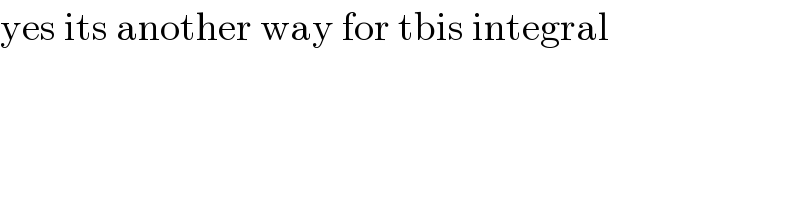
	$yes its another way for tbis integral$
	Answered by mathmax by abdo last updated on 25/Jul/20
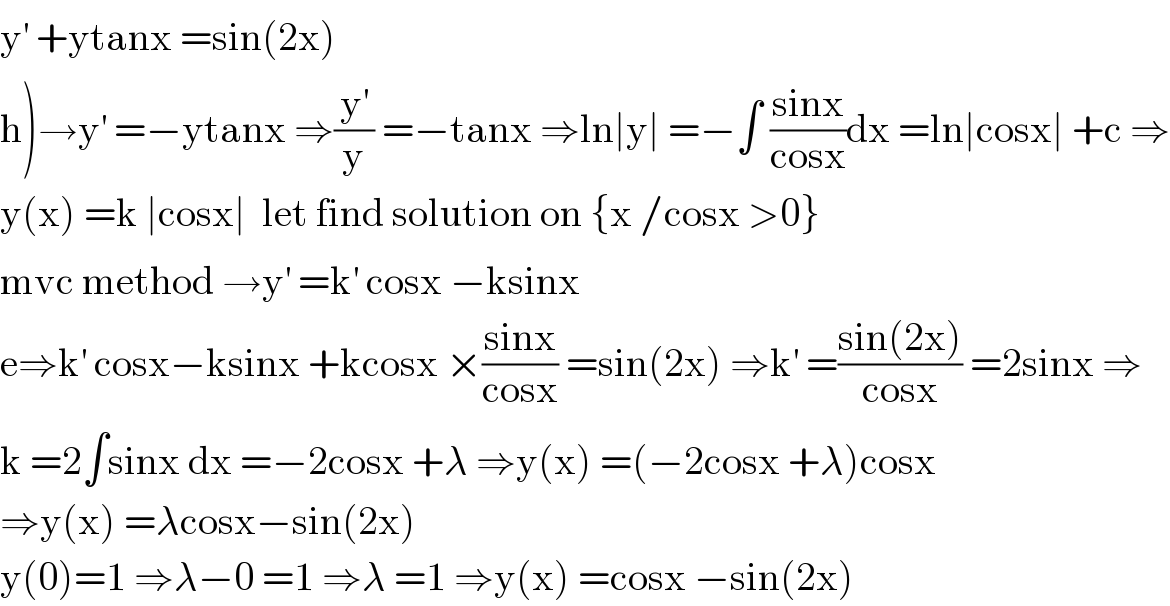
	$y^′ +ytanx =sin(2x) h)→y^′ =−ytanx ⇒(y^′ /y) =−tanx ⇒ln∣y∣ =−∫ ((sinx)/(cosx))dx =ln∣cosx∣ +c ⇒ y(x) =k ∣cosx∣ let find solution on {x /cosx >0} mvc method →y^′ =k^′ cosx −ksinx e⇒k^′ cosx−ksinx +kcosx ×((sinx)/(cosx)) =sin(2x) ⇒k^′ =((sin(2x))/(cosx)) =2sinx ⇒ k =2∫sinx dx =−2cosx +λ ⇒y(x) =(−2cosx +λ)cosx ⇒y(x) =λcosx−sin(2x) y(0)=1 ⇒λ−0 =1 ⇒λ =1 ⇒y(x) =cosx −sin(2x)$
	$y^{^{'}} + ytanx = \sin (2 x)$ $h) \to y^{^{'}} = - ytanx \Rightarrow \frac{y^{^{'}}}{y} = - tanx \Rightarrow \ln ∣ y ∣ = - \int \frac{sinx}{cosx} dx = \ln ∣ cosx ∣ + c \Rightarrow$ $y (x) = k ∣ cosx ∣ let find solution on {x / cosx > 0}$ $mvc method \to y^{^{'}} = k^{^{'}} cosx - ksinx$ $e \Rightarrow k^{^{'}} cosx - ksinx + kcosx \times \frac{sinx}{cosx} = \sin (2 x) \Rightarrow k^{^{'}} = \frac{\sin (2 x)}{cosx} = 2 sinx \Rightarrow$ $k = 2 \int sinx dx = - 2 cosx + λ \Rightarrow y (x) = (- 2 cosx + λ) cosx$ $\Rightarrow y (x) = λ cosx - \sin (2 x)$ $y (0) = 1 \Rightarrow λ - 0 = 1 \Rightarrow λ = 1 \Rightarrow y (x) = cosx - \sin (2 x)$
	Answered by Dwaipayan Shikari last updated on 25/Jul/20

	$\frac{d y}{d x} + y t a n x = s i n 2 x$ $I . F = e^{\int t a n x d x} = e^{l o g (s e c x)} = s e c x$ $y . s e c x = \int s i n 2 x s e c x d x = 2 \int s i n x = - 2 c o s x + C$ $y = - 2 {c o s}^{2} x + C c o s x$ $y (x) = - 2 {c o s}^{2} x + C c o s x$ $y (0) = - 2 + C$ $C = 3$ $y (x) = - 2 {c o s}^{2} x + 3 c o s x ★$
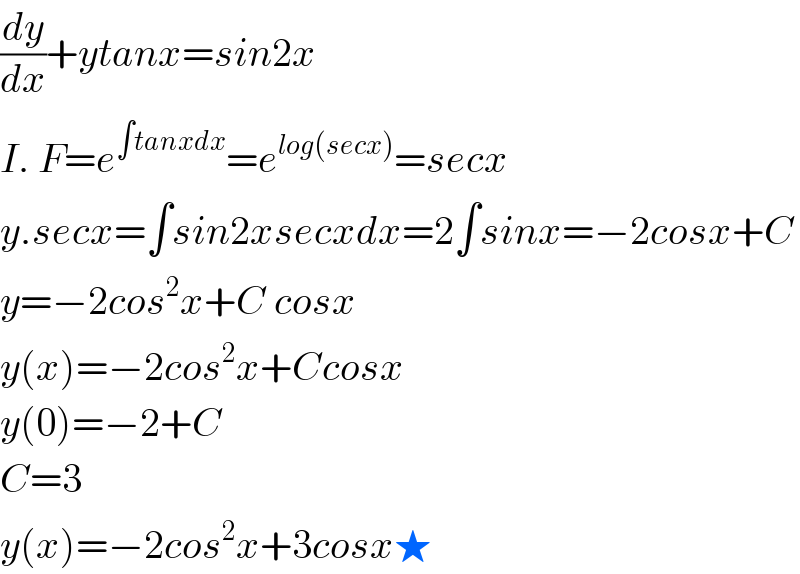
	Answered by OlafThorendsen last updated on 25/Jul/20

	$(1) R (x) = \frac{1}{x^{6} - 1}$ $R (x) = \frac{1}{(x - 1) (x + 1) (x^{2} - x + 1) (x^{2} - x + 1)}$ $\int R (x) d x =$ $\int (\frac{1}{6 (x - 1)} - \frac{1}{6 (x + 1)} + \frac{x - 2}{6 (x^{2} - x + 1)} - \frac{x + 2}{6 (x^{2} + x + 1)}) d x$ $= \frac{1}{6} \ln ∣ \frac{x - 1}{x + 1} ∣$ $+ \frac{1}{12} \int \frac{2 x - 1}{x^{2} - x + 1} d x - \frac{1}{12} \int \frac{2 x + 1}{x^{2} + x + 1} d x$ $- \frac{1}{4} \int \frac{d x}{x^{2} - x + 1} - \frac{1}{4} \int \frac{d x}{x^{2} + x + 1}$ $= \frac{1}{6} \ln ∣ \frac{x - 1}{x + 1} ∣ + \frac{1}{12} \ln ∣ \frac{x^{2} - x + 1}{x^{2} + x + 1} ∣$ $- \frac{1}{3} \int \frac{d x}{\frac{4}{3} {(x - \frac{1}{2})}^{2} + 1} - \frac{1}{3} \int \frac{d x}{\frac{4}{3} {(x + \frac{1}{2})}^{2} + 1}$ $= \frac{1}{6} \ln ∣ \frac{x - 1}{x + 1} ∣ + \frac{1}{12} \ln ∣ \frac{x^{2} - x + 1}{x^{2} + x + 1} ∣$ $- \frac{1}{2 \sqrt{3}} \arctan [\frac{2}{\sqrt{3}} (x - \frac{1}{2})] - \frac{1}{2 \sqrt{3}} \arctan [\frac{2}{\sqrt{3}} (x + \frac{1}{2})]$ $\arctan u + \arctan v = \arctan \frac{u + v}{1 - u v}$ $u = \frac{2}{\sqrt{3}} (x - \frac{1}{2}) and v = \frac{2}{\sqrt{3}} (x + \frac{1}{2})$ $\frac{u + v}{1 - u v} = \frac{\frac{4}{\sqrt{3}} x}{1 - \frac{4}{3} (x^{2} - \frac{1}{4})} = \frac{\sqrt{3} x}{1 - x^{2}}$ $Finally :$ $\int R (x) d x = \frac{1}{6} \ln ∣ \frac{x - 1}{x + 1} ∣ + \frac{1}{12} \ln ∣ \frac{x^{2} - x + 1}{x^{2} + x + 1} ∣ - \frac{1}{2 \sqrt{3}} \arctan \frac{\sqrt{3} x}{1 - x^{2}} + C$
	Commented by bemath last updated on 27/Jul/20

	$t h e q u e s t i o n \int \frac{d x}{x^{6} - 64} s i r$
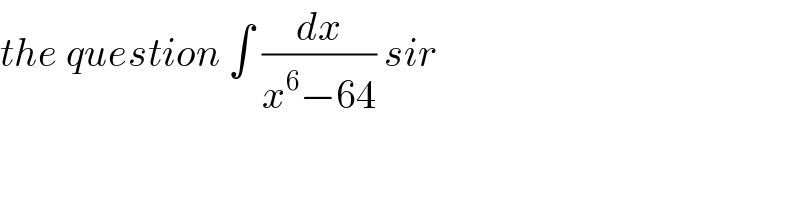
	Answered by OlafThorendsen last updated on 25/Jul/20

	$Q 2 .$ $y^{'} \cos x - (- y \sin x) = \cos x \sin 2 x = {2 \cos}^{2} x \sin x$ $\frac{y^{'} \cos x - (- y \sin x)}{\cos^{2} x} = 2 \sin x$ $\frac{d}{d x} (\frac{y}{\cos x}) = 2 \sin x$ $\frac{y}{\cos x} = - 2 \cos x + C$ $y = - {2 \cos}^{2} x + Ccos x$ $y (0) = - 2 + C = 1 \Rightarrow C = 3$ $y = 3 \cos x - {2 \cos}^{2} x$
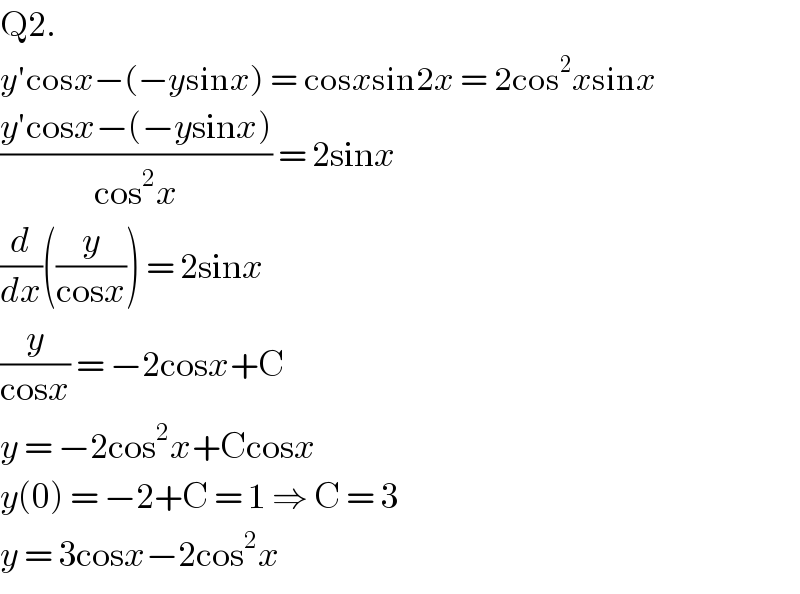
	Answered by bramlex last updated on 26/Jul/20

	$(1) \int \frac{d x}{x^{6} - {(2)}^{6}} = \frac{1}{24} \ln (\frac{{(x - 2)}^{2} (x^{2} - 2 x + 4)}{{(x + 2)}^{2} (x^{2} + 2 x + 4)}) - \frac{1}{4 \sqrt{3}} \tan^{- 1} (\frac{2}{x^{2} + 2}) + C$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum