Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 105205 by Ar Brandon last updated on 26/Jul/20

Commented by Aziztisffola last updated on 26/Jul/20

$$\mathrm{ce}{\mathrm{n}}^{\prime }\mathrm{est}\mathrm{pas}\mathrm{tres}\mathrm{lisible}.$$

Commented by Ar Brandon last updated on 26/Jul/20

D'accord, désolé pour l'inconvenance.

Answered by mathmax by abdo last updated on 27/Jul/20

$${\mathrm{u}}_{\mathrm{n}}=\frac{3}{4}{\mathrm{u}}_{\mathrm{n}-1}+\frac{1}{4}{\mathrm{u}}_{\mathrm{n}-2}\Rightarrow {4\mathrm{u}}_{\mathrm{n}}={3\mathrm{u}}_{\mathrm{n}-1}+{\mathrm{u}}_{\mathrm{n}-2}\Rightarrow {4\mathrm{u}}_{\mathrm{n}+2}={3\mathrm{u}}_{\mathrm{n}+1}+{\mathrm{u}}_{\mathrm{n}}\Rightarrow$$$${4\mathrm{u}}_{\mathrm{n}+2}-{3\mathrm{u}}_{\mathrm{n}+1}-{\mathrm{u}}_{\mathrm{n}}=0\to {4\mathrm{r}}^2-3\mathrm{r}-1=0$$$$\mathrm{\Delta }=9-4(-4)=25\Rightarrow {\mathrm{r}}_1=\frac{3+5}{8}=1\mathrm{and}{\mathrm{r}}_2=\frac{3-5}{8}=-\frac{1}{4}\Rightarrow$$$${\mathrm{u}}_{\mathrm{n}}=\alpha +\beta {(-\frac{1}{4})}^{\mathrm{n}}$$$${\mathrm{u}}_0=\alpha +\beta$$$${\mathrm{u}}_1=\alpha -\frac{\beta }{4}\Rightarrow \frac{5}{4}\beta ={\mathrm{u}}_0-{\mathrm{u}}_1\Rightarrow \beta =\frac{4}{5}({\mathrm{u}}_0-{\mathrm{u}}_1)$$$$\alpha ={\mathrm{u}}_0-\beta ={\mathrm{u}}_0-\frac{4}{5}({\mathrm{u}}_{\mathrm{o}}-{\mathrm{u}}_1)=\frac{1}{5}{\mathrm{u}}_0+\frac{4}{5}{\mathrm{u}}_1$$$$\Rightarrow {\mathrm{u}}_{\mathrm{n}}=\frac{1}{5}({\mathrm{u}}_0+{4\mathrm{u}}_1)+\frac{4}{5}({\mathrm{u}}_0-{\mathrm{u}}_1){(-\frac{1}{4})}^{\mathrm{n}}$$$$\mathrm{if}{\mathrm{u}}_0={\mathrm{u}}_1\Rightarrow {\mathrm{u}}_{\mathrm{n}}={\mathrm{u}}_0\mathrm{\forall }\mathrm{n}\mathrm{so}{\mathrm{u}}_{\mathrm{n}}\mathrm{is}\mathrm{constante}$$$$2){\mathrm{v}}_{\mathrm{n}}={\mathrm{u}}_{\mathrm{n}}-{\mathrm{u}}_{\mathrm{n}-1}\Rightarrow {\mathrm{v}}_{\mathrm{n}+1}={\mathrm{u}}_{\mathrm{n}+1}-{\mathrm{u}}_{\mathrm{n}}=\frac{3}{4}{\mathrm{u}}_{\mathrm{n}}+\frac{1}{4}{\mathrm{u}}_{\mathrm{n}-1}-{\mathrm{u}}_{\mathrm{n}-1}$$$$=\frac{3}{4}{\mathrm{u}}_{\mathrm{n}}-\frac{3}{4}{\mathrm{u}}_{\mathrm{n}-1}=\frac{3}{4}({\mathrm{u}}_{\mathrm{n}}-{\mathrm{u}}_{\mathrm{n}-1})=\frac{3}{4}{\mathrm{v}}_{\mathrm{n}}\Rightarrow {\mathrm{v}}_{\mathrm{n}}\mathrm{is}\mathrm{geometric}\mathrm{with}$$$$\mathrm{q}=\frac{3}{4}\Rightarrow {\mathrm{v}}_{\mathrm{n}}={\mathrm{v}}_1\times {\left(\frac{3}{4}\right)}^{\mathrm{n}-1}$$$${\mathrm{v}}_1={\mathrm{u}}_1-{\mathrm{u}}_0\ne 0\Rightarrow {\mathrm{v}}_{\mathrm{n}}=({\mathrm{u}}_1-{\mathrm{u}}_0){\left(\frac{3}{4}\right)}^{\mathrm{n}-1}$$$$\sum _{\mathrm{k}=1}^{\mathrm{n}}{\mathrm{v}}_{\mathrm{k}}=\sum _{\mathrm{k}=1}^{\mathrm{n}}({\mathrm{u}}_{\mathrm{k}}-{\mathrm{u}}_{\mathrm{k}-1})={\mathrm{u}}_1-{\mathrm{u}}_0+{\mathrm{u}}_2-{\mathrm{u}}_1+...+{\mathrm{u}}_{\mathrm{n}}-{\mathrm{u}}_{\mathrm{n}-1}$$$$={\mathrm{u}}_{\mathrm{n}}-{\mathrm{u}}_{\mathrm{o}}\Rightarrow {\mathrm{u}}_{\mathrm{n}}-{\mathrm{u}}_0=({\mathrm{u}}_1-{\mathrm{u}}_0)\sum _{\mathrm{k}=1}^{\mathrm{n}}{\left(\frac{3}{4}\right)}^{\mathrm{k}-1}(\mathrm{k}-1=\mathrm{p})$$$$=({\mathrm{u}}_1-{\mathrm{u}}_0)\sum _{\mathrm{k}=0}^{\mathrm{n}-1}{\left(\frac{3}{4}\right)}^{\mathrm{p}}=({\mathrm{u}}_1-{\mathrm{u}}_0)\times \frac{1-{\left(\frac{3}{4}\right)}^{\mathrm{n}}}{1-\frac{3}{4}}$$$$=4({\mathrm{u}}_1-{\mathrm{u}}_0)\times (1-{\left(\frac{3}{4}\right)}^{\mathrm{n}})\Rightarrow {\mathrm{u}}_{\mathrm{n}}={\mathrm{u}}_0+4({\mathrm{u}}_1-{\mathrm{u}}_0)(1-{\left(\frac{3}{4}\right)}^{\mathrm{n}})$$

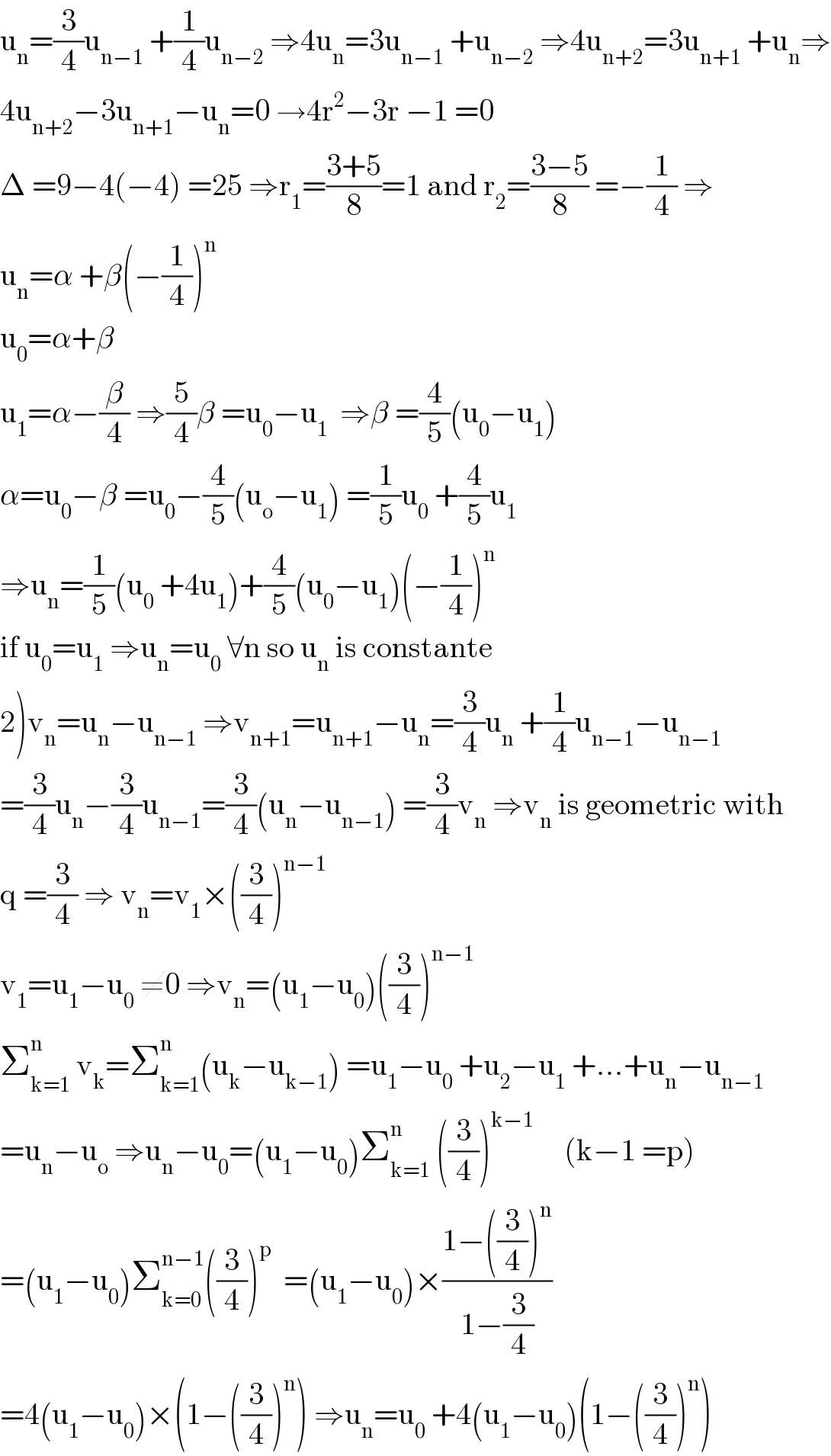
Commented by Ar Brandon last updated on 27/Jul/20

Thanks Sir. Always willing to help ! ��

Commented by abdomathmax last updated on 27/Jul/20

$$\mathrm{you}\mathrm{are}\mathrm{welcome}\mathrm{sir}.$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com